新人教版七年级下册8.2-加减消元法解二元一次方程组(共30张PPT)
文档属性
| 名称 | 新人教版七年级下册8.2-加减消元法解二元一次方程组(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 00:00:00 | ||
图片预览







文档简介
8.2.2解二元一次方程组—加减法
1、用代入法解方程的关键是什么?
2、解二元一次方程组的基本思路是什么?
回顾
一元
消元
转化
二元
消元:
二元
一元
主要步骤:
基本思路:
4、写解
3、求解
2、代入
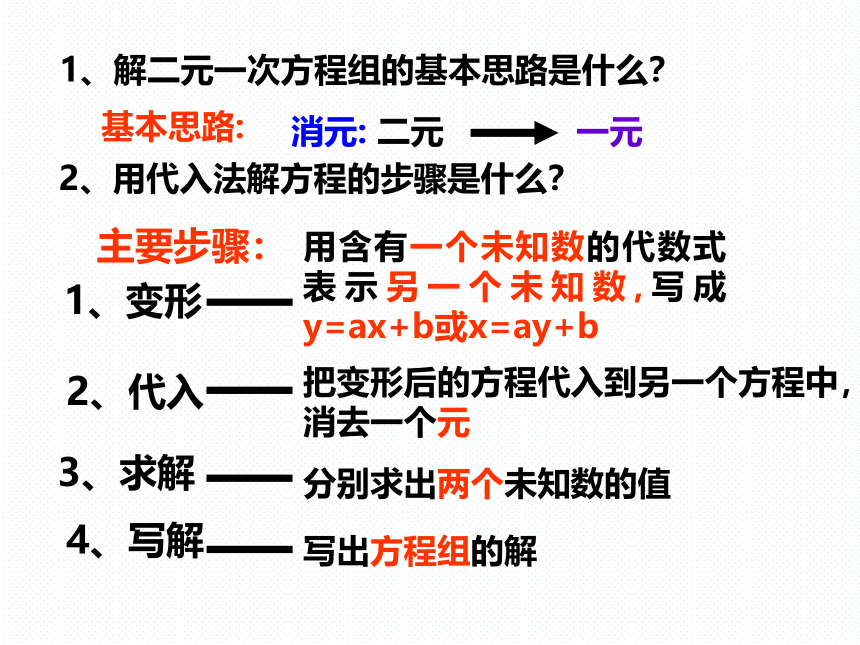
把变形后的方程代入到另一个方程中,消去一个元
分别求出两个未知数的值
写出方程组的解
1、变形
用含有一个未知数的代数式表示另一个未知数,写成y=ax+b或x=ay+b
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
例1:解方程组
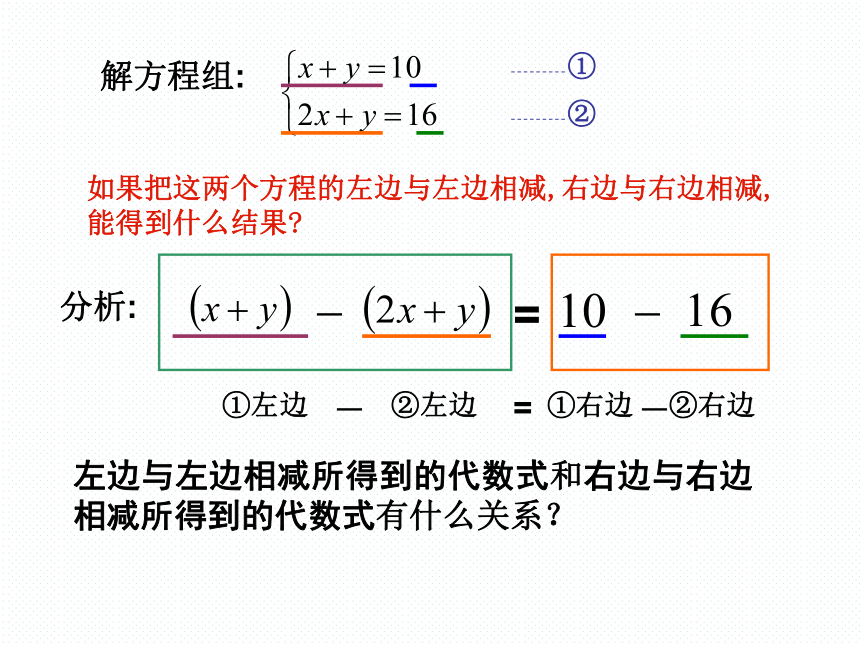
解方程组:
如果把这两个方程的左边与左边相减,右边与右边相减,能得到什么结果?
①
②
分析:
=
①左边
②左边
①右边
②右边
=
左边与左边相减所得到的代数式和右边与右边相减所得到的代数式有什么关系?
解方程组:
②
①
=
分析:
①左边
②左边
①右边
②右边
=
将X=6代入①,得
解方程组:
②
①
解:由①-②得:
将y=-2代入①,得:
即
即
所以方程组的解是
例2:解方程组:
分析:可以发现10y与-10y互为相反数,若把两个方程的左边与左边相加,右边与右边相加,就可以消去未知数y
用什么方法可以消去一个未知数?先消去哪一个比较方便?
解方程组:
解:由①+②得:
将x=0.6代入①,得:
所以方程组的解是
①
②
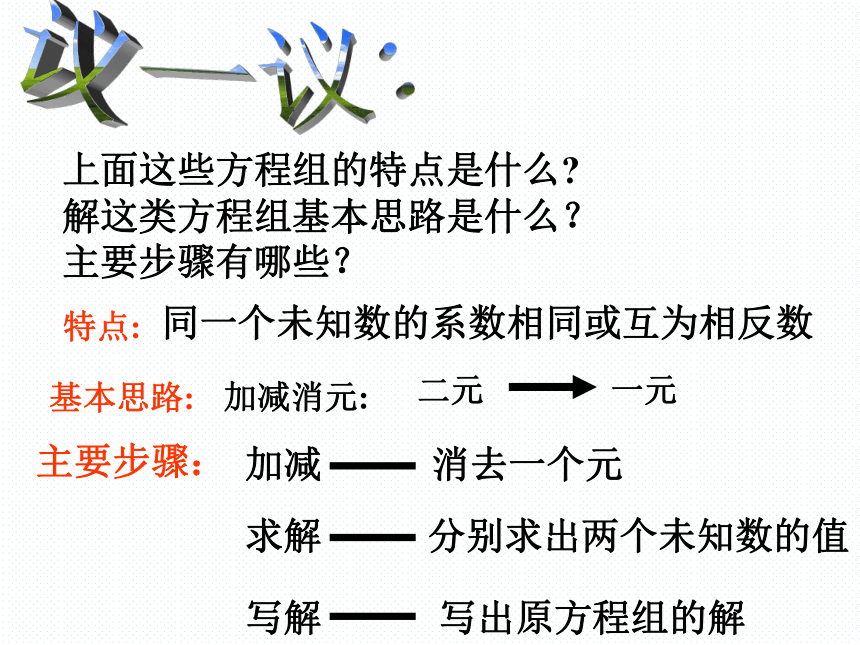
上面这些方程组的特点是什么?
解这类方程组基本思路是什么?
主要步骤有哪些?
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元
加减消元:
消去一个元
分别求出两个未知数的值
写出原方程组的解
同一个未知数的系数相同或互为相反数
总结:当两个二元一次方程中同一个未知数的系数相反或相等时,把两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程。这种方法叫做加减消元法,简称加减法。
同减异加
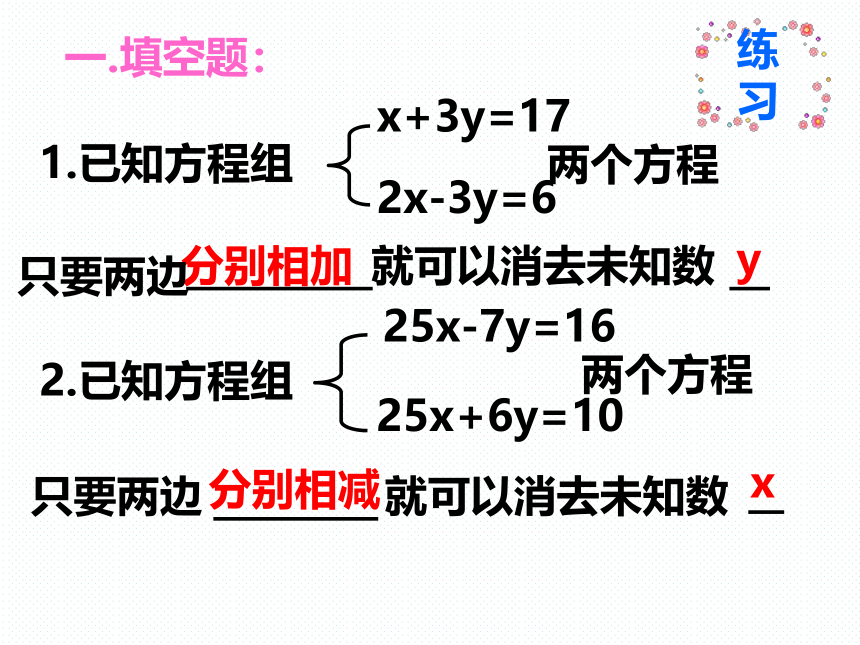
分别相加
y
1.已知方程组
x+3y=17
2x-3y=6
两个方程
就可以消去未知数
分别相减
2.已知方程组
25x-7y=16
25x+6y=10
两个方程
就可以消去未知数
x
一.填空题:
只要两边
只要两边
练习
二:用加减法解二元一次方程组。
⑴
7x-2y=3
9x+2y=-19
⑵
6x-5y=3
6x+y=-15
做一做
x=-1
y=-5
x=-2
y=-3
例3:
问题1.这两个方程直接相加减能消去未知数吗?为什么?
问题2.那么怎样使方程组中某一未知数系数的绝对值相等呢?
例4. 用加减法解方程组:
对于当方程组中两方程不具备上述特点时,必须用等式性质来改变方程组中方程的形式,即得到与原方程组同解的且某未知数系数的绝对值相等的新的方程组,从而为加减消元法解方程组创造条件.
①×3得
所以原方程组的解是
①
②
分析:
③-④得: y=2
把y =2代入①,
解得: x=3
②×2得
6x+9y=36 ③
6x+8y=34 ④
解:
加减法归纳:
用加减法解同一个未知数的系数绝对值不相等,且不成整数倍的二元一次方程组时,把一个(或两个)方程的两边乘以适当的数,使两个方程中某一未知数的系数绝对值相等,从而化为第一类型方程组求解.
1、下列方程组求解过程对吗?若有错误,请给予改正:
解:①一②,得:2x=4-4
x=0
①
②
(1)
解:①一②,得:-2x=12
x=-6
①
②
(2)
解:①×3,得:9x+12y=16 ③
②×2,得:5x-12y=66 ④
③十④,得:14x= 82,
x=41/7
(3)
你能把我们今天内容小结一下吗?
1、 本节课我们知道了用加减消元法解二元一次方程组的基本思路仍是“消元”。主要步骤是:通过两式相加(减)消去其中一个未知数。
2、 把求出的解代入原方程组,可以检验解题过程是否正确。
问题1 本题的等量关系是什么?
2台大收割机2小时的工作量
+5台小收割机2小时的工作量=3.6;
3台大收割机5小时的工作量
+2台小收割机5小时的工作量=8.
例5 2台大收割机和5台小收割机同时工作2 h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5 h收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
解:设1台大收割机和1台小收割机每小时分别收割小麦x hm2 和y hm2 .
依题意得:
问题2 如何设未知数?列出怎样的方程组?
例5 2台大收割机和5台小收割机同时工作2 h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5 h收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
问题3 如何解这个方程组?
例5 2台大收割机和5台小收割机同时工作2 h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5 h收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
解:化简得:
②
①
② - ①,消y 得
解得
代入①,解y
是原方程组的解.
问题5 你能结合教科书上的框图,简述加减消元法解方程组的一般步骤吗?
1,先观察同一未知数的系数关系,能直接加减的直接加减;
2,不能直接加减的,利用等式性质把同一未知数的系数化成相同或相反;
3,两个方程相加或相减消去其中一个未知数;
4,把求出的未知数的值代入较简单的方程求出另一个未知数的值。
灵活运用
问题6 怎样解下面的方程组?
追问1 第一个方程组选择哪种方法更简便?第二个方程组选择哪种方法更简便?
追问2 我们依据什么来选择更简便的方法?
灵活运用
解:选择代入法,由①得,
②
①
代入②,消去y,解得
代入③,得
③
是原方程组的解.
灵活运用
解:选择加减法,
①+②得
②
①
代入①,得
是原方程组的解.
练习
①
②
③
代入法
加减法
解:由①得
将③代入②,得
代入③,得
解:①×4-② ,得
代入①,得
归纳总结
回顾本节课的学习过程,回答以下问题:
(1)结合例题,谈一谈列方程组解决实际问题时应注意什么?
(2)代入消元法和加减消元法有什么联系与区别?如何选择方法运算更简便?
1,两个方程中,遇到有未知数的系数为1的,选用代入法对这个方程进行变形较简便;
2,两个方程中遇到有同一个未知数的系数相同或互为相反数的,选用加减法先消去这个未知数较简便。
1、用代入法解方程的关键是什么?
2、解二元一次方程组的基本思路是什么?
回顾
一元
消元
转化
二元
消元:
二元
一元
主要步骤:
基本思路:
4、写解
3、求解
2、代入
把变形后的方程代入到另一个方程中,消去一个元
分别求出两个未知数的值
写出方程组的解
1、变形
用含有一个未知数的代数式表示另一个未知数,写成y=ax+b或x=ay+b
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
例1:解方程组
解方程组:
如果把这两个方程的左边与左边相减,右边与右边相减,能得到什么结果?
①
②
分析:
=
①左边
②左边
①右边
②右边
=
左边与左边相减所得到的代数式和右边与右边相减所得到的代数式有什么关系?
解方程组:
②
①
=
分析:
①左边
②左边
①右边
②右边
=
将X=6代入①,得
解方程组:
②
①
解:由①-②得:
将y=-2代入①,得:
即
即
所以方程组的解是
例2:解方程组:
分析:可以发现10y与-10y互为相反数,若把两个方程的左边与左边相加,右边与右边相加,就可以消去未知数y
用什么方法可以消去一个未知数?先消去哪一个比较方便?
解方程组:
解:由①+②得:
将x=0.6代入①,得:
所以方程组的解是
①
②
上面这些方程组的特点是什么?
解这类方程组基本思路是什么?
主要步骤有哪些?
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元
加减消元:
消去一个元
分别求出两个未知数的值
写出原方程组的解
同一个未知数的系数相同或互为相反数
总结:当两个二元一次方程中同一个未知数的系数相反或相等时,把两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程。这种方法叫做加减消元法,简称加减法。
同减异加
分别相加
y
1.已知方程组
x+3y=17
2x-3y=6
两个方程
就可以消去未知数
分别相减
2.已知方程组
25x-7y=16
25x+6y=10
两个方程
就可以消去未知数
x
一.填空题:
只要两边
只要两边
练习
二:用加减法解二元一次方程组。
⑴
7x-2y=3
9x+2y=-19
⑵
6x-5y=3
6x+y=-15
做一做
x=-1
y=-5
x=-2
y=-3
例3:
问题1.这两个方程直接相加减能消去未知数吗?为什么?
问题2.那么怎样使方程组中某一未知数系数的绝对值相等呢?
例4. 用加减法解方程组:
对于当方程组中两方程不具备上述特点时,必须用等式性质来改变方程组中方程的形式,即得到与原方程组同解的且某未知数系数的绝对值相等的新的方程组,从而为加减消元法解方程组创造条件.
①×3得
所以原方程组的解是
①
②
分析:
③-④得: y=2
把y =2代入①,
解得: x=3
②×2得
6x+9y=36 ③
6x+8y=34 ④
解:
加减法归纳:
用加减法解同一个未知数的系数绝对值不相等,且不成整数倍的二元一次方程组时,把一个(或两个)方程的两边乘以适当的数,使两个方程中某一未知数的系数绝对值相等,从而化为第一类型方程组求解.
1、下列方程组求解过程对吗?若有错误,请给予改正:
解:①一②,得:2x=4-4
x=0
①
②
(1)
解:①一②,得:-2x=12
x=-6
①
②
(2)
解:①×3,得:9x+12y=16 ③
②×2,得:5x-12y=66 ④
③十④,得:14x= 82,
x=41/7
(3)
你能把我们今天内容小结一下吗?
1、 本节课我们知道了用加减消元法解二元一次方程组的基本思路仍是“消元”。主要步骤是:通过两式相加(减)消去其中一个未知数。
2、 把求出的解代入原方程组,可以检验解题过程是否正确。
问题1 本题的等量关系是什么?
2台大收割机2小时的工作量
+5台小收割机2小时的工作量=3.6;
3台大收割机5小时的工作量
+2台小收割机5小时的工作量=8.
例5 2台大收割机和5台小收割机同时工作2 h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5 h收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
解:设1台大收割机和1台小收割机每小时分别收割小麦x hm2 和y hm2 .
依题意得:
问题2 如何设未知数?列出怎样的方程组?
例5 2台大收割机和5台小收割机同时工作2 h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5 h收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
问题3 如何解这个方程组?
例5 2台大收割机和5台小收割机同时工作2 h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5 h收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
解:化简得:
②
①
② - ①,消y 得
解得
代入①,解y
是原方程组的解.
问题5 你能结合教科书上的框图,简述加减消元法解方程组的一般步骤吗?
1,先观察同一未知数的系数关系,能直接加减的直接加减;
2,不能直接加减的,利用等式性质把同一未知数的系数化成相同或相反;
3,两个方程相加或相减消去其中一个未知数;
4,把求出的未知数的值代入较简单的方程求出另一个未知数的值。
灵活运用
问题6 怎样解下面的方程组?
追问1 第一个方程组选择哪种方法更简便?第二个方程组选择哪种方法更简便?
追问2 我们依据什么来选择更简便的方法?
灵活运用
解:选择代入法,由①得,
②
①
代入②,消去y,解得
代入③,得
③
是原方程组的解.
灵活运用
解:选择加减法,
①+②得
②
①
代入①,得
是原方程组的解.
练习
①
②
③
代入法
加减法
解:由①得
将③代入②,得
代入③,得
解:①×4-② ,得
代入①,得
归纳总结
回顾本节课的学习过程,回答以下问题:
(1)结合例题,谈一谈列方程组解决实际问题时应注意什么?
(2)代入消元法和加减消元法有什么联系与区别?如何选择方法运算更简便?
1,两个方程中,遇到有未知数的系数为1的,选用代入法对这个方程进行变形较简便;
2,两个方程中遇到有同一个未知数的系数相同或互为相反数的,选用加减法先消去这个未知数较简便。
