切线长定理

(共13张PPT)
切
线
长
定
理
三
角
形
内
切
圆
与
切
线
长
定
理
三
角
形
内
切
圆
与
一.自学目标
1.理解切线长、三角形的内切圆与三角形的内心等概念.
2.掌握切线长定理，并能解决与切线长定理有关的证明和计算问题.
二.自学指导
1.回顾旧知
切线的性质：
角平线判定定理：
2.自学P96---P98
3.了解切线长、三角形的内切圆和三角形的内心等概念.
切线长：
三角形的内切圆：
三角形的内心:
4.理解切线长定理，并熟练掌握它的应用.
切线长定理：
圆的切线垂直于过切点的半径.
经过圆外一点作圆的切线，这点和切点之间的线段的长，
叫做这点到圆的切线长.
与三角形各边都相切的圆叫做三角形的内切圆.
三角形三条角平分线的交点，叫做三角形的内心.
从圆外一点可以引圆的两条切线，它们的切线长
相等，这一点和圆心的连线平分两条切线的夹角.
角的内部到角的两边距离相等的点在角的平分线上.
三.自学检测
1.判断：（1）过一点可以作圆的两条切线.（ ）
（2）切线长就是切线的长.（ ）
2.如图，△DEF是⊙I的 三角形，
⊙I是△DEF的 圆，
点I是 △DEF的 心，
它是三角形 的交点.
3. PA、PB分别与⊙O切于点A、B，则
(1) = , ∠ = ∠ .
（2）若连接AB，与OP相交于点M，与⊙O相交于点N,你可以得到哪些结 论？（至少写3个）
×
×
I
D
E
F
．
外切
内切
内
三个角平分线
A
P
O
B
M
N
PA PB
APO BPO
⌒
AB
解：①OP垂直平分AB ② OP平分∠AOB ③图中所有的全等三角形有△AOP≌ △BOP， △AOM≌ △BOM， △AMP≌ △BMP ④图中所有的等腰三角形有△PAB,△OAB ⑤ OP平分 等.
A
P
O
B
M
N
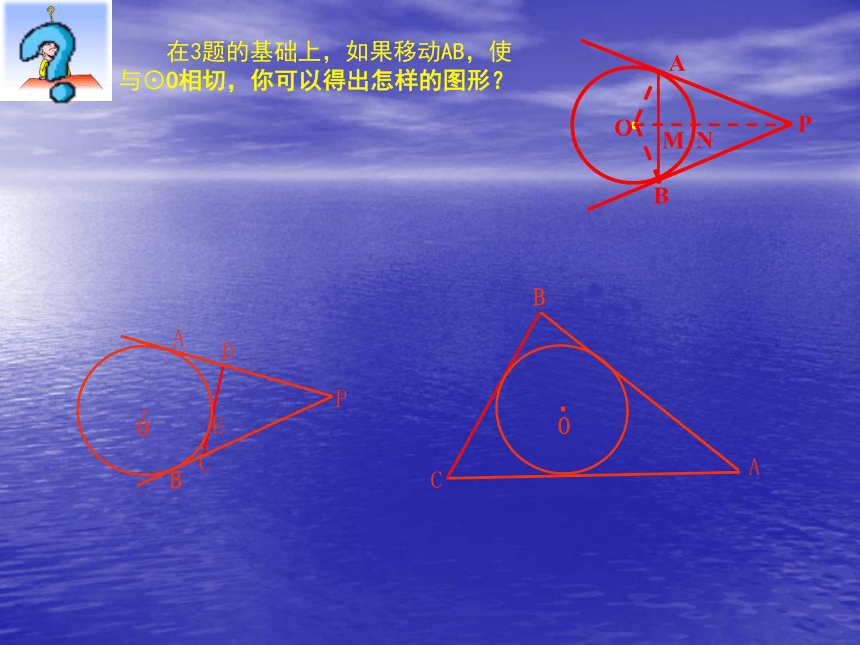
在3题的基础上，如果移动AB，使
与⊙O相切，你可以得出怎样的图形？
D
E
C
A
B
O
.
P
B
C
O
A
.
变式1.如图，PA、PB分别切⊙ O于A、B，CD与⊙O切于点E，分别交
PA，PB于D、C，
（1）若PA=7cm,求△PCD的周长.
（2）若连接OD 、OC且∠P=40°时，求∠DOC的度数。
（1）解：∵PA、DC为⊙O的切线
∴DA=DE （切线长定理）
同理可证 CE=CB，PA=PB
∵し△PCD=PD+PC+CD
=PD+PC+DE+CE
=PD+PC+DA+CB
=PA+PB
=14（cm）
P
A
O
E
D
四.知识拓展
B
C
（2）分析： ∠DOC=（360°- 90°- 90°- 40°）÷ 2 = 70°
变式2. △ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F，
(1)若AB=14cm,BC=13cm，CA=9cm，求AF、BD、CE的长.
（2）若∠C=90°，△ABC 的各边长分别为a、b、c，试猜想内切
圆的半径r与a、b、c的关系，并证明你的猜想.
D
O
F
B
E
C
A
（1）解：设AF=x(cm)，则
AD=x(cm)
CF=CE=9 – x,
BD=BE=14 – x,
由BE + CE=BC可得
（9 – x）+ （14 – x）=13
解得x=5
因此AF=5（cm） BD=9(cm) CE=4(cm).
(2 ) r =
c
a
b
r
分析：a – r + b – r = c
a + b – c =2r
r=
.
.
O
C
A
B
把一个乒乓球放在一个V形架中，如图是它的平面示意图，
CA、CB是⊙O的切线，切点分别是A、B，某同学通过测量，
量得BC=2 cm，∠ACB=600，你能求出乒乓球的半径吗？
解决问题
解：连接OB 、OC
∵ CB是⊙O的切线，∠ACB=60°
∴ ∠BCO=30° ∠OBC=90°
设OB=r(cm) ,则OC=2r(cm)
∵ OB2 +BC2 = OC2
∴r2 + (2 )2=(2r)2
解得 r =2（cm）
通过本节课的学习，你能谈谈自己的收获吗？说一说，让大家一起来分享。
课堂检测
1.必做题：直角三角形的两直角边分别是 6cm，8cm 则
其内切圆半径为______.
2.选做题：已知三角形的内切圆的半径为2cm,周长为
6cm,则其三角形面积为______.
3.提高题：已知圆外切四边形ABCD中(四边分别与圆相切的
四边形称为圆外切四边形)，AB：BC：CD=4：3：2，
它的周长为24cm，则
（1）AB + CD BC + DA(填“＞” 、“＜” 或“＝”)
（2）AB= ，BC= ；
CD= ，DA= .
A
D
O
C
B
8cm
6cm
4cm
6cm
2cm
6cm2
E
F
M
N
A
=
你肯定行！
谢谢大家，再会!