沪科版2020-2021学年度上学期九年级期末数学试卷(含解析)
文档属性
| 名称 | 沪科版2020-2021学年度上学期九年级期末数学试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 156.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 17:41:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2020-2021学年安徽省九年级上学期期末试卷
一、选择题((本大题共10小题,共40.0分))
对于任意实数m,下列函数一定是二次函数的是
A.
B.
C.
D.
在中,,,,则的度数为
A.
B.
C.
D.
对于二次函数的图象,下列说法正确的是
A.
开口向下
B.
对称轴是直线
C.
顶点坐标是
D.
与x轴有两个交点
的值等于
A.
B.
1
C.
D.
关于二次函数,下列说法正确的是
A.
图象与y轴的交点坐标为
B.
y的最小值为
C.
当?时,y的值随x值的大而减小
D.
图象的对称轴在y轴的右侧
如图,∽,则下列比例式正确的是
A.
B.
C.
D.
若,,则a的值为
A.
1
B.
2
C.
4
D.
8
根据下列表格中的对应值,判断a、b、c为常数与x轴的交点的横坐标的取值范围是
x
A.
B.
C.
D.
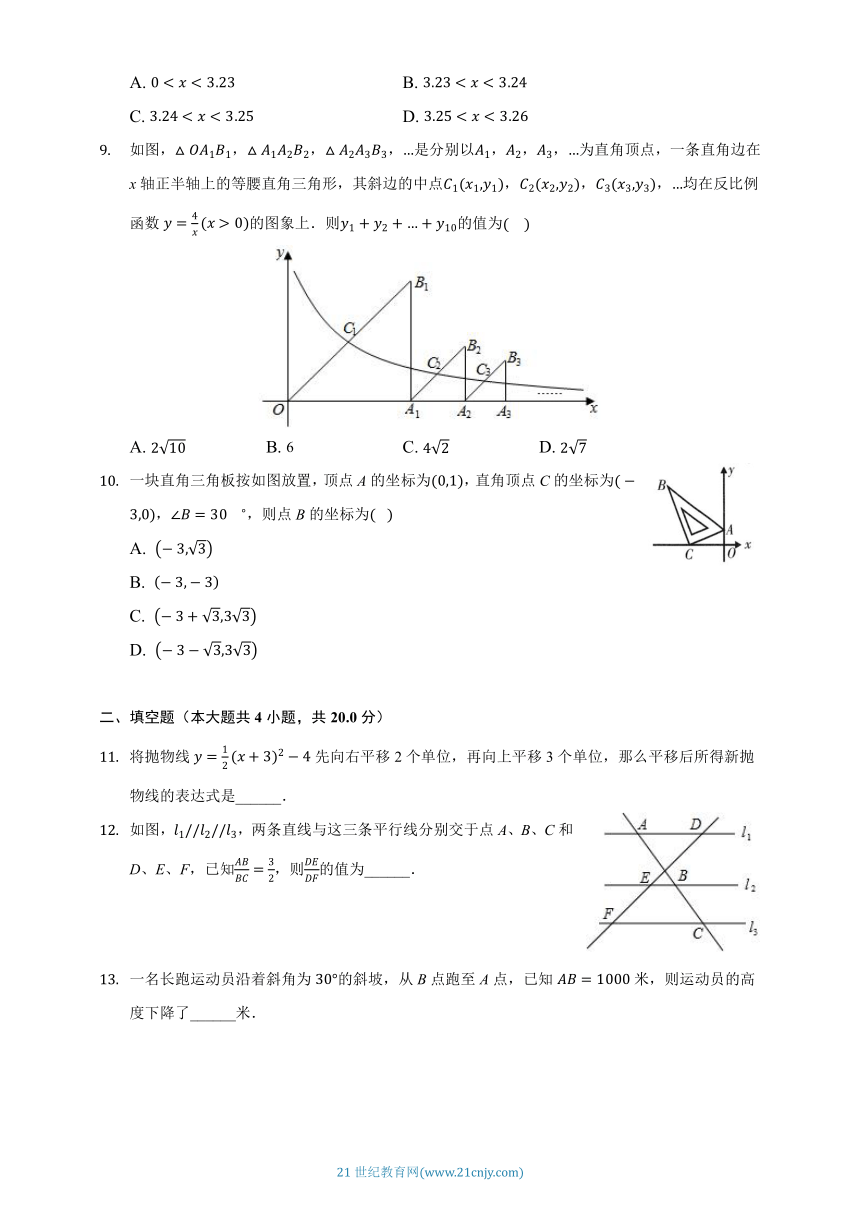
如图,,,,是分别以,,,为直角顶点,一条直角边在x轴正半轴上的等腰直角三角形,其斜边的中点,,,均在反比例函数的图象上.则的值为
A.
B.
6
C.
D.
一块直角三角板按如图放置,顶点A的坐标为,直角顶点C的坐标为,,则点B的坐标为???
A.
B.
C.
D.
二、填空题(本大题共4小题,共20.0分)
将抛物线先向右平移2个单位,再向上平移3个单位,那么平移后所得新抛物线的表达式是______.
如图,,两条直线与这三条平行线分别交于点A、B、C和D、E、F,已知,则的值为______.
一名长跑运动员沿着斜角为的斜坡,从B点跑至A点,已知米,则运动员的高度下降了______米.
如图,二次函数的图象与x轴交于A、B两点点A在点B的左边,与y轴交于点C,其对称轴与x轴交于点D,若P为y轴上的一个动点,连接PD,则的最小值为______.
三、(本大题共2小题,共16.0分)
计算:.
如图,点D、E分别在的边AB、AC上,若,,.
求证:∽;
已知,AD::3,,求AC的长.
四、(本大题共2小题,共16.0分)
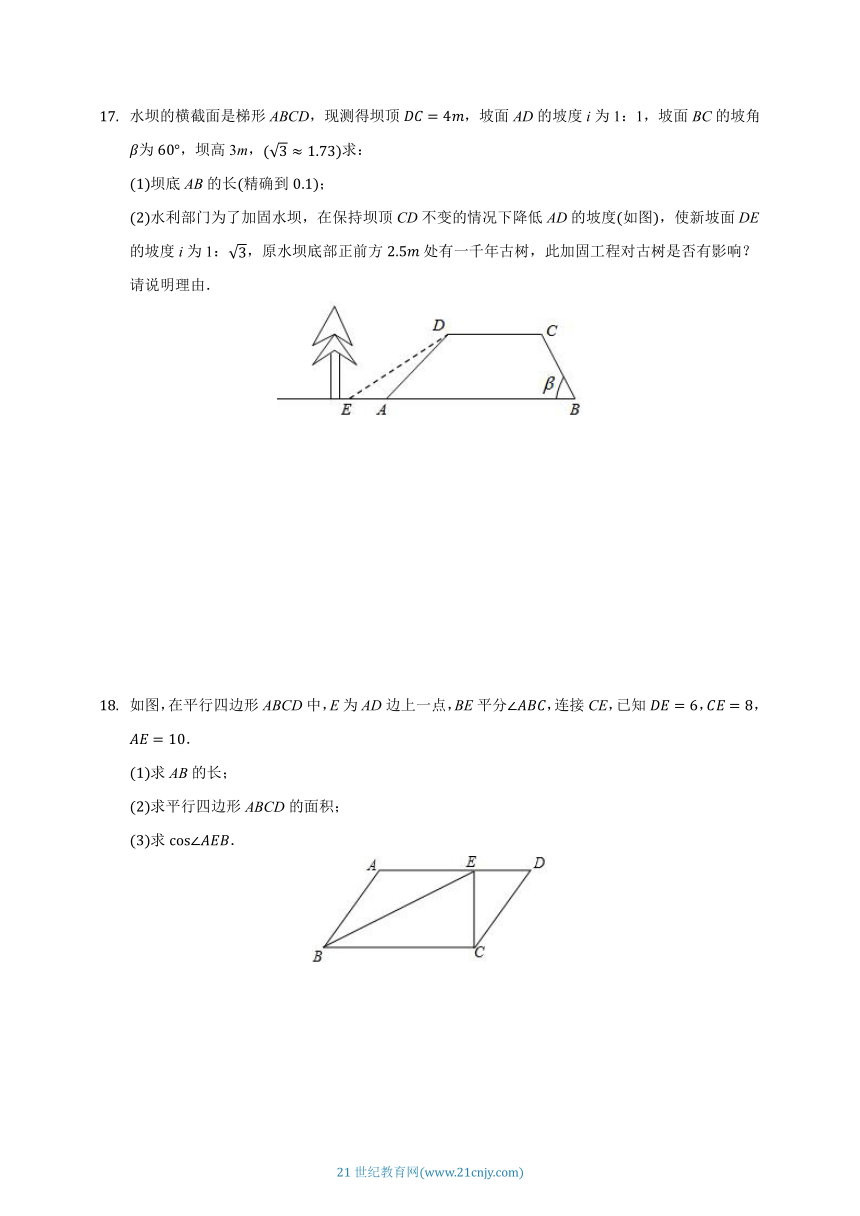
水坝的横截面是梯形ABCD,现测得坝顶,坡面AD的坡度i为1:1,坡面BC的坡角为,坝高3m,求:
坝底AB的长精确到;
水利部门为了加固水坝,在保持坝顶CD不变的情况下降低AD的坡度如图,使新坡面DE的坡度i为1:,原水坝底部正前方处有一千年古树,此加固工程对古树是否有影响?请说明理由.
如图,在平行四边形ABCD中,E为AD边上一点,BE平分,连接CE,已知,,.
求AB的长;
求平行四边形ABCD的面积;
求.
五、(本大题共2小题,共20.0分)
小甬工作的办公楼矩形前有一旗杆MN,,旗杆高为12m,在办公楼底A处测得旗杆顶的仰角为,在办公楼天台B处测旗杆顶的仰角为,在小甬所在办公室楼层E处测得旗杆顶的俯角为.
办公楼的高度AB;
求小甬所在办公室楼层的高度AE.
昆明市某化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量千克是销售单价元千克的一次函数,且当时,;时,在销售过程中,每天还要支付其他费用450元.
求出y与x的函数关系式,并写出自变量x的取值范围.
求该公司销售该原料日获利元与销售单价元千克之间的函数关系式.
当销售单价为多少元千克时,该公司日获利最大?最大获利是多少元?
六、(本题满分12.0分)
如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,于点G,于点F,.
求证:∽;
若,,求的值.
六、(本题满分12.0分)
如图,抛物线与x轴交于A,B两点在B的左侧,与y轴交于点,点D与C关于抛物线的对称轴对称.
求抛物线的解析式及点D的坐标;
点P是抛物线上的一点,当的面积是8,求出点P的坐标;
过直线AD下方的抛物线上一点M作y轴的平行线,与直线AD交于点N,已知M点的横坐标是m,试用含m的式子表示MN的长及的面积S,并求当MN的长最大时S的值.
六、(本题满分14.0分)
如图,已知边长为10的正方形ABCD,E是BC边上一动点与B、C不重合,连结AE,G是BC延长线上的点,过点E作AE的垂线交的角平分线于点F,若.
求证:∽;
若,求的面积;
请直接写出EC为何值时,的面积最大.
答案和解析
1.【答案】B
【解析】
【分析】
本题主要考查了二次函数的定义,是一个基础题目.根据二次函数的定义:二次项系数不为0,举出特例即可判断.
【解答】
解:当时,二次项系数等于0,不是二次函数,故错误;
B.是二次函数,故正确;
C.当时,二次项系数等于0,不是二次函数,故错误;
D.当或时,二次项系数等于0,不是二次函数,故错误.
故选B.
2.【答案】C
【解析】解:在中,,,
,
则.
故选:C.
首先作出图形,可得,继而可求得的度数.
本题考查了解直角三角形,解答本题的关键是根据题意做出图形,利用特殊角的三角函数值求解.
3.【答案】C
【解析】解:二次函数的图象的开口向上,对称轴为直线,顶点坐标为,
当时,,此方程没有实数解,所以抛物线与x轴没有交点.
故选:C.
利用二次函数的性质对A、B、C进行判断;利用的实数解的个数对D进行判断.
本题考查了抛物线与x轴的交点:把求二次函数b,c是常数,与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.
4.【答案】B
【解析】解:.
故选:B.
直接利用特殊角的三角函数值代入得出答案.
此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.
5.【答案】B
【解析】解:,
当时,,故选项A错误,
当时,y取得最小值,此时,故选项B正确,
当时,y随x的增大而减小,故选项C错误,
该函数的对称轴是直线,故选项D错误,
故选:B.
根据题目中的函数解析式可以判断各个选项中的结论是否成立,从而可以解答本题.
本题考查二次函数的性质、二次函数的最值,解答本题的关键是明确题意,利用二次函数的性质解答.
6.【答案】D
【解析】
【分析】
此题考查了相似三角形的性质.此题比较简单,注意掌握相似三角形的对应边成比例定理的应用是解此题的关键.
由∽,根据相似三角形的对应边成比例,即可求得答案.
【解答】
解:∽,
.
故选:D.
7.【答案】C
【解析】解:设,
则,,,
,
,
解得:,
即,
故选:C.
设,根据比例的性质得出,,,代入,再求出k即可.
本题考查了比例的性质,能熟记比例的性质的内容是解此题的关键,注意:如果,那么.
8.【答案】C
【解析】解:时,;时,,
抛物线与x轴的一个交点在点与点之间.
故选:C.
利用和对应的函数值一负一正,从而可判断函数值为对应的自变量的范围.
本题考查了抛物线与x轴的交点:把求二次函数b,c是常数,与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.
9.【答案】A
【解析】解:过、、分别作x轴的垂线,垂足分别为、、
其斜边的中点在反比例函数,即,
,
设,则此时,代入得:,
解得:,即:,
同理:,
,
,
故选:A.
根据点的坐标,确定,可求反比例函数关系式,由点是等腰直角三角形的斜边中点,可以得到的长,然后再设未知数,表示点的坐标,确定,代入反比例函数的关系式,建立方程解出未知数,表示点的坐标,确定,然后再求和.
考查反比例函数的图象和性质、反比例函数图象上点的坐标特征、等腰直角三角形的性质等知识,通过计算有一定的规律,推断出一般性的结论,得出答案.
10.【答案】D
【解析】
【分析】
本题考查了全等三角形的判定与性质以及坐标与图形的性质,解答本题的关键是作出合适的辅助线,证明三角形的相似,进而求解.过点B作于点D,根据为直角三角形可证明∽,设点B坐标为,根据相似三角形的性质即可求解.
【解答】
解:过点B作于点D,
为直角三角形,
,
∽,
,
设点B坐标为,
则,
,
,
,
,
,
解得:,
则.
即点B的坐标为
故选:D.
11.【答案】
【解析】【试题解析】
解:将抛物线向右平移2个单位所得直线解析式为:;
再向上平移3个单位为:,即.
故答案是:.
根据“左加右减、上加下减”的原则进行解答即可.
此题主要考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.
12.【答案】
【解析】
【分析】此题主要考查了平行线分线段成比例定理,得出是解题的关键.
直接利用平行线分线段成比例定理进而得出,再将已知数据代入求出即可.
【解答】解:,
,
,
,
.
故答案为.
13.【答案】500
【解析】
【分析】
本题考查了解直角三角形的应用,解答本题的关键是根据坡角构造直角三角形,利用三角函数的知识求解.根据题意,从B点跑至A点,实际下降的高度为BC,在中,求出BC的长度即可.
【解答】
解:在中,
米,,
米.
故答案为500.
14.【答案】
【解析】【试题解析】
解:连接AC
与x轴交点、,点,对称轴,
,
作点D关于y轴的对称点,作点A关于y轴的对称点,过点作于点E,则为所求;
由对称性可知,,
,
,
再由,
的最小值为,
,,
,,,
,
;
故答案为;
连接AC,作点D关于y轴的对称点,作点A关于y轴的对称点,过点作于点E,则为所求;由对称性可知,,,,,由的余弦值可得,即可求出;
本题考查了抛物线与x轴的交点,二次函数的性质,轴对称最短路径问题,解直角三角形.
15.【答案】解:
.
【解析】本题涉及零指数幂、特殊角的三角函数值、绝对值、二次根式化简4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握零指数幂、特殊角的三角函数值、绝对值、二次根式等考点的运算.
16.【答案】证明:在中,,,,
,
又在中,,,
,,
∽;
解:∽,
,
,,
,
.
【解析】根据三角形内角和定理以及相似三角形的判定定理即可求出答案.
根据相似三角形的性质即可求出答案.
本题考查了三角形内角和定理及相似三角形的判定与性质,解题的关键是熟练运用相似三角形的性质与判定.
17.【答案】解:如图,分别过C、D作,,垂足分别为F、H,
得四边形CDHF是矩形,
,,
在中,由坡度:1,
得,
在中,,,
得,
则;
则坝底AB的长约为;
由题意得,中,DH::,
,
则,
,
所以没有影响.
【解析】分别过C、D作,,垂足分别为F、H,易得四边形CDHF是矩形,从而,,在中,由坡度:1,易得,在中,坡面BC的坡角为,坝高3m,易得BF,则;
由题意得,中,由坡面DE的坡度i为1:,易得的值进而与比较即可.
本题考查了解直角三角形的应用坡度坡角问题,解决本题的关键是掌握坡度坡角定义.
18.【答案】解:四边形ABCD是平行四边形,
,
,
平分,
,
,
四边形ABCD是平行四边形.
,
在中,,,,
,
.
,
平行四边形ABCD的面积;
四边形ABCD是平行四边形.
,,
,,
中,,
.
【解析】由平行四边形的性质及角平分线的定义可得出,进而再利用题中数据即可求解结论;
易证为直角三角形,则,基础CE为平行四边形的高,利用平行四边形的面积公式计算即可;
易证,求的值可转化为求的值,利用勾股定理求出BE的长即可.
本题主要考查平行四边形的性质、平行四边形的面积公式运用、解直角三角形的有关知识及角平分线的性质等问题,应熟练掌握.
19.【答案】解:如图,过点M作于点H,
,,
四边形MNAH是矩形,
,
,
,
在中,,
,
,
.
答:办公楼的高度AB为.
过点E作于点Q,
由得,,
,
设,则,
,
由,
,
解得.
答:小甬所在办公室楼层的高度AE为.
【解析】过点M作于点H,可得四边形MNAH是矩形,再根据锐角三角函数即可求出办公楼的高度AB;
过点E作于点Q,设,则,,由,列出方程即可求出小甬所在办公室楼层的高度AE.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
20.【答案】解:设,根据题意得,
解得:,,
;
;
,
,
时,w有最大值为1950元,
当销售单价为60元时,该公司日获利最大,为1950元.
【解析】根据y与x成一次函数解析式,设为,把x与y的两对值代入求出k与b的值,即可确定出y与x的解析式,并求出x的范围即可;
根据利润单价销售量列出W关于x的二次函数解析式即可;
利用二次函数的性质求出W的最大值,以及此时x的值即可.
此题考查了二次函数的应用,待定系数法求一次函数解析式,以及二次函数的性质,熟练掌握二次函数性质是解本题的关键.
21.【答案】解:,,
,
,
,
,
∽,
由可知:∽,
由可知:,
,
∽,
,
.
【解析】本题考查相似三角形的判定与性质,解题的关键是熟练运用相似三角形的判定,本题属于中等题型.
由于,,所以,从而可证明,进而可证明∽;
由∽,得,又易证∽,所以,从而可知.
22.【答案】解:抛物线与y轴交于点,
,
,
抛物线的解析式为,
抛物线的对称轴为直线.
点D与C关于抛物线的对称轴对称,
点D的坐标为.
当时,,
解得:,,
点A的坐标为,点B的坐标为,.
设点P的坐标为,
的面积是8,
,即,
.
当时,,解得:,,
点P的坐标为或;
当时,,解得:,
点P的坐标为.
当的面积是8,点P的坐标为或或.
设直线AD的解析式为,
将,代入,得:,
解得:,
直线AD的解析式为.
点M的横坐标是,
点M的坐标为,点N的坐标为,
,.
,,
当时,MN取得最大值,最大值为,此时S的值为,
当MN的长最大时S的值为.
【解析】根据点C的坐标,利用二次函数图象上点的坐标特征可求出n值,进而可得出抛物线的解析式,由抛物线的解析式利用二次函数的性质可得出抛物线的对称轴,结合点C的坐标可得出点D的坐标;
利用二次函数图象上点的坐标特征可求出点A,B的坐标及AB的长,设点P的坐标为,由三角形的面积公式结合的面积是8,可求出b值,再利用二次函数图象上点的坐标特征可求出点P的坐标;
根据点A,D的坐标利用待定系数法可求出直线AD的解析式,由点M的横坐标为m可得出点M,N的坐标,进而可得出MN的长,结合可用含m的式子表示的面积S,再利用二次函数的性质即可解决最值问题.
本题考查了二次函数图象上点的坐标特征、二次函数的性质、三角形的面积、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,解题的关键是:根据点的坐标,利用二次函数图象上点的坐标特征求出n值;利用三角形的面积公式,求出点P的纵坐标;利用二次函数的性质,求出MN的最大值.
23.【答案】解:四边形ABCD是正方形,
,
平分,
,
,
,
,
四边形ABCD是正方形,,
,
,,
,
,
∽;
,,
,
,
,
由知,∽,
,
,
,
;
设,则,
,
由知,∽,
,
,
,
,
当时,.
【解析】先判断出,再利用同角的余角相等,判断出,进而得出∽,即可得出结论;
先求出,进而表示出,由∽,得出,求出FG,最后用三角形面积公式即可得出结论;
同的方法,即可得出,即可得出结论.
此题是相似形综合题,主要考查了正方形的性质,角平分线,相似三角形的判定和性质,三角形的面积公式,判断出∽是解本题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
2020-2021学年安徽省九年级上学期期末试卷
一、选择题((本大题共10小题,共40.0分))
对于任意实数m,下列函数一定是二次函数的是
A.
B.
C.
D.
在中,,,,则的度数为
A.
B.
C.
D.
对于二次函数的图象,下列说法正确的是
A.
开口向下
B.
对称轴是直线
C.
顶点坐标是
D.
与x轴有两个交点
的值等于
A.
B.
1
C.
D.
关于二次函数,下列说法正确的是
A.
图象与y轴的交点坐标为
B.
y的最小值为
C.
当?时,y的值随x值的大而减小
D.
图象的对称轴在y轴的右侧
如图,∽,则下列比例式正确的是
A.
B.
C.
D.
若,,则a的值为
A.
1
B.
2
C.
4
D.
8
根据下列表格中的对应值,判断a、b、c为常数与x轴的交点的横坐标的取值范围是
x
A.
B.
C.
D.
如图,,,,是分别以,,,为直角顶点,一条直角边在x轴正半轴上的等腰直角三角形,其斜边的中点,,,均在反比例函数的图象上.则的值为
A.
B.
6
C.
D.
一块直角三角板按如图放置,顶点A的坐标为,直角顶点C的坐标为,,则点B的坐标为???
A.
B.
C.
D.
二、填空题(本大题共4小题,共20.0分)
将抛物线先向右平移2个单位,再向上平移3个单位,那么平移后所得新抛物线的表达式是______.
如图,,两条直线与这三条平行线分别交于点A、B、C和D、E、F,已知,则的值为______.
一名长跑运动员沿着斜角为的斜坡,从B点跑至A点,已知米,则运动员的高度下降了______米.
如图,二次函数的图象与x轴交于A、B两点点A在点B的左边,与y轴交于点C,其对称轴与x轴交于点D,若P为y轴上的一个动点,连接PD,则的最小值为______.
三、(本大题共2小题,共16.0分)
计算:.
如图,点D、E分别在的边AB、AC上,若,,.
求证:∽;
已知,AD::3,,求AC的长.
四、(本大题共2小题,共16.0分)
水坝的横截面是梯形ABCD,现测得坝顶,坡面AD的坡度i为1:1,坡面BC的坡角为,坝高3m,求:
坝底AB的长精确到;
水利部门为了加固水坝,在保持坝顶CD不变的情况下降低AD的坡度如图,使新坡面DE的坡度i为1:,原水坝底部正前方处有一千年古树,此加固工程对古树是否有影响?请说明理由.
如图,在平行四边形ABCD中,E为AD边上一点,BE平分,连接CE,已知,,.
求AB的长;
求平行四边形ABCD的面积;
求.
五、(本大题共2小题,共20.0分)
小甬工作的办公楼矩形前有一旗杆MN,,旗杆高为12m,在办公楼底A处测得旗杆顶的仰角为,在办公楼天台B处测旗杆顶的仰角为,在小甬所在办公室楼层E处测得旗杆顶的俯角为.
办公楼的高度AB;
求小甬所在办公室楼层的高度AE.
昆明市某化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量千克是销售单价元千克的一次函数,且当时,;时,在销售过程中,每天还要支付其他费用450元.
求出y与x的函数关系式,并写出自变量x的取值范围.
求该公司销售该原料日获利元与销售单价元千克之间的函数关系式.
当销售单价为多少元千克时,该公司日获利最大?最大获利是多少元?
六、(本题满分12.0分)
如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,于点G,于点F,.
求证:∽;
若,,求的值.
六、(本题满分12.0分)
如图,抛物线与x轴交于A,B两点在B的左侧,与y轴交于点,点D与C关于抛物线的对称轴对称.
求抛物线的解析式及点D的坐标;
点P是抛物线上的一点,当的面积是8,求出点P的坐标;
过直线AD下方的抛物线上一点M作y轴的平行线,与直线AD交于点N,已知M点的横坐标是m,试用含m的式子表示MN的长及的面积S,并求当MN的长最大时S的值.
六、(本题满分14.0分)
如图,已知边长为10的正方形ABCD,E是BC边上一动点与B、C不重合,连结AE,G是BC延长线上的点,过点E作AE的垂线交的角平分线于点F,若.
求证:∽;
若,求的面积;
请直接写出EC为何值时,的面积最大.
答案和解析
1.【答案】B
【解析】
【分析】
本题主要考查了二次函数的定义,是一个基础题目.根据二次函数的定义:二次项系数不为0,举出特例即可判断.
【解答】
解:当时,二次项系数等于0,不是二次函数,故错误;
B.是二次函数,故正确;
C.当时,二次项系数等于0,不是二次函数,故错误;
D.当或时,二次项系数等于0,不是二次函数,故错误.
故选B.
2.【答案】C
【解析】解:在中,,,
,
则.
故选:C.
首先作出图形,可得,继而可求得的度数.
本题考查了解直角三角形,解答本题的关键是根据题意做出图形,利用特殊角的三角函数值求解.
3.【答案】C
【解析】解:二次函数的图象的开口向上,对称轴为直线,顶点坐标为,
当时,,此方程没有实数解,所以抛物线与x轴没有交点.
故选:C.
利用二次函数的性质对A、B、C进行判断;利用的实数解的个数对D进行判断.
本题考查了抛物线与x轴的交点:把求二次函数b,c是常数,与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.
4.【答案】B
【解析】解:.
故选:B.
直接利用特殊角的三角函数值代入得出答案.
此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.
5.【答案】B
【解析】解:,
当时,,故选项A错误,
当时,y取得最小值,此时,故选项B正确,
当时,y随x的增大而减小,故选项C错误,
该函数的对称轴是直线,故选项D错误,
故选:B.
根据题目中的函数解析式可以判断各个选项中的结论是否成立,从而可以解答本题.
本题考查二次函数的性质、二次函数的最值,解答本题的关键是明确题意,利用二次函数的性质解答.
6.【答案】D
【解析】
【分析】
此题考查了相似三角形的性质.此题比较简单,注意掌握相似三角形的对应边成比例定理的应用是解此题的关键.
由∽,根据相似三角形的对应边成比例,即可求得答案.
【解答】
解:∽,
.
故选:D.
7.【答案】C
【解析】解:设,
则,,,
,
,
解得:,
即,
故选:C.
设,根据比例的性质得出,,,代入,再求出k即可.
本题考查了比例的性质,能熟记比例的性质的内容是解此题的关键,注意:如果,那么.
8.【答案】C
【解析】解:时,;时,,
抛物线与x轴的一个交点在点与点之间.
故选:C.
利用和对应的函数值一负一正,从而可判断函数值为对应的自变量的范围.
本题考查了抛物线与x轴的交点:把求二次函数b,c是常数,与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.
9.【答案】A
【解析】解:过、、分别作x轴的垂线,垂足分别为、、
其斜边的中点在反比例函数,即,
,
设,则此时,代入得:,
解得:,即:,
同理:,
,
,
故选:A.
根据点的坐标,确定,可求反比例函数关系式,由点是等腰直角三角形的斜边中点,可以得到的长,然后再设未知数,表示点的坐标,确定,代入反比例函数的关系式,建立方程解出未知数,表示点的坐标,确定,然后再求和.
考查反比例函数的图象和性质、反比例函数图象上点的坐标特征、等腰直角三角形的性质等知识,通过计算有一定的规律,推断出一般性的结论,得出答案.
10.【答案】D
【解析】
【分析】
本题考查了全等三角形的判定与性质以及坐标与图形的性质,解答本题的关键是作出合适的辅助线,证明三角形的相似,进而求解.过点B作于点D,根据为直角三角形可证明∽,设点B坐标为,根据相似三角形的性质即可求解.
【解答】
解:过点B作于点D,
为直角三角形,
,
∽,
,
设点B坐标为,
则,
,
,
,
,
,
解得:,
则.
即点B的坐标为
故选:D.
11.【答案】
【解析】【试题解析】
解:将抛物线向右平移2个单位所得直线解析式为:;
再向上平移3个单位为:,即.
故答案是:.
根据“左加右减、上加下减”的原则进行解答即可.
此题主要考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.
12.【答案】
【解析】
【分析】此题主要考查了平行线分线段成比例定理,得出是解题的关键.
直接利用平行线分线段成比例定理进而得出,再将已知数据代入求出即可.
【解答】解:,
,
,
,
.
故答案为.
13.【答案】500
【解析】
【分析】
本题考查了解直角三角形的应用,解答本题的关键是根据坡角构造直角三角形,利用三角函数的知识求解.根据题意,从B点跑至A点,实际下降的高度为BC,在中,求出BC的长度即可.
【解答】
解:在中,
米,,
米.
故答案为500.
14.【答案】
【解析】【试题解析】
解:连接AC
与x轴交点、,点,对称轴,
,
作点D关于y轴的对称点,作点A关于y轴的对称点,过点作于点E,则为所求;
由对称性可知,,
,
,
再由,
的最小值为,
,,
,,,
,
;
故答案为;
连接AC,作点D关于y轴的对称点,作点A关于y轴的对称点,过点作于点E,则为所求;由对称性可知,,,,,由的余弦值可得,即可求出;
本题考查了抛物线与x轴的交点,二次函数的性质,轴对称最短路径问题,解直角三角形.
15.【答案】解:
.
【解析】本题涉及零指数幂、特殊角的三角函数值、绝对值、二次根式化简4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握零指数幂、特殊角的三角函数值、绝对值、二次根式等考点的运算.
16.【答案】证明:在中,,,,
,
又在中,,,
,,
∽;
解:∽,
,
,,
,
.
【解析】根据三角形内角和定理以及相似三角形的判定定理即可求出答案.
根据相似三角形的性质即可求出答案.
本题考查了三角形内角和定理及相似三角形的判定与性质,解题的关键是熟练运用相似三角形的性质与判定.
17.【答案】解:如图,分别过C、D作,,垂足分别为F、H,
得四边形CDHF是矩形,
,,
在中,由坡度:1,
得,
在中,,,
得,
则;
则坝底AB的长约为;
由题意得,中,DH::,
,
则,
,
所以没有影响.
【解析】分别过C、D作,,垂足分别为F、H,易得四边形CDHF是矩形,从而,,在中,由坡度:1,易得,在中,坡面BC的坡角为,坝高3m,易得BF,则;
由题意得,中,由坡面DE的坡度i为1:,易得的值进而与比较即可.
本题考查了解直角三角形的应用坡度坡角问题,解决本题的关键是掌握坡度坡角定义.
18.【答案】解:四边形ABCD是平行四边形,
,
,
平分,
,
,
四边形ABCD是平行四边形.
,
在中,,,,
,
.
,
平行四边形ABCD的面积;
四边形ABCD是平行四边形.
,,
,,
中,,
.
【解析】由平行四边形的性质及角平分线的定义可得出,进而再利用题中数据即可求解结论;
易证为直角三角形,则,基础CE为平行四边形的高,利用平行四边形的面积公式计算即可;
易证,求的值可转化为求的值,利用勾股定理求出BE的长即可.
本题主要考查平行四边形的性质、平行四边形的面积公式运用、解直角三角形的有关知识及角平分线的性质等问题,应熟练掌握.
19.【答案】解:如图,过点M作于点H,
,,
四边形MNAH是矩形,
,
,
,
在中,,
,
,
.
答:办公楼的高度AB为.
过点E作于点Q,
由得,,
,
设,则,
,
由,
,
解得.
答:小甬所在办公室楼层的高度AE为.
【解析】过点M作于点H,可得四边形MNAH是矩形,再根据锐角三角函数即可求出办公楼的高度AB;
过点E作于点Q,设,则,,由,列出方程即可求出小甬所在办公室楼层的高度AE.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
20.【答案】解:设,根据题意得,
解得:,,
;
;
,
,
时,w有最大值为1950元,
当销售单价为60元时,该公司日获利最大,为1950元.
【解析】根据y与x成一次函数解析式,设为,把x与y的两对值代入求出k与b的值,即可确定出y与x的解析式,并求出x的范围即可;
根据利润单价销售量列出W关于x的二次函数解析式即可;
利用二次函数的性质求出W的最大值,以及此时x的值即可.
此题考查了二次函数的应用,待定系数法求一次函数解析式,以及二次函数的性质,熟练掌握二次函数性质是解本题的关键.
21.【答案】解:,,
,
,
,
,
∽,
由可知:∽,
由可知:,
,
∽,
,
.
【解析】本题考查相似三角形的判定与性质,解题的关键是熟练运用相似三角形的判定,本题属于中等题型.
由于,,所以,从而可证明,进而可证明∽;
由∽,得,又易证∽,所以,从而可知.
22.【答案】解:抛物线与y轴交于点,
,
,
抛物线的解析式为,
抛物线的对称轴为直线.
点D与C关于抛物线的对称轴对称,
点D的坐标为.
当时,,
解得:,,
点A的坐标为,点B的坐标为,.
设点P的坐标为,
的面积是8,
,即,
.
当时,,解得:,,
点P的坐标为或;
当时,,解得:,
点P的坐标为.
当的面积是8,点P的坐标为或或.
设直线AD的解析式为,
将,代入,得:,
解得:,
直线AD的解析式为.
点M的横坐标是,
点M的坐标为,点N的坐标为,
,.
,,
当时,MN取得最大值,最大值为,此时S的值为,
当MN的长最大时S的值为.
【解析】根据点C的坐标,利用二次函数图象上点的坐标特征可求出n值,进而可得出抛物线的解析式,由抛物线的解析式利用二次函数的性质可得出抛物线的对称轴,结合点C的坐标可得出点D的坐标;
利用二次函数图象上点的坐标特征可求出点A,B的坐标及AB的长,设点P的坐标为,由三角形的面积公式结合的面积是8,可求出b值,再利用二次函数图象上点的坐标特征可求出点P的坐标;
根据点A,D的坐标利用待定系数法可求出直线AD的解析式,由点M的横坐标为m可得出点M,N的坐标,进而可得出MN的长,结合可用含m的式子表示的面积S,再利用二次函数的性质即可解决最值问题.
本题考查了二次函数图象上点的坐标特征、二次函数的性质、三角形的面积、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,解题的关键是:根据点的坐标,利用二次函数图象上点的坐标特征求出n值;利用三角形的面积公式,求出点P的纵坐标;利用二次函数的性质,求出MN的最大值.
23.【答案】解:四边形ABCD是正方形,
,
平分,
,
,
,
,
四边形ABCD是正方形,,
,
,,
,
,
∽;
,,
,
,
,
由知,∽,
,
,
,
;
设,则,
,
由知,∽,
,
,
,
,
当时,.
【解析】先判断出,再利用同角的余角相等,判断出,进而得出∽,即可得出结论;
先求出,进而表示出,由∽,得出,求出FG,最后用三角形面积公式即可得出结论;
同的方法,即可得出,即可得出结论.
此题是相似形综合题,主要考查了正方形的性质,角平分线,相似三角形的判定和性质,三角形的面积公式,判断出∽是解本题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
