人教版八年级上册第十一章 三角形知识点复习及习题练习(无答案)
文档属性
| 名称 | 人教版八年级上册第十一章 三角形知识点复习及习题练习(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 22:07:16 | ||
图片预览



文档简介
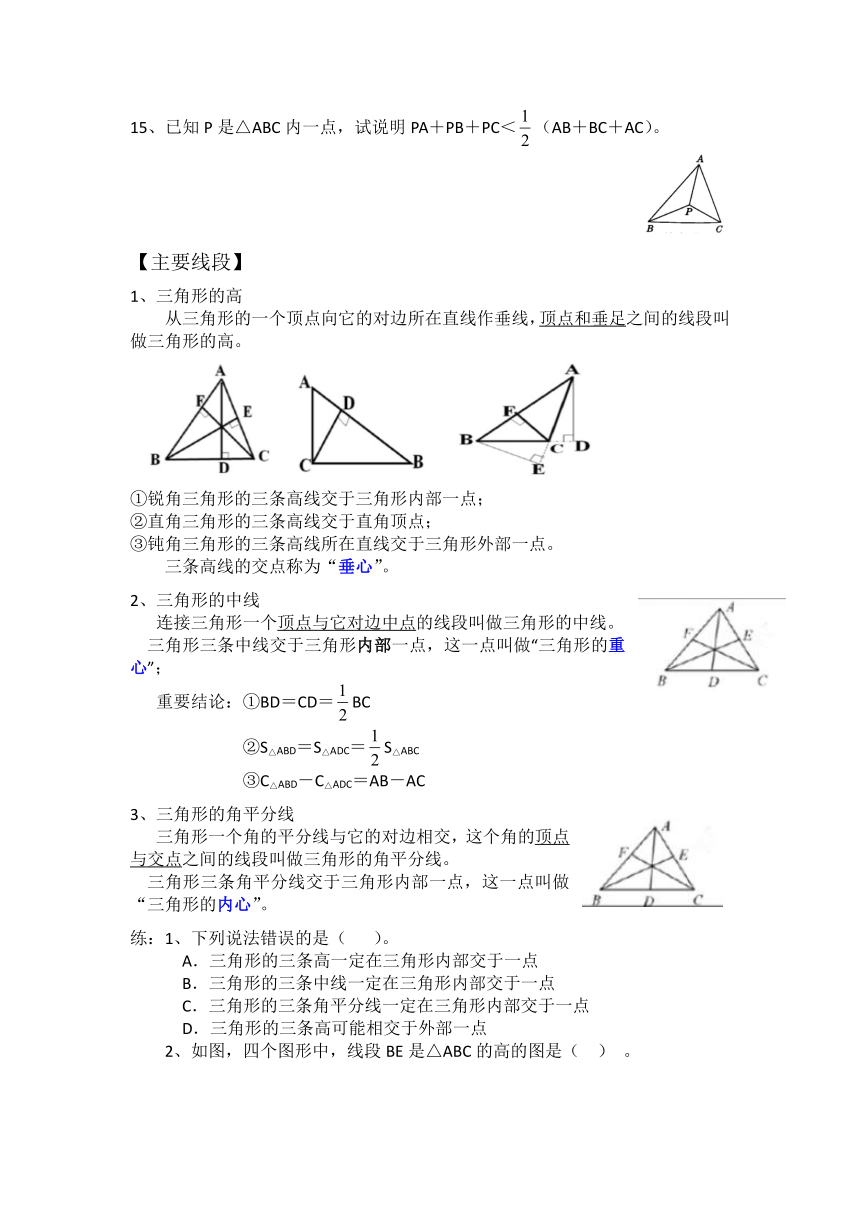
第十一章
三角形知识框架
【三角形的概念】
1、三角形的定义
由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形。
要点:①三条线段;②不在同一条直线上;③首尾顺次相连。
2、基本概念:三角形有三条边,
三个内角,
三个顶点。
边:组成三角形的线段,表示方法:AB(c)、BC(a)、AC(b)
内角:相邻两边所组成的角,表示方法:∠A、∠B、∠C
顶点:相邻两边的公共端点,表示方法:A、B、C
三角形
ABC用符号表示为△ABC。
夹边、夹角、对边、对角
3、数三角形个数技巧
1)按组成三角形的图形个数来数(如单个三角形、由2个图形组成的三角形……最后求和)
2)从图中的某一条线段开始,按一定的顺序找出能组成三角形的另外两条边;
3)先固定一个顶点,再变换另外两个顶点,找出不共线的三点共有多少组。
练:1、下列说法中正确的是(
)
由三个角组成的图形叫三角形
由三条直线组成图形叫三角形
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形
由三条线段组成的图形叫三角形
2、右图中三角形的个数是(
)
A、6
B、7
C、8
D、9
3、如右图所示:
(1)图中有几个三角形?把它们一一写出来。
(2)写出△ABD的三个内角。
(3)以∠C为内角的三角形有哪些?
(4)以AB为边的三角形有哪些?
【分类】
在等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
练:1、如果三角形的一个外角是锐角,则此三角形的形状是(
)
锐角三角形
B.钝角三角形
C.直角三角形
D.无法判断
2、若△ABC三边长分别为
m,n,p,且
|
m
-
n
|+(
n
-
p)2=
0
,则这个三角形为(
)
A、等腰三角形
B、等边三角形
C、直角三角形
D、等腰直角三角形
3、三角形中,若一个角等于其他两个角的差,则这个三角形是(
)
A.钝角三角形
B.直角三角形
C.锐角三角形
D.等腰三角形
4、根据下列所给条件,判断△ABC的形状(若已知的是角,则按角的分类标准去判断;若已知的是边,则按边的分类标准去判断)
(1)∠A=45°,∠B=65°,∠C=70°;
(2)∠C=90°;
(3)∠C=120°;
(4)AB=BC=4,AC=5.
【三边的关系】
①三角形任意两边之和大于第三边,b
+
c
>
a;
②三角形任意两边之差小于第三边,b
-
c
<
a。
理论依据:两点之间线段最短;
判断三条已知线段a、b、c能否组成三角形:
当a最长,且有
b
+
c
>
a时,就可构成三角形。
确定三角形第三边的取值范围:|a-b|
<
c
<
a+b
练:1、有下列长度的三条线段,能组成三角形的是(
)
A.2cm,3cm,4cm
B.1cm,
4cm,2cm
C
.
1cm,2cm,3cm
D.6cm,2cm,3cm
2、在下列长度的四根木棒中,能与3cm,7cm两根木棒围成一个三角形的是(
)
A.7cm
B.4cm
C.3cm
D
.10cm
3、一个三角形两边的长分别为
5
和
3,第三边的长是整数,且周长是偶数,则第三边的长是(
)
A、2
或
4
B
、4
或
6
C
、4
D
、2
或
6
4、一个三角形的两边长分别为
3
和
7,且第三边长为整数,这样的三角形的周长最小值是(
)
A.14
B.15
C.16
D.17
5、三角形的三边长分别为5,1+2
x
,8,则
x的取值范围是
________
。
6、等腰三角形
ABC的两边长为
2,4,则三角形
ABC的周长是
________
。
7、等腰三角形
ABC的两边长为
3,5,则三角形
ABC的周长是
________
。
8、长为11,8,6,4
的四根木条,选其中三根组成三角形有
种选法。
9、已知
a,b,c
是三角形的三边长,化简|a-b+c|+|a-b-c|
10、已知a,b,c为△ABC的三边长,且b、c满足,且a为方程|a-3|=2的解,求△ABC的周长,并判断△ABC的形状
11、已知等腰三角形的周长为16,
①已知一条边长为4,求另外两条边长;
②若三边长都为整数,求三角形各条边的长。
12、已知三角形的周长为12,三边长都为整数,判断三角形三边的长度及形状。
13、已知在△ABC中,三边长a,b,c都是整数,且满足a>b>c,a=8,那么满足条件的三角形共有多少个?
14、如图所示,D是△ABC内任意一点,连接BD、DC,试说明AB+AC>BD+CD。
15、已知P是△ABC内一点,试说明PA+PB+PC<(AB+BC+AC)。
【主要线段】
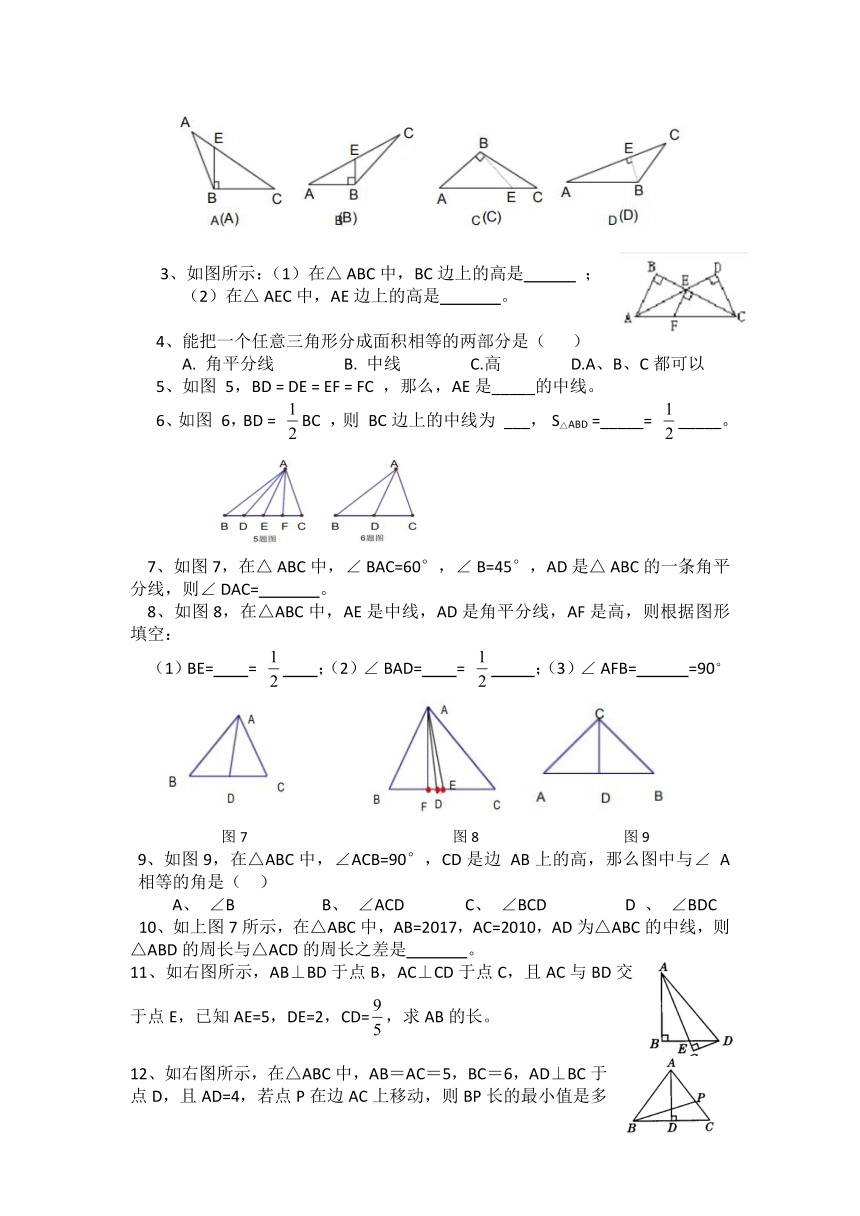
1、三角形的高
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高。
①锐角三角形的三条高线交于三角形内部一点;
②直角三角形的三条高线交于直角顶点;
③钝角三角形的三条高线所在直线交于三角形外部一点。
三条高线的交点称为“垂心”。
2、三角形的中线
连接三角形一个顶点与它对边中点的线段叫做三角形的中线。
三角形三条中线交于三角形内部一点,这一点叫做“三角形的重心”;
重要结论:①BD=CD=BC
②S△ABD=S△ADC=S△ABC
③C△ABD-C△ADC=AB-AC
3、三角形的角平分线
三角形一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
三角形三条角平分线交于三角形内部一点,这一点叫做“三角形的内心”。
练:1、下列说法错误的是(
)。
A.三角形的三条高一定在三角形内部交于一点
B.三角形的三条中线一定在三角形内部交于一点
C.三角形的三条角平分线一定在三角形内部交于一点
D.三角形的三条高可能相交于外部一点
2、如图,四个图形中,线段BE是△ABC的高的图是(
)
。
3、如图所示:(1)在△
ABC中,BC边上的高是
;
(2)在△
AEC中,AE边上的高是
。
4、能把一个任意三角形分成面积相等的两部分是(
)
A.
角平分线
B.
中线
C.高
D.A、B、C都可以
5、如图
5,BD
=
DE
=
EF
=
FC
,那么,AE是_____的中线。
6、如图
6,BD
=
BC
,则
BC边上的中线为
___,
S△ABD
=_____=
_____。
7、如图7,在△
ABC中,∠
BAC=60°,∠
B=45°,AD是△
ABC的一条角平分线,则∠
DAC=
。
8、如图8,在△ABC中,AE是中线,AD是角平分线,AF是高,则根据图形填空:
(1)BE=
=
;(2)∠
BAD=
=
;(3)∠
AFB=
=90°
图7
图8
图9
如图9,在△ABC中,∠ACB=90°,CD是边
AB上的高,那么图中与∠
A相等的角是(
)
A、
∠B
B、
∠ACD
C、
∠BCD
D
、
∠BDC
10、如上图7所示,在△ABC中,AB=2017,AC=2010,AD为△ABC的中线,则△ABD的周长与△ACD的周长之差是
。
11、如右图所示,AB⊥BD于点B,AC⊥CD于点C,且AC与BD交于点E,已知AE=5,DE=2,CD=,求AB的长。
12、如右图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP长的最小值是多少。
13、如右图所示,在△ABC中,D、E分别为BC、AD的中点,且△ABC的面积为4,则图中阴影部分的面积是
。
【稳定性】
1.
三角形具有稳定性。
2.
四边形及多边形不具有稳定性。
练:1.
桥梁拉杆,电视塔底座,都是三角形结构,这是利用三角形的
性
。
2、下列图形中具有稳定性的有(
)
A
、正方形
B
、长方形
C
、梯形
D
、
直角三角形
【三角形的内角】
三角形的内角和定理:三角形的内角和等于180°。
推论:①直角三角形的两个锐角互余;
②有两个角互余的三角形是直角三角形。
③三角形中至少有2个锐角;
④三角形中最多有1个钝角。
证明过程:
一、作CM
∥AB,则∠4=∠1,而∠
2+∠3+∠4=180°,即∠
A+
∠B+∠ACB=180°
二、作MN∥BC,则∠2=∠B,∠3=∠C,而∠
1+∠2+∠3=180°,即∠
BAC+∠B+∠
C=180°
注意:(1)证明的思路很多,基本思想是组成平角
(2)应用内角和定理可解决已知二个角求第三个角或已知三角关系求三个角
。
练:1、如图,在△ABC
中,AD平分∠BAC
且与BC相交于点D,∠B
=
40°,∠BAD=
30°,则∠C的度数是(
)
A.70°
B.80°
C.100°
D.110°
2、如图,已知∠A=∠30°,∠BEF=105°,∠B=20°,则∠D
=
(
)
A.25°
B.35°
C.45°
D.30
3、已知△
ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于
E,∠A=60°,∠C=80°。求:△BDE各内角的度数
。
4.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠A=60°,∠C=70°,求∠CAD,∠BOA的度数。
5、已知△ABC的三个内角的度数之比∠A:∠B:∠C=1:3:5,则∠B=
,∠C=
。
6、一个三角形三个内角的度数之比为2
:3:
7,这个三角形一定是(
)
7、在△ABC中,∠A+∠B=90°,∠C=3∠B,则∠A=
,∠B=
,∠C=
。
8、如图所示,在△ABC中,∠B=38°,∠C=54°,AE是BC边上的高,AD是∠BAC的平分线,求∠DAE的度数。
【三角形的外角】
定义:三角形一边与另一边的延长线组成的角,叫做三角形的外角
每个顶点处都有两个外角,但这两个外角是对顶角。
如
:
∠ACD、∠
BCE都是△ACB的外角,且∠
ACD=∠BCE。
所以说一个三角形有六个外角,但我们每一个顶点处只选一个外角,这样三角形的外角就只有三个了。
三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和。
练:1、如图6,若∠A=22°,∠B=45°,∠C=38°,则∠DFE等于
(
)
。
2、如图7,∠1=______
。
3、如图
8,则∠
1=______,∠
2=______,∠
3=______
4、已知等腰三角形的一个外角为150°,则它的底角为
___________
5、已知等腰三角形的一个外角是120°,则它是
(
)
A.
等腰直角三角形
B.
一般的等腰三角形
C.
等边三角形
D.
等腰钝角三角形
6、如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外角相邻的内角的度数为(
)
A.
30°
B.
60°
C.
90°
D.
120
°
7、已知三角形的三个外角的度数比为2∶3∶4,则它的最大内角的度数(
)
A.
90°
B.
110°
C.
100°
D.
120°
8、若一个三角形的三个内角的度数之比为1:2:3,那么相对应的三个外角的度数之比为(
)
A.
3:2:1
B.
1:2:3
C.3:4:5
D.5
:4:
3
9、如图,在△
ABC中,∠C=90°,外角∠EAB,∠ABF的平分线AD、BD相交于点D,求∠D的度数。
10、在△ABC中,∠A=40°,
D是BC延长线上一点,∠ABC的平分线与∠ACD的平分线交于E,求∠E的度数。
【中考链接】
1、已知
:
如图,∠
DAC是△
ABC的一个外角,∠
DAC=85°,∠B=45°,则∠
C的度数为(
)
A.50°
B.
45°
C.40°
D.
35°
2、等腰三角形的一个外角为100°,则这个等腰三角形的顶角的度数为
度。
3、如图,点D是△
ABC的边BC延长线上的一点,∠
A=70°,∠
ACD=105°,则∠
B=
。
4、如图,在△
ABC中,∠
A=50°,∠ABC=70°
,BD平分∠
ABC,则∠
BDC的度数是(
)。
A.
85
°
B.
80
°
C.
75
°
D.
70
°
【多边形及其内角和】
1.
多边形的概念
在平面中,由一些线段首尾顺次相接组成的图形叫做多边形,
多边形中相邻两边组成的角叫做它的内角,
多边
形的边与它邻边的延长线组成的角叫做它的外角。
连接多边形不相邻的两个顶点的线段叫做多边形的对角线。
一个n边形从一个顶点出发的对角线的条数为(n-3)条,其所有的对角线条数为:
。
2、内角和
(n-2)?180
°(n≥3且n为整数)
推导过程:
从
n
边形的一个顶点出发,向自身和相邻的两个顶点无法引对角线,向其他顶点共引(n-3)条对角线,这时n边形被分割成(n-2)个三角形,因为每个三角形的内角和是180°,所以
n
边形的内角和为:
(n-2)
·180°
3、外角和
多边形的外角和恒等于360度.
推导过程:
多边形的每个外角与相应的内角互补,共有n个外角,所以n边形的外角和为:n·180°-
(n-2)
·180°=
360°
4、实现镶嵌的条件:拼接在同一点的各个角的和恰好等于360°;
相邻的多边形有公共边。
练:1、六边形的对角线的条数是(
)
A.7
B.8
C.9
D.10
2、下列不能够镶嵌的正多边形组合是(
)
A.正三角形与正六边形
B.
正方形与正六边形
C.正三角形与正方形
D.
正五边形与正十边形
3、一些大小、形状完全相同的三角形_______密铺地板,正五边形
_______密铺地板(填“能”或“不能”)
4、一个多边形的边数增加一倍,它的内角和增加(
)
A.
180°
B.
360°
C.
(n-2)·180°
D.
n·
180
5、一个多边形内角和是1080°,则这个多边形的边数为
(
)
A、6
B、7
C、8
D、9
6、一个多边形的内角和等于它的外角和,这个多边形是(
)
A、三角形
B、四边形
C、五边形
D、六边形
7、一个多边形的内角和是外角和的2倍,则它是(
)
A、四边形
B、五边形
C、六边形
D、八边形
8、若一个多边形的内角和与外角和相加是1800°,则此多边形是(
)
A、八边形
B、十边形
C、十二边形
D、十四边形
9、一个多边形的每一个外角都是60°,那么这个多边形是(
)
A、正方形
B、正三角形
C、六边形
D、正六边形
10、.一个多边形的内角和比它的外角的和的2倍还大
180°,这个多边形的边数是(
)
A.5
B.6
C.7
D.8
10、一个多边形的内角和与外角和之比是5∶2,则这个多边形的边数为______。
11.将一个三角形截去一个角后,所形成的一个新的多边形的内角和是
。
12、(1)若多边形的内角和为
2340°,求此多边形的边数;
(2)一个多边形的每个外角都相等,如果它的内角与外角的度数之比为13:2,求这个多边形的边数。
(3)若四边形的四个外角的度数之比为1:2:3:4,求它的四个内角的度数。
13、正六边形共有____条对角线,内角和等于____,每一个内角等于
。
14.如果一个多边形的每一外角都是24°,那么它是
______边形
15.多边形的每一个内角都等于150°,则从此多边形一个顶点出发引出的对角线有
条
16.如果一个正多边形的每个内角是每个外角的3倍,那么它是
_____边形。
17、已知一个多边形少加一个内角的内角和是1125°,求这个多边形的边数。
18、如右图所示,小华从A点出发,沿直线前进10m后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点是,一共走的路程是(
)
A、140m
B、150m
C、160m
D、240m
19、如右图所示,求∠A+∠ABC+∠C+∠D+∠E+∠EFG+∠G的度数。
三角形知识框架
【三角形的概念】
1、三角形的定义
由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形。
要点:①三条线段;②不在同一条直线上;③首尾顺次相连。
2、基本概念:三角形有三条边,
三个内角,
三个顶点。
边:组成三角形的线段,表示方法:AB(c)、BC(a)、AC(b)
内角:相邻两边所组成的角,表示方法:∠A、∠B、∠C
顶点:相邻两边的公共端点,表示方法:A、B、C
三角形
ABC用符号表示为△ABC。
夹边、夹角、对边、对角
3、数三角形个数技巧
1)按组成三角形的图形个数来数(如单个三角形、由2个图形组成的三角形……最后求和)
2)从图中的某一条线段开始,按一定的顺序找出能组成三角形的另外两条边;
3)先固定一个顶点,再变换另外两个顶点,找出不共线的三点共有多少组。
练:1、下列说法中正确的是(
)
由三个角组成的图形叫三角形
由三条直线组成图形叫三角形
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形
由三条线段组成的图形叫三角形
2、右图中三角形的个数是(
)
A、6
B、7
C、8
D、9
3、如右图所示:
(1)图中有几个三角形?把它们一一写出来。
(2)写出△ABD的三个内角。
(3)以∠C为内角的三角形有哪些?
(4)以AB为边的三角形有哪些?
【分类】
在等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
练:1、如果三角形的一个外角是锐角,则此三角形的形状是(
)
锐角三角形
B.钝角三角形
C.直角三角形
D.无法判断
2、若△ABC三边长分别为
m,n,p,且
|
m
-
n
|+(
n
-
p)2=
0
,则这个三角形为(
)
A、等腰三角形
B、等边三角形
C、直角三角形
D、等腰直角三角形
3、三角形中,若一个角等于其他两个角的差,则这个三角形是(
)
A.钝角三角形
B.直角三角形
C.锐角三角形
D.等腰三角形
4、根据下列所给条件,判断△ABC的形状(若已知的是角,则按角的分类标准去判断;若已知的是边,则按边的分类标准去判断)
(1)∠A=45°,∠B=65°,∠C=70°;
(2)∠C=90°;
(3)∠C=120°;
(4)AB=BC=4,AC=5.
【三边的关系】
①三角形任意两边之和大于第三边,b
+
c
>
a;
②三角形任意两边之差小于第三边,b
-
c
<
a。
理论依据:两点之间线段最短;
判断三条已知线段a、b、c能否组成三角形:
当a最长,且有
b
+
c
>
a时,就可构成三角形。
确定三角形第三边的取值范围:|a-b|
<
c
<
a+b
练:1、有下列长度的三条线段,能组成三角形的是(
)
A.2cm,3cm,4cm
B.1cm,
4cm,2cm
C
.
1cm,2cm,3cm
D.6cm,2cm,3cm
2、在下列长度的四根木棒中,能与3cm,7cm两根木棒围成一个三角形的是(
)
A.7cm
B.4cm
C.3cm
D
.10cm
3、一个三角形两边的长分别为
5
和
3,第三边的长是整数,且周长是偶数,则第三边的长是(
)
A、2
或
4
B
、4
或
6
C
、4
D
、2
或
6
4、一个三角形的两边长分别为
3
和
7,且第三边长为整数,这样的三角形的周长最小值是(
)
A.14
B.15
C.16
D.17
5、三角形的三边长分别为5,1+2
x
,8,则
x的取值范围是
________
。
6、等腰三角形
ABC的两边长为
2,4,则三角形
ABC的周长是
________
。
7、等腰三角形
ABC的两边长为
3,5,则三角形
ABC的周长是
________
。
8、长为11,8,6,4
的四根木条,选其中三根组成三角形有
种选法。
9、已知
a,b,c
是三角形的三边长,化简|a-b+c|+|a-b-c|
10、已知a,b,c为△ABC的三边长,且b、c满足,且a为方程|a-3|=2的解,求△ABC的周长,并判断△ABC的形状
11、已知等腰三角形的周长为16,
①已知一条边长为4,求另外两条边长;
②若三边长都为整数,求三角形各条边的长。
12、已知三角形的周长为12,三边长都为整数,判断三角形三边的长度及形状。
13、已知在△ABC中,三边长a,b,c都是整数,且满足a>b>c,a=8,那么满足条件的三角形共有多少个?
14、如图所示,D是△ABC内任意一点,连接BD、DC,试说明AB+AC>BD+CD。
15、已知P是△ABC内一点,试说明PA+PB+PC<(AB+BC+AC)。
【主要线段】
1、三角形的高
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高。
①锐角三角形的三条高线交于三角形内部一点;
②直角三角形的三条高线交于直角顶点;
③钝角三角形的三条高线所在直线交于三角形外部一点。
三条高线的交点称为“垂心”。
2、三角形的中线
连接三角形一个顶点与它对边中点的线段叫做三角形的中线。
三角形三条中线交于三角形内部一点,这一点叫做“三角形的重心”;
重要结论:①BD=CD=BC
②S△ABD=S△ADC=S△ABC
③C△ABD-C△ADC=AB-AC
3、三角形的角平分线
三角形一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
三角形三条角平分线交于三角形内部一点,这一点叫做“三角形的内心”。
练:1、下列说法错误的是(
)。
A.三角形的三条高一定在三角形内部交于一点
B.三角形的三条中线一定在三角形内部交于一点
C.三角形的三条角平分线一定在三角形内部交于一点
D.三角形的三条高可能相交于外部一点
2、如图,四个图形中,线段BE是△ABC的高的图是(
)
。
3、如图所示:(1)在△
ABC中,BC边上的高是
;
(2)在△
AEC中,AE边上的高是
。
4、能把一个任意三角形分成面积相等的两部分是(
)
A.
角平分线
B.
中线
C.高
D.A、B、C都可以
5、如图
5,BD
=
DE
=
EF
=
FC
,那么,AE是_____的中线。
6、如图
6,BD
=
BC
,则
BC边上的中线为
___,
S△ABD
=_____=
_____。
7、如图7,在△
ABC中,∠
BAC=60°,∠
B=45°,AD是△
ABC的一条角平分线,则∠
DAC=
。
8、如图8,在△ABC中,AE是中线,AD是角平分线,AF是高,则根据图形填空:
(1)BE=
=
;(2)∠
BAD=
=
;(3)∠
AFB=
=90°
图7
图8
图9
如图9,在△ABC中,∠ACB=90°,CD是边
AB上的高,那么图中与∠
A相等的角是(
)
A、
∠B
B、
∠ACD
C、
∠BCD
D
、
∠BDC
10、如上图7所示,在△ABC中,AB=2017,AC=2010,AD为△ABC的中线,则△ABD的周长与△ACD的周长之差是
。
11、如右图所示,AB⊥BD于点B,AC⊥CD于点C,且AC与BD交于点E,已知AE=5,DE=2,CD=,求AB的长。
12、如右图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP长的最小值是多少。
13、如右图所示,在△ABC中,D、E分别为BC、AD的中点,且△ABC的面积为4,则图中阴影部分的面积是
。
【稳定性】
1.
三角形具有稳定性。
2.
四边形及多边形不具有稳定性。
练:1.
桥梁拉杆,电视塔底座,都是三角形结构,这是利用三角形的
性
。
2、下列图形中具有稳定性的有(
)
A
、正方形
B
、长方形
C
、梯形
D
、
直角三角形
【三角形的内角】
三角形的内角和定理:三角形的内角和等于180°。
推论:①直角三角形的两个锐角互余;
②有两个角互余的三角形是直角三角形。
③三角形中至少有2个锐角;
④三角形中最多有1个钝角。
证明过程:
一、作CM
∥AB,则∠4=∠1,而∠
2+∠3+∠4=180°,即∠
A+
∠B+∠ACB=180°
二、作MN∥BC,则∠2=∠B,∠3=∠C,而∠
1+∠2+∠3=180°,即∠
BAC+∠B+∠
C=180°
注意:(1)证明的思路很多,基本思想是组成平角
(2)应用内角和定理可解决已知二个角求第三个角或已知三角关系求三个角
。
练:1、如图,在△ABC
中,AD平分∠BAC
且与BC相交于点D,∠B
=
40°,∠BAD=
30°,则∠C的度数是(
)
A.70°
B.80°
C.100°
D.110°
2、如图,已知∠A=∠30°,∠BEF=105°,∠B=20°,则∠D
=
(
)
A.25°
B.35°
C.45°
D.30
3、已知△
ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于
E,∠A=60°,∠C=80°。求:△BDE各内角的度数
。
4.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠A=60°,∠C=70°,求∠CAD,∠BOA的度数。
5、已知△ABC的三个内角的度数之比∠A:∠B:∠C=1:3:5,则∠B=
,∠C=
。
6、一个三角形三个内角的度数之比为2
:3:
7,这个三角形一定是(
)
7、在△ABC中,∠A+∠B=90°,∠C=3∠B,则∠A=
,∠B=
,∠C=
。
8、如图所示,在△ABC中,∠B=38°,∠C=54°,AE是BC边上的高,AD是∠BAC的平分线,求∠DAE的度数。
【三角形的外角】
定义:三角形一边与另一边的延长线组成的角,叫做三角形的外角
每个顶点处都有两个外角,但这两个外角是对顶角。
如
:
∠ACD、∠
BCE都是△ACB的外角,且∠
ACD=∠BCE。
所以说一个三角形有六个外角,但我们每一个顶点处只选一个外角,这样三角形的外角就只有三个了。
三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和。
练:1、如图6,若∠A=22°,∠B=45°,∠C=38°,则∠DFE等于
(
)
。
2、如图7,∠1=______
。
3、如图
8,则∠
1=______,∠
2=______,∠
3=______
4、已知等腰三角形的一个外角为150°,则它的底角为
___________
5、已知等腰三角形的一个外角是120°,则它是
(
)
A.
等腰直角三角形
B.
一般的等腰三角形
C.
等边三角形
D.
等腰钝角三角形
6、如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外角相邻的内角的度数为(
)
A.
30°
B.
60°
C.
90°
D.
120
°
7、已知三角形的三个外角的度数比为2∶3∶4,则它的最大内角的度数(
)
A.
90°
B.
110°
C.
100°
D.
120°
8、若一个三角形的三个内角的度数之比为1:2:3,那么相对应的三个外角的度数之比为(
)
A.
3:2:1
B.
1:2:3
C.3:4:5
D.5
:4:
3
9、如图,在△
ABC中,∠C=90°,外角∠EAB,∠ABF的平分线AD、BD相交于点D,求∠D的度数。
10、在△ABC中,∠A=40°,
D是BC延长线上一点,∠ABC的平分线与∠ACD的平分线交于E,求∠E的度数。
【中考链接】
1、已知
:
如图,∠
DAC是△
ABC的一个外角,∠
DAC=85°,∠B=45°,则∠
C的度数为(
)
A.50°
B.
45°
C.40°
D.
35°
2、等腰三角形的一个外角为100°,则这个等腰三角形的顶角的度数为
度。
3、如图,点D是△
ABC的边BC延长线上的一点,∠
A=70°,∠
ACD=105°,则∠
B=
。
4、如图,在△
ABC中,∠
A=50°,∠ABC=70°
,BD平分∠
ABC,则∠
BDC的度数是(
)。
A.
85
°
B.
80
°
C.
75
°
D.
70
°
【多边形及其内角和】
1.
多边形的概念
在平面中,由一些线段首尾顺次相接组成的图形叫做多边形,
多边形中相邻两边组成的角叫做它的内角,
多边
形的边与它邻边的延长线组成的角叫做它的外角。
连接多边形不相邻的两个顶点的线段叫做多边形的对角线。
一个n边形从一个顶点出发的对角线的条数为(n-3)条,其所有的对角线条数为:
。
2、内角和
(n-2)?180
°(n≥3且n为整数)
推导过程:
从
n
边形的一个顶点出发,向自身和相邻的两个顶点无法引对角线,向其他顶点共引(n-3)条对角线,这时n边形被分割成(n-2)个三角形,因为每个三角形的内角和是180°,所以
n
边形的内角和为:
(n-2)
·180°
3、外角和
多边形的外角和恒等于360度.
推导过程:
多边形的每个外角与相应的内角互补,共有n个外角,所以n边形的外角和为:n·180°-
(n-2)
·180°=
360°
4、实现镶嵌的条件:拼接在同一点的各个角的和恰好等于360°;
相邻的多边形有公共边。
练:1、六边形的对角线的条数是(
)
A.7
B.8
C.9
D.10
2、下列不能够镶嵌的正多边形组合是(
)
A.正三角形与正六边形
B.
正方形与正六边形
C.正三角形与正方形
D.
正五边形与正十边形
3、一些大小、形状完全相同的三角形_______密铺地板,正五边形
_______密铺地板(填“能”或“不能”)
4、一个多边形的边数增加一倍,它的内角和增加(
)
A.
180°
B.
360°
C.
(n-2)·180°
D.
n·
180
5、一个多边形内角和是1080°,则这个多边形的边数为
(
)
A、6
B、7
C、8
D、9
6、一个多边形的内角和等于它的外角和,这个多边形是(
)
A、三角形
B、四边形
C、五边形
D、六边形
7、一个多边形的内角和是外角和的2倍,则它是(
)
A、四边形
B、五边形
C、六边形
D、八边形
8、若一个多边形的内角和与外角和相加是1800°,则此多边形是(
)
A、八边形
B、十边形
C、十二边形
D、十四边形
9、一个多边形的每一个外角都是60°,那么这个多边形是(
)
A、正方形
B、正三角形
C、六边形
D、正六边形
10、.一个多边形的内角和比它的外角的和的2倍还大
180°,这个多边形的边数是(
)
A.5
B.6
C.7
D.8
10、一个多边形的内角和与外角和之比是5∶2,则这个多边形的边数为______。
11.将一个三角形截去一个角后,所形成的一个新的多边形的内角和是
。
12、(1)若多边形的内角和为
2340°,求此多边形的边数;
(2)一个多边形的每个外角都相等,如果它的内角与外角的度数之比为13:2,求这个多边形的边数。
(3)若四边形的四个外角的度数之比为1:2:3:4,求它的四个内角的度数。
13、正六边形共有____条对角线,内角和等于____,每一个内角等于
。
14.如果一个多边形的每一外角都是24°,那么它是
______边形
15.多边形的每一个内角都等于150°,则从此多边形一个顶点出发引出的对角线有
条
16.如果一个正多边形的每个内角是每个外角的3倍,那么它是
_____边形。
17、已知一个多边形少加一个内角的内角和是1125°,求这个多边形的边数。
18、如右图所示,小华从A点出发,沿直线前进10m后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点是,一共走的路程是(
)
A、140m
B、150m
C、160m
D、240m
19、如右图所示,求∠A+∠ABC+∠C+∠D+∠E+∠EFG+∠G的度数。
