人教版八年级数学上册教学设计:12.2 三角形全等的判定二(表格式)
文档属性
| 名称 | 人教版八年级数学上册教学设计:12.2 三角形全等的判定二(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 85.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 00:00:00 | ||
图片预览

文档简介
八年级数学上册教学设计
课题
12.2
三角形全等的判定二
教学
目标
1.知道“边角边”,会用“边角边”证明两个三角形全等
2、会把间接已知转化为直接的已知;知道“边边角”不能判定三角形全等.
3、通过探究三角形全等的条件,培养学生观察分析图形的能力及发现问题的能力。
教学
重点
寻求“边角边”的条件.知道是两边与夹角为SAS。
教学
难点
寻找判定三角形全等的条件。特别是夹角的条件
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、两边及其夹角分别对应相等的两个三角形全等吗?
1.画△ABC,使AB=4cm,∠A=
60°AC=5cm。
试一试:再换两条线段和一个角:
△ABC和△DEF中,AB=DE=3㎝,∠B=∠E=45°,BC=EF=4
㎝。则它们完全重合吗?即△ABC≌△DEF?
确认△ABC≌△DEF。
在△ABC和△AˊBˊCˊ中,已知AB=AˊBˊ,∠B=∠Bˊ,
BC=BˊCˊ,△ABC与△AˊBˊCˊ全等吗?
概括:“边角边”判定定理。
2.如图2,AB=AD,AC=AE,能添上一个条件证明出△ABC≌△ADE吗?
二、“边边角”两个三角形是否全等?
1.以3cm,4cm为三角形的两边,长度为3cm的边所对的角为45°,动手画一个三角形,把所画的三角形与同桌同学画的三角形进行比较,那么所有的三角形都全等吗?
结论:两边及其一边所对的角相等,两个三角形不一定全等。
三角形全等判定二:简称“边角边”或“SAS”
两边和它们的夹角分别相等的两个三角形全等。
3、小练笔:
在
中,
AO=__________
________=________
BO=______________
∴△ABC≌
(
)
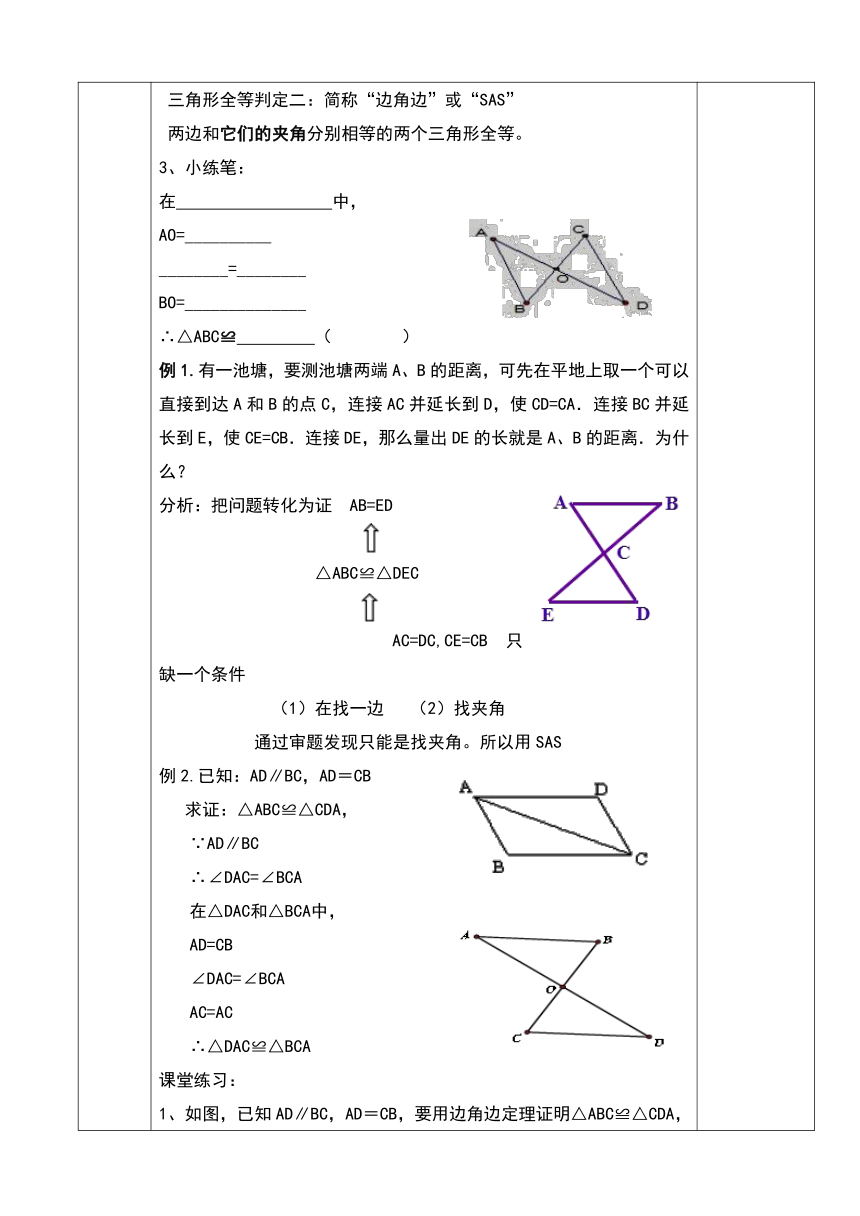
例1.有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?
分析:把问题转化为证
AB=ED
△ABC≌△DEC
AC=DC,CE=CB
只缺一个条件
(1)在找一边
(2)找夹角
通过审题发现只能是找夹角。所以用SAS
例2.已知:AD∥BC,AD=CB
求证:△ABC≌△CDA,
∵AD∥BC
∴∠DAC=∠BCA
在△DAC和△BCA中,
AD=CB
∠DAC=∠BCA
AC=AC
∴△DAC≌△BCA
课堂练习:
1、如图,已知AD∥BC,AD=CB,要用边角边定理证明△ABC≌△CDA,需要三个条件,这三个条件中,已具有两个条件,一是AD=CB(已知),二是
;
还需要一个条件
(这个条件可以
由已知中的条件
证得).
2、如图,在△DAB和△EAC中,AD=AE,AC=AB,∠1=∠2
求证:DB=EC
3、已知:点D分别是AD,BC的中点,求证:AB∥CD
4、如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,求证:∠A=∠D.
4、有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?
已知:AD∥BC,AD=CB
求证:△ABC≌△CDA,
6、已知:点D分别是AD,BC的中点,
求证:AB∥CD
板
书
设
计
三角形全等的判定二
教
学
反
思
课题
12.2
三角形全等的判定二
教学
目标
1.知道“边角边”,会用“边角边”证明两个三角形全等
2、会把间接已知转化为直接的已知;知道“边边角”不能判定三角形全等.
3、通过探究三角形全等的条件,培养学生观察分析图形的能力及发现问题的能力。
教学
重点
寻求“边角边”的条件.知道是两边与夹角为SAS。
教学
难点
寻找判定三角形全等的条件。特别是夹角的条件
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、两边及其夹角分别对应相等的两个三角形全等吗?
1.画△ABC,使AB=4cm,∠A=
60°AC=5cm。
试一试:再换两条线段和一个角:
△ABC和△DEF中,AB=DE=3㎝,∠B=∠E=45°,BC=EF=4
㎝。则它们完全重合吗?即△ABC≌△DEF?
确认△ABC≌△DEF。
在△ABC和△AˊBˊCˊ中,已知AB=AˊBˊ,∠B=∠Bˊ,
BC=BˊCˊ,△ABC与△AˊBˊCˊ全等吗?
概括:“边角边”判定定理。
2.如图2,AB=AD,AC=AE,能添上一个条件证明出△ABC≌△ADE吗?
二、“边边角”两个三角形是否全等?
1.以3cm,4cm为三角形的两边,长度为3cm的边所对的角为45°,动手画一个三角形,把所画的三角形与同桌同学画的三角形进行比较,那么所有的三角形都全等吗?
结论:两边及其一边所对的角相等,两个三角形不一定全等。
三角形全等判定二:简称“边角边”或“SAS”
两边和它们的夹角分别相等的两个三角形全等。
3、小练笔:
在
中,
AO=__________
________=________
BO=______________
∴△ABC≌
(
)
例1.有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?
分析:把问题转化为证
AB=ED
△ABC≌△DEC
AC=DC,CE=CB
只缺一个条件
(1)在找一边
(2)找夹角
通过审题发现只能是找夹角。所以用SAS
例2.已知:AD∥BC,AD=CB
求证:△ABC≌△CDA,
∵AD∥BC
∴∠DAC=∠BCA
在△DAC和△BCA中,
AD=CB
∠DAC=∠BCA
AC=AC
∴△DAC≌△BCA
课堂练习:
1、如图,已知AD∥BC,AD=CB,要用边角边定理证明△ABC≌△CDA,需要三个条件,这三个条件中,已具有两个条件,一是AD=CB(已知),二是
;
还需要一个条件
(这个条件可以
由已知中的条件
证得).
2、如图,在△DAB和△EAC中,AD=AE,AC=AB,∠1=∠2
求证:DB=EC
3、已知:点D分别是AD,BC的中点,求证:AB∥CD
4、如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,求证:∠A=∠D.
4、有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?
已知:AD∥BC,AD=CB
求证:△ABC≌△CDA,
6、已知:点D分别是AD,BC的中点,
求证:AB∥CD
板
书
设
计
三角形全等的判定二
教
学
反
思
