人教版九年级下册数学 28.2.2应用举例 同步练习(Word版 含解析)
文档属性
| 名称 | 人教版九年级下册数学 28.2.2应用举例 同步练习(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 200.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 00:00:00 | ||
图片预览




文档简介
28.2.2应用举例
同步练习
一.选择题
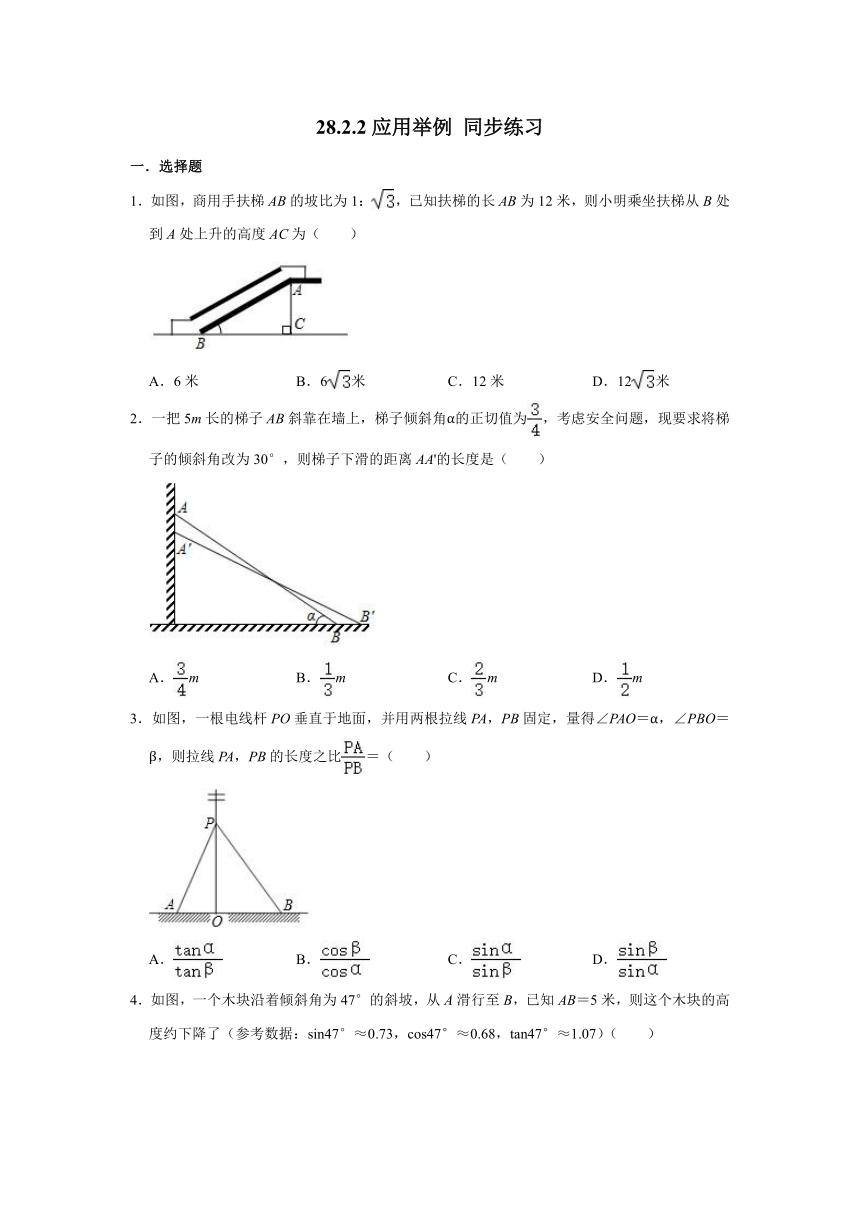
1.如图,商用手扶梯AB的坡比为1:,已知扶梯的长AB为12米,则小明乘坐扶梯从B处到A处上升的高度AC为( )
A.6米
B.6米
C.12米
D.12米
2.一把5m长的梯子AB斜靠在墙上,梯子倾斜角α的正切值为,考虑安全问题,现要求将梯子的倾斜角改为30°,则梯子下滑的距离AA'的长度是( )
A.m
B.m
C.m
D.m
3.如图,一根电线杆PO垂直于地面,并用两根拉线PA,PB固定,量得∠PAO=α,∠PBO=β,则拉线PA,PB的长度之比=( )
A.
B.
C.
D.
4.如图,一个木块沿着倾斜角为47°的斜坡,从A滑行至B,已知AB=5米,则这个木块的高度约下降了(参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)( )
A.3.65米
B.3.40米
C.3.35米
D.3.55米
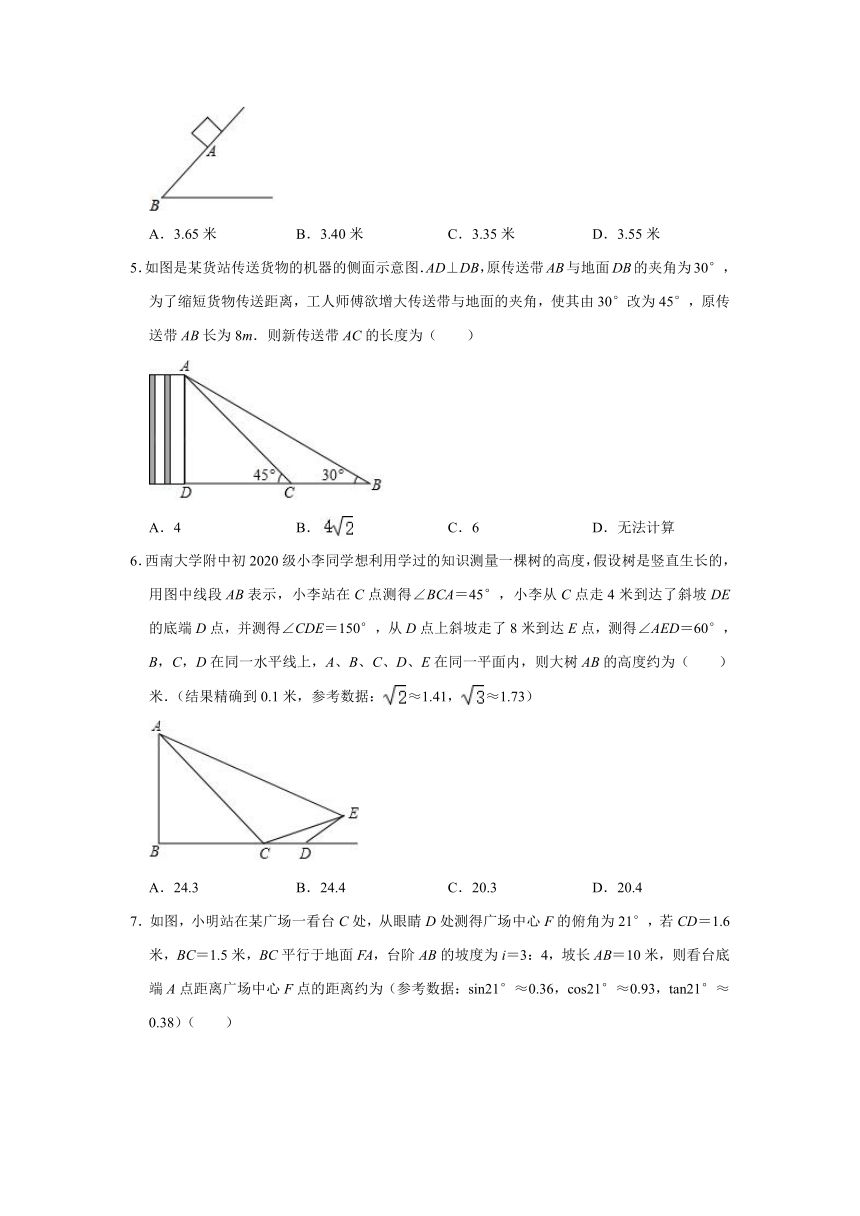
5.如图是某货站传送货物的机器的侧面示意图.AD⊥DB,原传送带AB与地面DB的夹角为30°,为了缩短货物传送距离,工人师傅欲增大传送带与地面的夹角,使其由30°改为45°,原传送带AB长为8m.则新传送带AC的长度为( )
A.4
B.
C.6
D.无法计算
6.西南大学附中初2020级小李同学想利用学过的知识测量一棵树的高度,假设树是竖直生长的,用图中线段AB表示,小李站在C点测得∠BCA=45°,小李从C点走4米到达了斜坡DE的底端D点,并测得∠CDE=150°,从D点上斜坡走了8米到达E点,测得∠AED=60°,B,C,D在同一水平线上,A、B、C、D、E在同一平面内,则大树AB的高度约为( )米.(结果精确到0.1米,参考数据:≈1.41,≈1.73)
A.24.3
B.24.4
C.20.3
D.20.4
7.如图,小明站在某广场一看台C处,从眼睛D处测得广场中心F的俯角为21°,若CD=1.6米,BC=1.5米,BC平行于地面FA,台阶AB的坡度为i=3:4,坡长AB=10米,则看台底端A点距离广场中心F点的距离约为(参考数据:sin21°≈0.36,cos21°≈0.93,tan21°≈0.38)( )
A.8.8米
B.9.5米
C.10.5米
D.12米
8.山重水复的地形景观造就了网红重庆,如图,山坡AB的坡度i=1:2.4,坡上有一棵树BC,当太阳光线与水平线成68°沿斜坡照下时,在斜坡上的树影AB长为6.5米,则这棵树BC的高度为( )米.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.38,tan68°≈2.48)
A.12.4
B.12.3
C.14.8
D.14.9
9.如图已知斜坡AB长米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE.若修建的斜坡BE的坡度为3:1,休闲平台DE的长是( )米.
A.20
B.15
C.
D.
10.如图所示,老张利用国庆假日在某钓鱼场钓鱼,风平浪静时,鱼漂露出水面部分AB=6m,微风吹来时,假设铅锤P不动,鱼漂移动了一段距离BC,且顶端恰好与水面平齐(即PA=PC,水平线1与OC夹角a=8°(点A在OC上,则铅锤P处的水深h为( )(参考数据:sin8°=,cos8°=,tan8°=)
A.150cm
B.144cm
C.111cm
D.105cm
二.填空题
11.如图是一个仰卧起坐健身器侧面示意图,AC、BC是支架,OC是坐垫,OD为靠背(可绕点O旋转),OA=OD=900mm,∠BAC=20°,当α=40°时,点D到地面的距离为
mm.(sin20°=0.34,cos20°=0.94,tan20°=0.36,sin40°=0.64,cos40°=0.77)
12.如图,某景区门口的柱子上方挂着一块景点宣传牌CD,宣传牌的一侧用绳子AD和BC牵引着两排小风车,经过测量得到如下数据:AM=2米,AB=4米,∠MAD=45°,∠MBC=30°,则CD的长度约为
米.(≈1.73,结果精确到0.1米)
13.如图,修建的二滩水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i=1:2.5,则坝底宽AD=
m.
14.某居民楼紧挨一座山坡AB,经过地质人员勘测,当坡度不超过45°时,可以确保山体不滑坡,如图所示,已知AE∥BD,斜坡AB的坡角∠ABD=60°,为防止滑坡,现对山坡进行改造,改造后,斜坡BC与地面BD成45°角,AC=10米.则斜坡BC=
米.
15.某游乐场新推出一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度,其中斜坡轨道BC的坡度i=1:2,BC=12米,CD=8米,∠D=36°,(其中A,B,C,D均在平面内)则垂直升降电梯AB的高度约为
米.(精确到0.1米,参考数据tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)
三.解答题
16.如图,某商场门前的台阶高出地面0.8米,即CB=0.8米,现将此台阶改造成供轮椅行走的斜坡AC,并且设计斜坡的倾斜角∠A为10°.求斜坡AC的长.(结果精确到0.1m)
【参考数据:sin10°=0.17.cos10°=0.98,tan10°=0.18】
17.淮安华联商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯AB长为10m,坡角∠ABD为45°,改造后的斜坡式自动扶梯的坡角∠ACB为15°,改造后的斜坡式自动扶梯水平距离增加了BC,请你计算BC的长度.(结果精确到1m,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,≈1.41)
18.2019年12月23日,湖南省政府批准,全国“十三五”规划重大水利工程﹣﹣邵阳资水犬木塘水库,将于2020年开工建设,施工测绘中,饮水干渠需经过一座险峻的石山,如图所示,AB,BC表示需铺设的干渠引水管道,经测量,A,B,C所处位置的海拔AA1,BB1,CC1分别为62m,200m,550m.若管道AB与水平线AA2的夹角为30°,管道BC与水平线BB2夹角为45°,求管道AB和BC的总长度(结果保留根号).
参考答案、
一.选择题
1.解:∵商用手扶梯AB的坡比1:,
设AC=x米,则BC=x米,
∴AB===2x=12,
解得:x=6,
∴AC=6米,
故选:A.
2.解:如图,∵梯子倾斜角α的正切值为,
∴设AC=3k,BC=4k,
∴AB==5k=5,
∴k=1,
∴AC=3米,BC=4米,
∵A′B′=AB=5,∠A′B′C=30°,
∴A′C=A′B′=,
∴AA′=AC﹣A′C=3﹣=米,
故梯子下滑的距离AA'的长度是米,
故选:D.
3.解:如图,在直角△PAO中,∠POA=90°,∠PAO=α,则PA=.
如图,在直角△PBO中,∠POB=90°,∠PBO=β,则PB=.
所以==.
故选:D.
4.解:如图,过A点作水平面的垂线AC,垂足为C,则≈0.73,
故AC≈5×0.73=3.65(米),
故选:A.
5.解:在Rt△ABD中,AD=AB?sin30°=8×(米),
在Rt△ACD中,∵∠ACD=45°,
∴AC=AD=4m,
故选:B.
6.解:过E作EG⊥AB于G,EF⊥BD于F,
则BG=EF,EG=BF,
∵∠CDE=150°,
∴∠EDF=30°,
∵DE=8,
∴EF=DE=4,DF=4,
∴CF=CD+DF=4+4,
∵∠ABC=90°,∠ACB=45°,
∴AB=BC,
∴GE=BF=AB+4+4,AG=AB﹣4,
∵∠AED=60°,∠GED=∠EDF=30°,
∴∠AEG=30°,
∴tan30°===,
解得:AB=14+6≈24.4,
故选:B.
7.解:如图,作BM⊥FA交FA的延长线于M,延长DC交FA的延长线于N.
∵BM:AM=3:4,AB=10米,
∴BM=6(米),AM=8(米),
在Rt△DNF中,tan21°=,
∴=0.38,
∴FN≈20(米),
∴AF=FN﹣AM﹣MN=20﹣8﹣1.5≈10.5(米),
故选:C.
8.解:延长CB交AD于E.设BC=xm.
在Rt△ABE中,∵AB=6.5m,BE:AE=1:2.4,
∴AE=6(m),BE=2.5(m),
在Rt△ACE中,∵tan68°=,
∴2.48=,
∴x=12.38≈12.4,
∴BC=12.4(m),
故选:A.
9.解:延长DE交BC于H.
由题意BH:EH=3:1,
在Rt△ABC中,AB=60,∠BAC=45°,
∵BC=AC=60,
∵AD=DB,DH∥AC,
∴BH=CH=30,
∴DH=AC=30,
∴EH=10,DE=30﹣10=20,
故选:A.
10.解:∵l∥BC,∴∠ACB=α=8°,
在Rt△ABC中,∵tanα=,
∴BC==42(cm),
根据题意,得h2+422=(h+6)2,
∴h=144(cm).
故选:B.
二.填空题
11.解:连接AD,过点O作OH⊥AD于H,
∵OA=OD=900mm,OH⊥AD,α=40°
∴∠AOH=∠AOD=20°,AH=DH,
∵∠BAC=20°,
∴∠BAC=∠AOH,
∴OH∥AB,
∴AD⊥AB,
在Rt△AOH中,OA=900mm,sin∠AOH=,
∴AH=OA?sin20°=900×0.34=306
(mm),
∴AD=2AH=612(mm),
故答案为:612.
12.解:在Rt△AMD中,∠MAD=45°,
∴DM=AM?tan45°=2(m),
在Rt△BMC中,∠MBC=30°,
∴CM=BM?tan30°,
∵BM=AM+AB=2+4=6(m),
∴CM=6×≈3.46(m),
∴CD=CM﹣DM=3.46﹣2≈1.5(米),
答:警示牌的高CD为1.5米.
13.解:∵AB的坡度i=1:3,
∴tanA=,
∴=,
∵BE=23,
∴AE=69,
∵BC=6,
∴EF=6,
∵CD的坡度i′=1:2.5,
∴tanD==,
∴=,
∴DF=57.5,
∴AD=AE+EF+DF=69+6+57.5=132.5(m).
答:坝底宽AD的长是132.5m.
故答案为:132.5.
14.解:作AM⊥BD于点M,作CN⊥BD于点N,如右图所示,
∵∠ABD=60°,∠CBD=45°,
∴BN=,BM=,BC=,
∵CN=AM,AC=BN﹣BM,AC=10米,
∴BC=≈33.4米,
即斜坡BC的长是33.4米.
故答案为:33.4
15.解:如图,延长AB和DC相交于点E,
由斜坡轨道BC的坡度为i=1:2,得
BE:CE=1:2.
设BE=x米,CE=2x米.
在Rt△BCE中,由勾股定理,得
BE2+CE2=BC2,
即x2+(2x)2=(12)2,
解得x=12,
BE=12米,CE=24米,
DE=DC+CE=8+24=32米,
由tan36°≈0.73,得=0.73,
解得AE=0.73×32=23.36米.
由线段的和差,得
AB=AE﹣BE=23.36﹣12=11.36≈11.4米,
故答案为11.4.
三.解答题
16.解:在Rt△ABC中,sinA=,
∴AC===≈4.7(m),
答:斜坡AC的长约为4.7m.
17.解:在Rt△ABD中,∠ABD=45°,AB=10,
∴AD=BD=AB?sin∠ABD=10×=5≈7,
∵∠ACD=15°,tan∠ACD=,
∴CD≈≈≈26,
∴BC=CD﹣BD=26﹣7=19.
故BC的长度约为19米.
18.解:根据题意知,四边形AA1B1O和四边形BB1C1B2均为矩形,
∴OB1=AA1=62m,B2C1=BB1=200m,
∴BO=BB1﹣OB1=200﹣62=138m,CB2=CC1﹣B2C1=550﹣200=350m,
在Rt△AOB中,∠AOB=90°,∠BAO=30°,BO=138m,
∴AB=2BO=2×138=276m;
在Rt△CBB2中,∠CB2B=90°,∠CBB2=45°,CB2=350m,
∴BC=CB2=350,
∴AB+BC=(276+350)m,
即管道AB和BC的总长度为:(276+350)m.
同步练习
一.选择题
1.如图,商用手扶梯AB的坡比为1:,已知扶梯的长AB为12米,则小明乘坐扶梯从B处到A处上升的高度AC为( )
A.6米
B.6米
C.12米
D.12米
2.一把5m长的梯子AB斜靠在墙上,梯子倾斜角α的正切值为,考虑安全问题,现要求将梯子的倾斜角改为30°,则梯子下滑的距离AA'的长度是( )
A.m
B.m
C.m
D.m
3.如图,一根电线杆PO垂直于地面,并用两根拉线PA,PB固定,量得∠PAO=α,∠PBO=β,则拉线PA,PB的长度之比=( )
A.
B.
C.
D.
4.如图,一个木块沿着倾斜角为47°的斜坡,从A滑行至B,已知AB=5米,则这个木块的高度约下降了(参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)( )
A.3.65米
B.3.40米
C.3.35米
D.3.55米
5.如图是某货站传送货物的机器的侧面示意图.AD⊥DB,原传送带AB与地面DB的夹角为30°,为了缩短货物传送距离,工人师傅欲增大传送带与地面的夹角,使其由30°改为45°,原传送带AB长为8m.则新传送带AC的长度为( )
A.4
B.
C.6
D.无法计算
6.西南大学附中初2020级小李同学想利用学过的知识测量一棵树的高度,假设树是竖直生长的,用图中线段AB表示,小李站在C点测得∠BCA=45°,小李从C点走4米到达了斜坡DE的底端D点,并测得∠CDE=150°,从D点上斜坡走了8米到达E点,测得∠AED=60°,B,C,D在同一水平线上,A、B、C、D、E在同一平面内,则大树AB的高度约为( )米.(结果精确到0.1米,参考数据:≈1.41,≈1.73)
A.24.3
B.24.4
C.20.3
D.20.4
7.如图,小明站在某广场一看台C处,从眼睛D处测得广场中心F的俯角为21°,若CD=1.6米,BC=1.5米,BC平行于地面FA,台阶AB的坡度为i=3:4,坡长AB=10米,则看台底端A点距离广场中心F点的距离约为(参考数据:sin21°≈0.36,cos21°≈0.93,tan21°≈0.38)( )
A.8.8米
B.9.5米
C.10.5米
D.12米
8.山重水复的地形景观造就了网红重庆,如图,山坡AB的坡度i=1:2.4,坡上有一棵树BC,当太阳光线与水平线成68°沿斜坡照下时,在斜坡上的树影AB长为6.5米,则这棵树BC的高度为( )米.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.38,tan68°≈2.48)
A.12.4
B.12.3
C.14.8
D.14.9
9.如图已知斜坡AB长米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE.若修建的斜坡BE的坡度为3:1,休闲平台DE的长是( )米.
A.20
B.15
C.
D.
10.如图所示,老张利用国庆假日在某钓鱼场钓鱼,风平浪静时,鱼漂露出水面部分AB=6m,微风吹来时,假设铅锤P不动,鱼漂移动了一段距离BC,且顶端恰好与水面平齐(即PA=PC,水平线1与OC夹角a=8°(点A在OC上,则铅锤P处的水深h为( )(参考数据:sin8°=,cos8°=,tan8°=)
A.150cm
B.144cm
C.111cm
D.105cm
二.填空题
11.如图是一个仰卧起坐健身器侧面示意图,AC、BC是支架,OC是坐垫,OD为靠背(可绕点O旋转),OA=OD=900mm,∠BAC=20°,当α=40°时,点D到地面的距离为
mm.(sin20°=0.34,cos20°=0.94,tan20°=0.36,sin40°=0.64,cos40°=0.77)
12.如图,某景区门口的柱子上方挂着一块景点宣传牌CD,宣传牌的一侧用绳子AD和BC牵引着两排小风车,经过测量得到如下数据:AM=2米,AB=4米,∠MAD=45°,∠MBC=30°,则CD的长度约为
米.(≈1.73,结果精确到0.1米)
13.如图,修建的二滩水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i=1:2.5,则坝底宽AD=
m.
14.某居民楼紧挨一座山坡AB,经过地质人员勘测,当坡度不超过45°时,可以确保山体不滑坡,如图所示,已知AE∥BD,斜坡AB的坡角∠ABD=60°,为防止滑坡,现对山坡进行改造,改造后,斜坡BC与地面BD成45°角,AC=10米.则斜坡BC=
米.
15.某游乐场新推出一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度,其中斜坡轨道BC的坡度i=1:2,BC=12米,CD=8米,∠D=36°,(其中A,B,C,D均在平面内)则垂直升降电梯AB的高度约为
米.(精确到0.1米,参考数据tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)
三.解答题
16.如图,某商场门前的台阶高出地面0.8米,即CB=0.8米,现将此台阶改造成供轮椅行走的斜坡AC,并且设计斜坡的倾斜角∠A为10°.求斜坡AC的长.(结果精确到0.1m)
【参考数据:sin10°=0.17.cos10°=0.98,tan10°=0.18】
17.淮安华联商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯AB长为10m,坡角∠ABD为45°,改造后的斜坡式自动扶梯的坡角∠ACB为15°,改造后的斜坡式自动扶梯水平距离增加了BC,请你计算BC的长度.(结果精确到1m,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,≈1.41)
18.2019年12月23日,湖南省政府批准,全国“十三五”规划重大水利工程﹣﹣邵阳资水犬木塘水库,将于2020年开工建设,施工测绘中,饮水干渠需经过一座险峻的石山,如图所示,AB,BC表示需铺设的干渠引水管道,经测量,A,B,C所处位置的海拔AA1,BB1,CC1分别为62m,200m,550m.若管道AB与水平线AA2的夹角为30°,管道BC与水平线BB2夹角为45°,求管道AB和BC的总长度(结果保留根号).
参考答案、
一.选择题
1.解:∵商用手扶梯AB的坡比1:,
设AC=x米,则BC=x米,
∴AB===2x=12,
解得:x=6,
∴AC=6米,
故选:A.
2.解:如图,∵梯子倾斜角α的正切值为,
∴设AC=3k,BC=4k,
∴AB==5k=5,
∴k=1,
∴AC=3米,BC=4米,
∵A′B′=AB=5,∠A′B′C=30°,
∴A′C=A′B′=,
∴AA′=AC﹣A′C=3﹣=米,
故梯子下滑的距离AA'的长度是米,
故选:D.
3.解:如图,在直角△PAO中,∠POA=90°,∠PAO=α,则PA=.
如图,在直角△PBO中,∠POB=90°,∠PBO=β,则PB=.
所以==.
故选:D.
4.解:如图,过A点作水平面的垂线AC,垂足为C,则≈0.73,
故AC≈5×0.73=3.65(米),
故选:A.
5.解:在Rt△ABD中,AD=AB?sin30°=8×(米),
在Rt△ACD中,∵∠ACD=45°,
∴AC=AD=4m,
故选:B.
6.解:过E作EG⊥AB于G,EF⊥BD于F,
则BG=EF,EG=BF,
∵∠CDE=150°,
∴∠EDF=30°,
∵DE=8,
∴EF=DE=4,DF=4,
∴CF=CD+DF=4+4,
∵∠ABC=90°,∠ACB=45°,
∴AB=BC,
∴GE=BF=AB+4+4,AG=AB﹣4,
∵∠AED=60°,∠GED=∠EDF=30°,
∴∠AEG=30°,
∴tan30°===,
解得:AB=14+6≈24.4,
故选:B.
7.解:如图,作BM⊥FA交FA的延长线于M,延长DC交FA的延长线于N.
∵BM:AM=3:4,AB=10米,
∴BM=6(米),AM=8(米),
在Rt△DNF中,tan21°=,
∴=0.38,
∴FN≈20(米),
∴AF=FN﹣AM﹣MN=20﹣8﹣1.5≈10.5(米),
故选:C.
8.解:延长CB交AD于E.设BC=xm.
在Rt△ABE中,∵AB=6.5m,BE:AE=1:2.4,
∴AE=6(m),BE=2.5(m),
在Rt△ACE中,∵tan68°=,
∴2.48=,
∴x=12.38≈12.4,
∴BC=12.4(m),
故选:A.
9.解:延长DE交BC于H.
由题意BH:EH=3:1,
在Rt△ABC中,AB=60,∠BAC=45°,
∵BC=AC=60,
∵AD=DB,DH∥AC,
∴BH=CH=30,
∴DH=AC=30,
∴EH=10,DE=30﹣10=20,
故选:A.
10.解:∵l∥BC,∴∠ACB=α=8°,
在Rt△ABC中,∵tanα=,
∴BC==42(cm),
根据题意,得h2+422=(h+6)2,
∴h=144(cm).
故选:B.
二.填空题
11.解:连接AD,过点O作OH⊥AD于H,
∵OA=OD=900mm,OH⊥AD,α=40°
∴∠AOH=∠AOD=20°,AH=DH,
∵∠BAC=20°,
∴∠BAC=∠AOH,
∴OH∥AB,
∴AD⊥AB,
在Rt△AOH中,OA=900mm,sin∠AOH=,
∴AH=OA?sin20°=900×0.34=306
(mm),
∴AD=2AH=612(mm),
故答案为:612.
12.解:在Rt△AMD中,∠MAD=45°,
∴DM=AM?tan45°=2(m),
在Rt△BMC中,∠MBC=30°,
∴CM=BM?tan30°,
∵BM=AM+AB=2+4=6(m),
∴CM=6×≈3.46(m),
∴CD=CM﹣DM=3.46﹣2≈1.5(米),
答:警示牌的高CD为1.5米.
13.解:∵AB的坡度i=1:3,
∴tanA=,
∴=,
∵BE=23,
∴AE=69,
∵BC=6,
∴EF=6,
∵CD的坡度i′=1:2.5,
∴tanD==,
∴=,
∴DF=57.5,
∴AD=AE+EF+DF=69+6+57.5=132.5(m).
答:坝底宽AD的长是132.5m.
故答案为:132.5.
14.解:作AM⊥BD于点M,作CN⊥BD于点N,如右图所示,
∵∠ABD=60°,∠CBD=45°,
∴BN=,BM=,BC=,
∵CN=AM,AC=BN﹣BM,AC=10米,
∴BC=≈33.4米,
即斜坡BC的长是33.4米.
故答案为:33.4
15.解:如图,延长AB和DC相交于点E,
由斜坡轨道BC的坡度为i=1:2,得
BE:CE=1:2.
设BE=x米,CE=2x米.
在Rt△BCE中,由勾股定理,得
BE2+CE2=BC2,
即x2+(2x)2=(12)2,
解得x=12,
BE=12米,CE=24米,
DE=DC+CE=8+24=32米,
由tan36°≈0.73,得=0.73,
解得AE=0.73×32=23.36米.
由线段的和差,得
AB=AE﹣BE=23.36﹣12=11.36≈11.4米,
故答案为11.4.
三.解答题
16.解:在Rt△ABC中,sinA=,
∴AC===≈4.7(m),
答:斜坡AC的长约为4.7m.
17.解:在Rt△ABD中,∠ABD=45°,AB=10,
∴AD=BD=AB?sin∠ABD=10×=5≈7,
∵∠ACD=15°,tan∠ACD=,
∴CD≈≈≈26,
∴BC=CD﹣BD=26﹣7=19.
故BC的长度约为19米.
18.解:根据题意知,四边形AA1B1O和四边形BB1C1B2均为矩形,
∴OB1=AA1=62m,B2C1=BB1=200m,
∴BO=BB1﹣OB1=200﹣62=138m,CB2=CC1﹣B2C1=550﹣200=350m,
在Rt△AOB中,∠AOB=90°,∠BAO=30°,BO=138m,
∴AB=2BO=2×138=276m;
在Rt△CBB2中,∠CB2B=90°,∠CBB2=45°,CB2=350m,
∴BC=CB2=350,
∴AB+BC=(276+350)m,
即管道AB和BC的总长度为:(276+350)m.
