苏科版八年级上册数学 6.4用一次函数解决问题 同步练习(Word版 含解析)
文档属性
| 名称 | 苏科版八年级上册数学 6.4用一次函数解决问题 同步练习(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 118.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 07:50:31 | ||
图片预览



文档简介
6.4用一次函数解决问题
同步练习
一.选择题
1.如图,一长为5m,宽为2m的长方形木板,现要在长边上截去长为xm的一部分,则剩余木板的面积(空白部分)y(m2)与x(m)的函数关系式为(0≤x<5)( )
A.y=10﹣x
B.y=5x
C.y=2x
D.y=﹣2x+10
2.某公司市场营销部的个人收入y(元)与其每月的销售量x(万件)成一次函数关系,其图象如图所示,营销人员没有销售量时最低收入是( )
A.1000
B.2000
C.3000
D.4000
3.A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.下列说法错误的是( )
A.乙晚出发1小时
B.乙出发3小时后追上甲
C.甲的速度是4千米/小时
D.乙先到达B地
4.设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回,设x秒后两车间的距离为y米,y关于x的函数关系如图所示,则甲车的速度为( )
A.10米/秒
B.11米/秒
C.12米/秒
D.13米/秒
5.小明用刻度不超过100℃的温度计来估计某食用油的沸点温度:将该食用油倒入锅中,均匀加热,每隔10s测量一次锅中的油温,得到如下数据:
时间t(单位:S)
0
10
20
30
40
油温y(单位:℃)
10
30
50
70
90
当加热100s时,油沸腾了,则小明估计这种油的沸点温度是( )
A.150℃
B.170℃
C.190℃
D.210℃
6.小红从家出发去晨跑,她离家的距离y(米)与时间x(分)的关系图象如图所示.下列结论错误的是( )
A.出发10分钟时,小红距离家1000米
B.整个晨跑过程一共走了3600米
C.返回时速度为60米/分
D.去时的平均速度小于返回速度
7.如图,甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离为S(km)和行驶时间t(h)之间的函数关系的图象如图所示,则下列结论错误的是( )
A.A、B两地相距18km
B.甲在途中停留了0.5小时
C.全程行驶时间乙比甲少用了1小时
D.乙出发后0.5小时追上甲
8.A、B两地相距90km,甲、乙两人从两地出发相向而行,甲先出发.图中l1.l2表示两人离A地的距离s(km)与时间t(h)的关系,结合图象,下列结论错误的是( )
A.l1是表示甲离A地的距离与时间关系的图象
B.乙的速度是30km/h
C.两人相遇时间在t=1.2h
D.当甲到达终点时乙距离终点还有45km
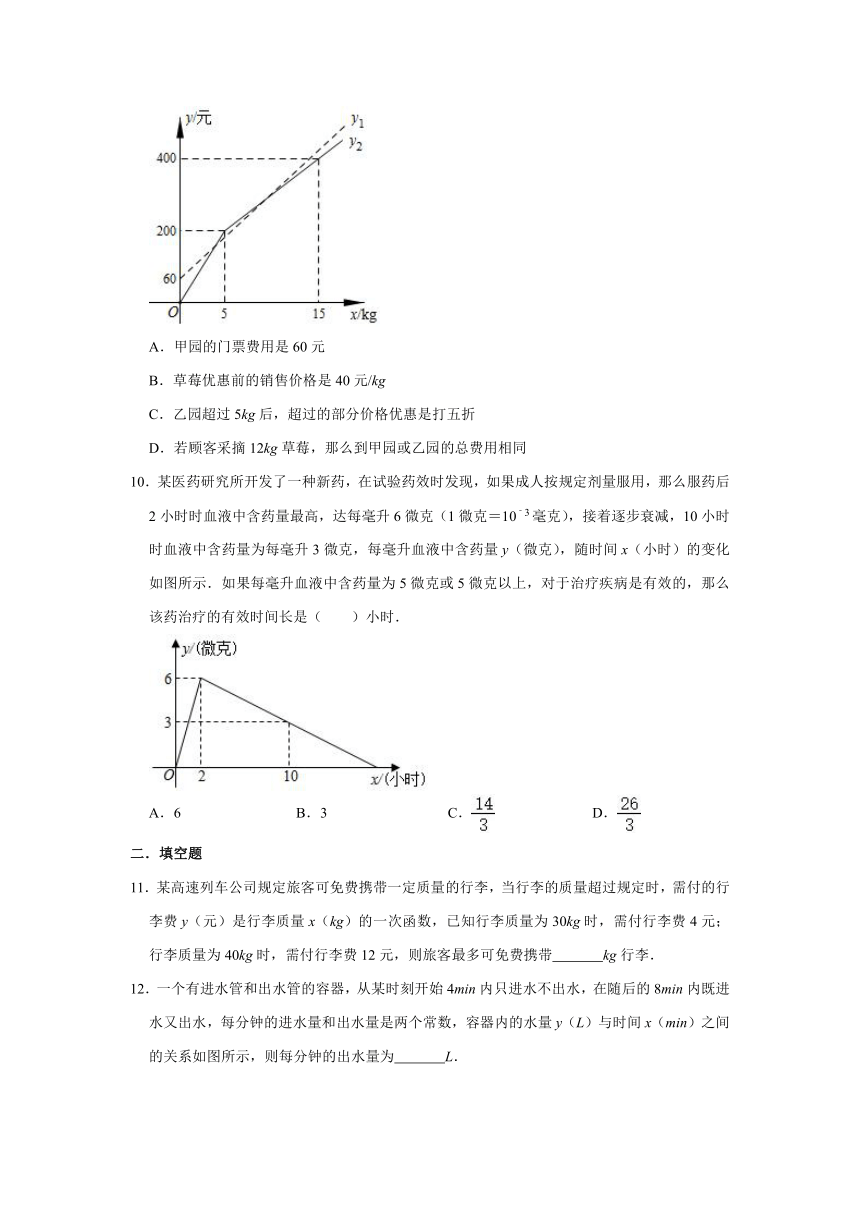
9.甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为xkg,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元.y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/kg
C.乙园超过5kg后,超过的部分价格优惠是打五折
D.若顾客采摘12kg草莓,那么到甲园或乙园的总费用相同
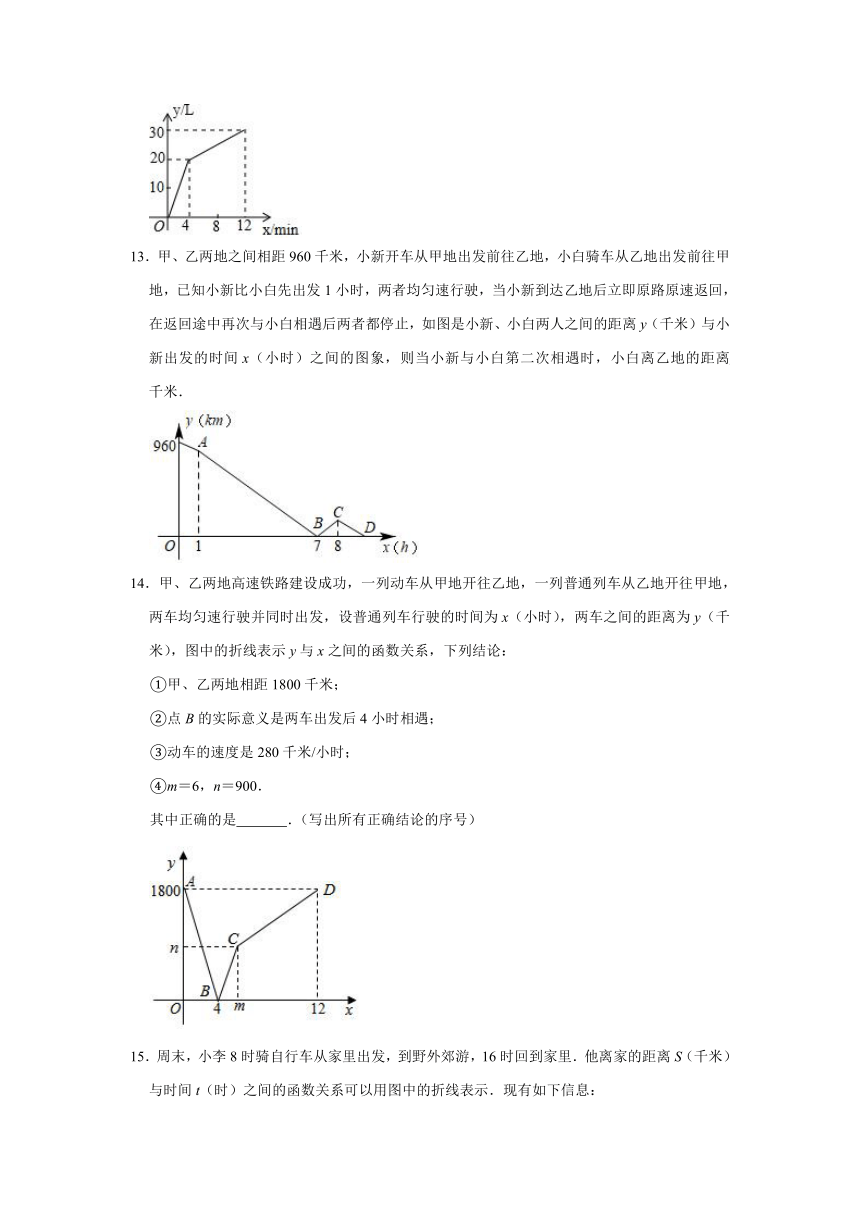
10.某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10﹣3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示.如果每毫升血液中含药量为5微克或5微克以上,对于治疗疾病是有效的,那么该药治疗的有效时间长是( )小时.
A.6
B.3
C.
D.
二.填空题
11.某高速列车公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,已知行李质量为30kg时,需付行李费4元;行李质量为40kg时,需付行李费12元,则旅客最多可免费携带
kg行李.
12.一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为
L.
13.甲、乙两地之间相距960千米,小新开车从甲地出发前往乙地,小白骑车从乙地出发前往甲地,已知小新比小白先出发1小时,两者均匀速行驶,当小新到达乙地后立即原路原速返回,在返回途中再次与小白相遇后两者都停止,如图是小新、小白两人之间的距离y(千米)与小新出发的时间x(小时)之间的图象,则当小新与小白第二次相遇时,小白离乙地的距离
千米.
14.甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,下列结论:
①甲、乙两地相距1800千米;
②点B的实际意义是两车出发后4小时相遇;
③动车的速度是280千米/小时;
④m=6,n=900.
其中正确的是
.(写出所有正确结论的序号)
15.周末,小李8时骑自行车从家里出发,到野外郊游,16时回到家里.他离家的距离S(千米)与时间t(时)之间的函数关系可以用图中的折线表示.现有如下信息:
(1)小李到达离家最远的地方的时间是14时;
(2)小李第一次休息时间是10时;
(3)11时到12时,小李骑了5千米;
(4)返回时,小李的平均车速是10千米/时.
其中,正确的信息有
(填序号).
三.解答题
16.一辆汽车在公路上匀速行驶,下表记录的是汽车在加满油后油箱内剩余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x(时)
0
1
2
剩余油量y(升)
100
80
60
(1)小明分析上表中所给的数据发现x,y成一次函数关系,试求出它们之间的函数表达式(不要求写出自变量的取值范围);
(2)求汽车行驶4.2小时后,油箱内剩余油多少升?
17.某社区的游泳馆按照顾客游泳的次数收取费用,每次的全票价为40元.在盛夏即将来临时,为吸引更多的顾客再次光顾,推出了以下两种收费方式.
方式一:先交250元会员费,每次游泳按照全票价的7.5折收取费用;
方式二:第一次收全票价,以后每次按照全票价的9.5折收取费用.
(1)按照方式一的总费用为y1,按照方式二的总费用为y2,请直接写出y1,y2与游泳次数x的函数关系式;
(2)去该游泳馆的次数等于
次时,两种方式收取总费用一样.
18.在近期“抗疫”期间,某药店销售A、B两种型号的口罩,已知销售80只A型和45只B型的利润为21元,销售40只A型和60只B型的利润为18元.
(1)求每只A型口罩和B型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不少于A型口罩的进货量且不超过它的3倍,设购进A型口罩x只,这2000只口罩的销售总利润为y元.
①求y关于x的函数关系式,并求出自变量x的取值范围;
②该药店购进A型、B型口罩各多少只,才能使销售总利润最大?
参考答案
一.选择题
1.解:由题意可得:y=2(5﹣x)
=10﹣2x.
故选:D.
2.解:设y与x的函数关系为y=kx+b,由题意得:
,
解得:,
∴y=5000x+2000,
当x=0时,
y=5000×0+2000=2000,
∴营销人员没有销售量时最低收入是2000元,
故选:B.
3.解:由图象可得,
乙晚出发1小时,故选项A正确;
乙出发3﹣1=2小时追上甲,故选项B错误;
甲的速度是12÷3=4(千米/小时),故选项C正确;
乙先到达B地,故选项D正确;
故选:B.
4.解:设甲车的速度为v1m/s,乙车的速度为v2m/s,
由图象可知:
开始时,乙车与甲车相距300米,
乙车用100秒追上了甲车,
∴100v1+300=100v2,
装完货物后,甲乙两车行驶了20秒后,两车相距500米,
∴20v1+20v2=500,
∴,
解得:,
故选:B.
5.解:设y=kt+b,
根据题意,得:,
解得,
∴y=2t+10,
当t=100时,y=2×100+10=210,
即当加热100s时,油沸腾了,小明估计这种油的沸点温度是210℃,
故选:D.
6.解:由图象可得:
x=10时y=1000,即出发10分钟时,小红距离家1000米,故本选项不合题意;
B.整个晨跑过程一共走了1800×2=3600(米),故本选项不合题意;
C.返回时速度为:1800÷(30﹣20)=180(米/分),故本选项符合题意;
D.去时的平均速度为:1800÷20=90(米/分),即去时的平均速度小于返回速度,故本选项不合题意.
故选:C.
7.解:A.由图可得,s为18千米,即A、B两地的距离是18千米,故A选项不合题意;
B.甲在0.5小时至1小时之间,S没有变化,说明甲在途中停留了0.5小时,故B选项不合题意;
C.由图可得,甲行驶的时间为2小时,乙行驶的时间为1.5小时,所以全程乙比甲少用了0.5小时,故C选项符合题意;
D.图中P点的实际意义是:甲,乙相遇,此时乙出发了0.5小时,故D选项不合题意.
故选:C.
8.解:∵甲先出发,
∴表示甲离A地的距离与时间关系的图象是l1,
故选项A不合题意;
乙的速度是:90÷(3.5﹣0.5)=90÷3=30(km/h),
故选项B不合题意;
设甲对应的函数解析式为y=ax+b,
,解得,
∴甲对应的函数解析式为y=﹣45x+90,
设乙对应的函数解析式为y=cx+d,
,解得,
即乙对应的函数解析式为y=30x﹣15,
,解得,
即甲出发1.4小时后两人相遇.
故选项C符合题意;
90﹣30×(2﹣0.5)=45(km),
即当甲到达终点时乙距离终点还有45km.
故选项D不符合题意.
故选:C.
9.解:由图象可得,
甲园的门票为60元,故选项A正确;
乙园草莓优惠前的销售价格是:200÷5=40(元/千克),故选项B正确;
=0.5,
即乙园超过5kg后,超过的部分价格优惠是打5折,故选项C正确;
若顾客采摘12kg草莓,甲园花费为:60+12×40×0.6=344(元),乙园的花费为:40×5+(12﹣5)×40×0.5=340(元),
∵344>340,
∴若顾客采摘12kg草莓,那么到甲园比到乙园的总费用高,故选项D错误;
故选:D.
10.解:当x≤2时,设y=k1x,
把(2,6)代入上式,得k1=3,
∴x≤2时,y=3x;
当x>2时,设y=k2x+b,把(2,6),(10,3)代入上式,
,解得,
∴y=;
把y=5代入y=3x,得x1=;
把y=5代入y=,得x2=,
则x2﹣x1=3小时.
即该药治疗的有效时间长是3小时.
故选:B.
二.填空题
11.解:设行李费y(元)与行李质量x(kg)的函数关系式为y=kx+b,
∵行李质量为30kg时,需付行李费4元;行李质量为40kg时,需付行李费12元,
∴,
解得,
即行李费y(元)与行李质量x(kg)的函数关系式为y=0.8x﹣20,
当y=0时,0=0.8x﹣20,解得x=25,
故答案为:25.
12.解:由图象可得,
每分钟的进水量为:20÷4=5(L),
每分钟的出水量为:5﹣(30﹣20)÷(12﹣4)=5﹣10÷8=5﹣1.25=3.75(L),
故答案为:3.75.
13.解:设小新的速度为akm/h,小白的速度为bkm/h,
根据题意得:,
解得,,
设第二次小新追上小白的时间为m小时,
120m﹣20(m﹣1)=960,
解得,m=9.4,
∴当小新与小白第二次相遇时,小白离乙地地的距离为:20×(9.4﹣1)=168(千米).
故答案为:168.
14.解:由图象可知,甲、乙两地相距1800千米,故①说法正确;
点B的实际意义是两车出发后4小时相遇,故②说法正确;
动车的速度为:1800÷4﹣150=300(km/h),故③说法错误;
150×4÷300+4=6,
∴m=6,n=150×6=900,
故④说法正确;
∴正确的是①②④.
故答案为:①②④.
15.解:由图象可得,
小李到达离家最远的地方的时间是14时,故(1)正确;
小李第一次休息时间是10时,故(2)正确;
11时到12时,小李骑了25﹣20=5(千米),故(3)正确;
返回时,小李的平均车速是30÷(16﹣14)=15(千米/小时),故(4)错误;
故答案为:(1)(2)(3).
三.解答题
16.解:(1)由x,y成一次函数关系可设y=kx+b,
将(0,100),(1,80)代入上式得:
,解得,
则它们之间的函数表达式为:y=﹣20x+100;
(2)当x=4.2时,由y=﹣20×4.2+100=16,
即汽车行驶4.2小时后,油箱内余油16升.
17.解:(1)根据题意,可得:y1=250+40×0.75x=30x+250;y2=40+40×0.95(x﹣1)=38x+2.
(2)令y1=y2,可得:30x+250=38x+2,
解方程,得x=31,
故答案为31.
18.解:(1)设每只A型口罩销售利润为a元,每只B型口罩销售利润为b元,根据题意得:
,
解得,
答:每只A型口罩销售利润为0.15元,每只B型口罩销售利润为0.2元;
(2)①根据题意得,y=0.15x+0.2(2000﹣x),即y=﹣0.05x+400;
根据题意得,,解得500≤x≤1000,
∴y=﹣0.05x+400(500≤x≤1000);
②∵y=﹣0.05x+400,k=﹣0.05<0;
∴y随x的增大而减小,
∵x为正整数,
∴当x=500时,y取最大值,则2000﹣x=1500,
即药店购进A型口罩500只、B型口罩1500只,才能使销售总利润最大.
同步练习
一.选择题
1.如图,一长为5m,宽为2m的长方形木板,现要在长边上截去长为xm的一部分,则剩余木板的面积(空白部分)y(m2)与x(m)的函数关系式为(0≤x<5)( )
A.y=10﹣x
B.y=5x
C.y=2x
D.y=﹣2x+10
2.某公司市场营销部的个人收入y(元)与其每月的销售量x(万件)成一次函数关系,其图象如图所示,营销人员没有销售量时最低收入是( )
A.1000
B.2000
C.3000
D.4000
3.A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.下列说法错误的是( )
A.乙晚出发1小时
B.乙出发3小时后追上甲
C.甲的速度是4千米/小时
D.乙先到达B地
4.设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回,设x秒后两车间的距离为y米,y关于x的函数关系如图所示,则甲车的速度为( )
A.10米/秒
B.11米/秒
C.12米/秒
D.13米/秒
5.小明用刻度不超过100℃的温度计来估计某食用油的沸点温度:将该食用油倒入锅中,均匀加热,每隔10s测量一次锅中的油温,得到如下数据:
时间t(单位:S)
0
10
20
30
40
油温y(单位:℃)
10
30
50
70
90
当加热100s时,油沸腾了,则小明估计这种油的沸点温度是( )
A.150℃
B.170℃
C.190℃
D.210℃
6.小红从家出发去晨跑,她离家的距离y(米)与时间x(分)的关系图象如图所示.下列结论错误的是( )
A.出发10分钟时,小红距离家1000米
B.整个晨跑过程一共走了3600米
C.返回时速度为60米/分
D.去时的平均速度小于返回速度
7.如图,甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离为S(km)和行驶时间t(h)之间的函数关系的图象如图所示,则下列结论错误的是( )
A.A、B两地相距18km
B.甲在途中停留了0.5小时
C.全程行驶时间乙比甲少用了1小时
D.乙出发后0.5小时追上甲
8.A、B两地相距90km,甲、乙两人从两地出发相向而行,甲先出发.图中l1.l2表示两人离A地的距离s(km)与时间t(h)的关系,结合图象,下列结论错误的是( )
A.l1是表示甲离A地的距离与时间关系的图象
B.乙的速度是30km/h
C.两人相遇时间在t=1.2h
D.当甲到达终点时乙距离终点还有45km
9.甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为xkg,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元.y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/kg
C.乙园超过5kg后,超过的部分价格优惠是打五折
D.若顾客采摘12kg草莓,那么到甲园或乙园的总费用相同
10.某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10﹣3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示.如果每毫升血液中含药量为5微克或5微克以上,对于治疗疾病是有效的,那么该药治疗的有效时间长是( )小时.
A.6
B.3
C.
D.
二.填空题
11.某高速列车公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,已知行李质量为30kg时,需付行李费4元;行李质量为40kg时,需付行李费12元,则旅客最多可免费携带
kg行李.
12.一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为
L.
13.甲、乙两地之间相距960千米,小新开车从甲地出发前往乙地,小白骑车从乙地出发前往甲地,已知小新比小白先出发1小时,两者均匀速行驶,当小新到达乙地后立即原路原速返回,在返回途中再次与小白相遇后两者都停止,如图是小新、小白两人之间的距离y(千米)与小新出发的时间x(小时)之间的图象,则当小新与小白第二次相遇时,小白离乙地的距离
千米.
14.甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,下列结论:
①甲、乙两地相距1800千米;
②点B的实际意义是两车出发后4小时相遇;
③动车的速度是280千米/小时;
④m=6,n=900.
其中正确的是
.(写出所有正确结论的序号)
15.周末,小李8时骑自行车从家里出发,到野外郊游,16时回到家里.他离家的距离S(千米)与时间t(时)之间的函数关系可以用图中的折线表示.现有如下信息:
(1)小李到达离家最远的地方的时间是14时;
(2)小李第一次休息时间是10时;
(3)11时到12时,小李骑了5千米;
(4)返回时,小李的平均车速是10千米/时.
其中,正确的信息有
(填序号).
三.解答题
16.一辆汽车在公路上匀速行驶,下表记录的是汽车在加满油后油箱内剩余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x(时)
0
1
2
剩余油量y(升)
100
80
60
(1)小明分析上表中所给的数据发现x,y成一次函数关系,试求出它们之间的函数表达式(不要求写出自变量的取值范围);
(2)求汽车行驶4.2小时后,油箱内剩余油多少升?
17.某社区的游泳馆按照顾客游泳的次数收取费用,每次的全票价为40元.在盛夏即将来临时,为吸引更多的顾客再次光顾,推出了以下两种收费方式.
方式一:先交250元会员费,每次游泳按照全票价的7.5折收取费用;
方式二:第一次收全票价,以后每次按照全票价的9.5折收取费用.
(1)按照方式一的总费用为y1,按照方式二的总费用为y2,请直接写出y1,y2与游泳次数x的函数关系式;
(2)去该游泳馆的次数等于
次时,两种方式收取总费用一样.
18.在近期“抗疫”期间,某药店销售A、B两种型号的口罩,已知销售80只A型和45只B型的利润为21元,销售40只A型和60只B型的利润为18元.
(1)求每只A型口罩和B型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不少于A型口罩的进货量且不超过它的3倍,设购进A型口罩x只,这2000只口罩的销售总利润为y元.
①求y关于x的函数关系式,并求出自变量x的取值范围;
②该药店购进A型、B型口罩各多少只,才能使销售总利润最大?
参考答案
一.选择题
1.解:由题意可得:y=2(5﹣x)
=10﹣2x.
故选:D.
2.解:设y与x的函数关系为y=kx+b,由题意得:
,
解得:,
∴y=5000x+2000,
当x=0时,
y=5000×0+2000=2000,
∴营销人员没有销售量时最低收入是2000元,
故选:B.
3.解:由图象可得,
乙晚出发1小时,故选项A正确;
乙出发3﹣1=2小时追上甲,故选项B错误;
甲的速度是12÷3=4(千米/小时),故选项C正确;
乙先到达B地,故选项D正确;
故选:B.
4.解:设甲车的速度为v1m/s,乙车的速度为v2m/s,
由图象可知:
开始时,乙车与甲车相距300米,
乙车用100秒追上了甲车,
∴100v1+300=100v2,
装完货物后,甲乙两车行驶了20秒后,两车相距500米,
∴20v1+20v2=500,
∴,
解得:,
故选:B.
5.解:设y=kt+b,
根据题意,得:,
解得,
∴y=2t+10,
当t=100时,y=2×100+10=210,
即当加热100s时,油沸腾了,小明估计这种油的沸点温度是210℃,
故选:D.
6.解:由图象可得:
x=10时y=1000,即出发10分钟时,小红距离家1000米,故本选项不合题意;
B.整个晨跑过程一共走了1800×2=3600(米),故本选项不合题意;
C.返回时速度为:1800÷(30﹣20)=180(米/分),故本选项符合题意;
D.去时的平均速度为:1800÷20=90(米/分),即去时的平均速度小于返回速度,故本选项不合题意.
故选:C.
7.解:A.由图可得,s为18千米,即A、B两地的距离是18千米,故A选项不合题意;
B.甲在0.5小时至1小时之间,S没有变化,说明甲在途中停留了0.5小时,故B选项不合题意;
C.由图可得,甲行驶的时间为2小时,乙行驶的时间为1.5小时,所以全程乙比甲少用了0.5小时,故C选项符合题意;
D.图中P点的实际意义是:甲,乙相遇,此时乙出发了0.5小时,故D选项不合题意.
故选:C.
8.解:∵甲先出发,
∴表示甲离A地的距离与时间关系的图象是l1,
故选项A不合题意;
乙的速度是:90÷(3.5﹣0.5)=90÷3=30(km/h),
故选项B不合题意;
设甲对应的函数解析式为y=ax+b,
,解得,
∴甲对应的函数解析式为y=﹣45x+90,
设乙对应的函数解析式为y=cx+d,
,解得,
即乙对应的函数解析式为y=30x﹣15,
,解得,
即甲出发1.4小时后两人相遇.
故选项C符合题意;
90﹣30×(2﹣0.5)=45(km),
即当甲到达终点时乙距离终点还有45km.
故选项D不符合题意.
故选:C.
9.解:由图象可得,
甲园的门票为60元,故选项A正确;
乙园草莓优惠前的销售价格是:200÷5=40(元/千克),故选项B正确;
=0.5,
即乙园超过5kg后,超过的部分价格优惠是打5折,故选项C正确;
若顾客采摘12kg草莓,甲园花费为:60+12×40×0.6=344(元),乙园的花费为:40×5+(12﹣5)×40×0.5=340(元),
∵344>340,
∴若顾客采摘12kg草莓,那么到甲园比到乙园的总费用高,故选项D错误;
故选:D.
10.解:当x≤2时,设y=k1x,
把(2,6)代入上式,得k1=3,
∴x≤2时,y=3x;
当x>2时,设y=k2x+b,把(2,6),(10,3)代入上式,
,解得,
∴y=;
把y=5代入y=3x,得x1=;
把y=5代入y=,得x2=,
则x2﹣x1=3小时.
即该药治疗的有效时间长是3小时.
故选:B.
二.填空题
11.解:设行李费y(元)与行李质量x(kg)的函数关系式为y=kx+b,
∵行李质量为30kg时,需付行李费4元;行李质量为40kg时,需付行李费12元,
∴,
解得,
即行李费y(元)与行李质量x(kg)的函数关系式为y=0.8x﹣20,
当y=0时,0=0.8x﹣20,解得x=25,
故答案为:25.
12.解:由图象可得,
每分钟的进水量为:20÷4=5(L),
每分钟的出水量为:5﹣(30﹣20)÷(12﹣4)=5﹣10÷8=5﹣1.25=3.75(L),
故答案为:3.75.
13.解:设小新的速度为akm/h,小白的速度为bkm/h,
根据题意得:,
解得,,
设第二次小新追上小白的时间为m小时,
120m﹣20(m﹣1)=960,
解得,m=9.4,
∴当小新与小白第二次相遇时,小白离乙地地的距离为:20×(9.4﹣1)=168(千米).
故答案为:168.
14.解:由图象可知,甲、乙两地相距1800千米,故①说法正确;
点B的实际意义是两车出发后4小时相遇,故②说法正确;
动车的速度为:1800÷4﹣150=300(km/h),故③说法错误;
150×4÷300+4=6,
∴m=6,n=150×6=900,
故④说法正确;
∴正确的是①②④.
故答案为:①②④.
15.解:由图象可得,
小李到达离家最远的地方的时间是14时,故(1)正确;
小李第一次休息时间是10时,故(2)正确;
11时到12时,小李骑了25﹣20=5(千米),故(3)正确;
返回时,小李的平均车速是30÷(16﹣14)=15(千米/小时),故(4)错误;
故答案为:(1)(2)(3).
三.解答题
16.解:(1)由x,y成一次函数关系可设y=kx+b,
将(0,100),(1,80)代入上式得:
,解得,
则它们之间的函数表达式为:y=﹣20x+100;
(2)当x=4.2时,由y=﹣20×4.2+100=16,
即汽车行驶4.2小时后,油箱内余油16升.
17.解:(1)根据题意,可得:y1=250+40×0.75x=30x+250;y2=40+40×0.95(x﹣1)=38x+2.
(2)令y1=y2,可得:30x+250=38x+2,
解方程,得x=31,
故答案为31.
18.解:(1)设每只A型口罩销售利润为a元,每只B型口罩销售利润为b元,根据题意得:
,
解得,
答:每只A型口罩销售利润为0.15元,每只B型口罩销售利润为0.2元;
(2)①根据题意得,y=0.15x+0.2(2000﹣x),即y=﹣0.05x+400;
根据题意得,,解得500≤x≤1000,
∴y=﹣0.05x+400(500≤x≤1000);
②∵y=﹣0.05x+400,k=﹣0.05<0;
∴y随x的增大而减小,
∵x为正整数,
∴当x=500时,y取最大值,则2000﹣x=1500,
即药店购进A型口罩500只、B型口罩1500只,才能使销售总利润最大.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
