沪教版(上海)初中数学九年级第一学期 本章小结 二次函数复习 教案
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 本章小结 二次函数复习 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 129.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 08:37:03 | ||
图片预览

文档简介
课题:二次函数复习
教学目标:
1、梳理二次函数的概念、图像特征与图像平移规律,巩固待定系数法确定二次函数的解析式,能用二次函数的知识解决一些综合问题;
2、在二次函数图像特征与图像平移规律运用等过程中,进一步体会函数思想、分类讨论思想、数形结合思想;体会解决问题方法的选择,提高分析问题和解决问题的能力
.
教学重难点:
重点:二次函数解析式的确定及其图像特征
难点:图像特征、与图形几何性质的综合运用.
教学过程:
(一)问题引领,梳理探索
问题1
观察下列y关于x的函数:
①y=3x-1
②y=3x2
③y=2(x+1)(x-1)
④y=x2-x(1+x)
⑤y=ax2+3x+1
⑥
其中一定是二次函数的有
(填序号)
.
追问:是二次函数吗?
【设计意图:复习二次函数的概念.】
问题2
已知抛物线
(1)抛物线的开口方向
,对称轴是
;
(2)抛物线的顶点坐标是____________,是最
点(填“高”或“低”);
(3)抛物线上有两点(2,y1)和(3,y2),则y1
y2(填“>”“=”“<”);
(4)将该抛物线向左平移3个单位,再向下平移1个单位所得新抛物线的表达式
是
问题3:(1)如果点A(2,m)在抛物线上,将此抛物线向右平移3个单位后,点A同时平移到点A’
,那么点A’坐标为_________.
(将上题中的“向右”改为“向上”这时点A’坐标为_________.)
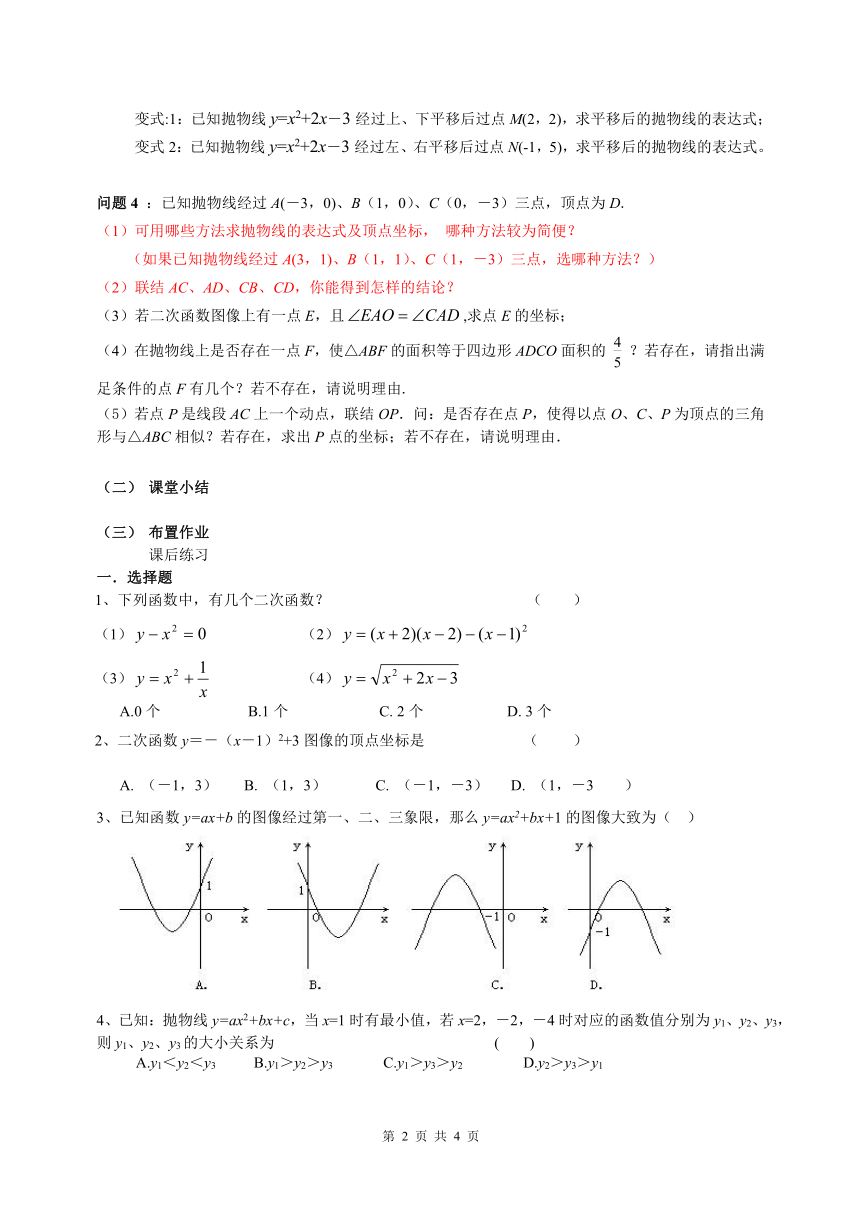
变式:1:已知抛物线y=x2+2x-3经过上、下平移后过点M(2,2),求平移后的抛物线的表达式;
变式2:已知抛物线y=x2+2x-3经过左、右平移后过点N(-1,5),求平移后的抛物线的表达式。
问题4
:已知抛物线经过A(-3,0)、B(1,0)、C(0,-3)三点,顶点为D.
可用哪些方法求抛物线的表达式及顶点坐标,
哪种方法较为简便?
(如果已知抛物线经过A(3,1)、B(1,1)、C(1,-3)三点,选哪种方法?)
联结AC、AD、CB、CD,你能得到怎样的结论?
(3)若二次函数图像上有一点E,且,求点E的坐标;
(4)在抛物线上是否存在一点F,使△ABF的面积等于四边形ADCO面积的
?若存在,请指出满足条件的点F有几个?若不存在,请说明理由.
(5)若点P是线段AC上一个动点,联结OP.问:是否存在点P,使得以点O、C、P为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.
课堂小结
布置作业
课后练习
一.选择题
1、下列函数中,有几个二次函数?
(
)
(1)
(2)
(3)
(4)
A.0个?????
B.1个
C.
2个
D.
3个
2、二次函数y=-(x-1)2+3图像的顶点坐标是
(?
)
A.
(-1,3)?????
B.
(1,3)???
C.
(-1,-3)??
D.
(1,-3)
3、已知函数y=ax+b的图像经过第一、二、三象限,那么y=ax2+bx+1的图像大致为(
)
4、已知:抛物线y=ax2+bx+c,当x=1时有最小值,若x=2,-2,-4时对应的函数值分别为y1、y2、y3,则y1、y2、y3的大小关系为
(
)
A.y1<y2<y3
B.y1>y2>y3
C.y1>y3>y2
D.y2>y3>y1
二.填空题
5、抛物线的顶点坐标是
.
6、抛物线的开口
,对称轴是
,顶点坐标是
,它可以看作是由抛物线向
平移
个单位得到的.
7、将抛物线y=x2向右平移4个单位后,再向上平移2个单位,则此时抛物线的解析式是
.
8、抛物线y=3x2可以看成由抛物线y=3(x﹣2)2+5向____平移___个单位,再向
平移
个单位所得.
9、抛物线y=2x2+4x+5的对称轴是
.
10、抛物线在对称轴
侧部分上升.
11、如图,抛物线,请判断下列各式的符号:
a
0;
b
0;
c
0.
12、已知二次函数的图像开口向上,且顶点在y轴的负半轴上,
请你写出一个满足条件的二次函数的表达式
.
13、如图所示的抛物线是二次函数的图像,那么的值是
.
14、如果抛物线经过点A(0,4)、B(2,m),那么m的值是
.
15、已知二次函数图像的对称轴在轴的左侧,且在对称轴的右侧函数的值随的增大而减小.请写出一个符合上述条件的二次函数的解析式
.(只需写一个)
16、二次函数的变量与变量部分对应值如下表:
…
…
…
…
那么时,对应的函数值
▲
.
三.解答题
17.已知二次函数的图像经过一次函数y=-x-4的图像与x轴、y轴的交点A、C,并且经过点
B(2,-
4),求这个二次函数的解析式;
18、已知二次函数的图像经过A(-3,0)、B(1,0)、C(0,-3)三点.
(1)求这个二次函数的解析式;
(2)若抛物线的顶点为D,求∠CAD与∠OBC的和;
(3)在轴上方的抛物线上是否存在一点M,过M作MN⊥轴于点N,使以A、M、N为顶点的三角形与△OBC相似?若存在,则求出点M的坐标;若不存在,请说明理由.
19、如图,二次函数图像的顶点为坐标原点O、且经过点A(3,3),一次函数的图像经过点A和点B(6,0).
(1)求二次函数与一次函数的解析式;
(2)如果一次函数图像与相交于点C,点D在线段AC上,与y轴平行的直线DE与二次函数图像相交于点E,∠CDO=∠OED,求点D的坐标.
第
4
页
共
4
页
教学目标:
1、梳理二次函数的概念、图像特征与图像平移规律,巩固待定系数法确定二次函数的解析式,能用二次函数的知识解决一些综合问题;
2、在二次函数图像特征与图像平移规律运用等过程中,进一步体会函数思想、分类讨论思想、数形结合思想;体会解决问题方法的选择,提高分析问题和解决问题的能力
.
教学重难点:
重点:二次函数解析式的确定及其图像特征
难点:图像特征、与图形几何性质的综合运用.
教学过程:
(一)问题引领,梳理探索
问题1
观察下列y关于x的函数:
①y=3x-1
②y=3x2
③y=2(x+1)(x-1)
④y=x2-x(1+x)
⑤y=ax2+3x+1
⑥
其中一定是二次函数的有
(填序号)
.
追问:是二次函数吗?
【设计意图:复习二次函数的概念.】
问题2
已知抛物线
(1)抛物线的开口方向
,对称轴是
;
(2)抛物线的顶点坐标是____________,是最
点(填“高”或“低”);
(3)抛物线上有两点(2,y1)和(3,y2),则y1
y2(填“>”“=”“<”);
(4)将该抛物线向左平移3个单位,再向下平移1个单位所得新抛物线的表达式
是
问题3:(1)如果点A(2,m)在抛物线上,将此抛物线向右平移3个单位后,点A同时平移到点A’
,那么点A’坐标为_________.
(将上题中的“向右”改为“向上”这时点A’坐标为_________.)
变式:1:已知抛物线y=x2+2x-3经过上、下平移后过点M(2,2),求平移后的抛物线的表达式;
变式2:已知抛物线y=x2+2x-3经过左、右平移后过点N(-1,5),求平移后的抛物线的表达式。
问题4
:已知抛物线经过A(-3,0)、B(1,0)、C(0,-3)三点,顶点为D.
可用哪些方法求抛物线的表达式及顶点坐标,
哪种方法较为简便?
(如果已知抛物线经过A(3,1)、B(1,1)、C(1,-3)三点,选哪种方法?)
联结AC、AD、CB、CD,你能得到怎样的结论?
(3)若二次函数图像上有一点E,且,求点E的坐标;
(4)在抛物线上是否存在一点F,使△ABF的面积等于四边形ADCO面积的
?若存在,请指出满足条件的点F有几个?若不存在,请说明理由.
(5)若点P是线段AC上一个动点,联结OP.问:是否存在点P,使得以点O、C、P为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.
课堂小结
布置作业
课后练习
一.选择题
1、下列函数中,有几个二次函数?
(
)
(1)
(2)
(3)
(4)
A.0个?????
B.1个
C.
2个
D.
3个
2、二次函数y=-(x-1)2+3图像的顶点坐标是
(?
)
A.
(-1,3)?????
B.
(1,3)???
C.
(-1,-3)??
D.
(1,-3)
3、已知函数y=ax+b的图像经过第一、二、三象限,那么y=ax2+bx+1的图像大致为(
)
4、已知:抛物线y=ax2+bx+c,当x=1时有最小值,若x=2,-2,-4时对应的函数值分别为y1、y2、y3,则y1、y2、y3的大小关系为
(
)
A.y1<y2<y3
B.y1>y2>y3
C.y1>y3>y2
D.y2>y3>y1
二.填空题
5、抛物线的顶点坐标是
.
6、抛物线的开口
,对称轴是
,顶点坐标是
,它可以看作是由抛物线向
平移
个单位得到的.
7、将抛物线y=x2向右平移4个单位后,再向上平移2个单位,则此时抛物线的解析式是
.
8、抛物线y=3x2可以看成由抛物线y=3(x﹣2)2+5向____平移___个单位,再向
平移
个单位所得.
9、抛物线y=2x2+4x+5的对称轴是
.
10、抛物线在对称轴
侧部分上升.
11、如图,抛物线,请判断下列各式的符号:
a
0;
b
0;
c
0.
12、已知二次函数的图像开口向上,且顶点在y轴的负半轴上,
请你写出一个满足条件的二次函数的表达式
.
13、如图所示的抛物线是二次函数的图像,那么的值是
.
14、如果抛物线经过点A(0,4)、B(2,m),那么m的值是
.
15、已知二次函数图像的对称轴在轴的左侧,且在对称轴的右侧函数的值随的增大而减小.请写出一个符合上述条件的二次函数的解析式
.(只需写一个)
16、二次函数的变量与变量部分对应值如下表:
…
…
…
…
那么时,对应的函数值
▲
.
三.解答题
17.已知二次函数的图像经过一次函数y=-x-4的图像与x轴、y轴的交点A、C,并且经过点
B(2,-
4),求这个二次函数的解析式;
18、已知二次函数的图像经过A(-3,0)、B(1,0)、C(0,-3)三点.
(1)求这个二次函数的解析式;
(2)若抛物线的顶点为D,求∠CAD与∠OBC的和;
(3)在轴上方的抛物线上是否存在一点M,过M作MN⊥轴于点N,使以A、M、N为顶点的三角形与△OBC相似?若存在,则求出点M的坐标;若不存在,请说明理由.
19、如图,二次函数图像的顶点为坐标原点O、且经过点A(3,3),一次函数的图像经过点A和点B(6,0).
(1)求二次函数与一次函数的解析式;
(2)如果一次函数图像与相交于点C,点D在线段AC上,与y轴平行的直线DE与二次函数图像相交于点E,∠CDO=∠OED,求点D的坐标.
第
4
页
共
4
页
