华东师大版八年级上册数学学案:14.1.2直角三角形的判定
文档属性
| 名称 | 华东师大版八年级上册数学学案:14.1.2直角三角形的判定 |
|
|
| 格式 | zip | ||
| 文件大小 | 50.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 08:52:38 | ||
图片预览

文档简介
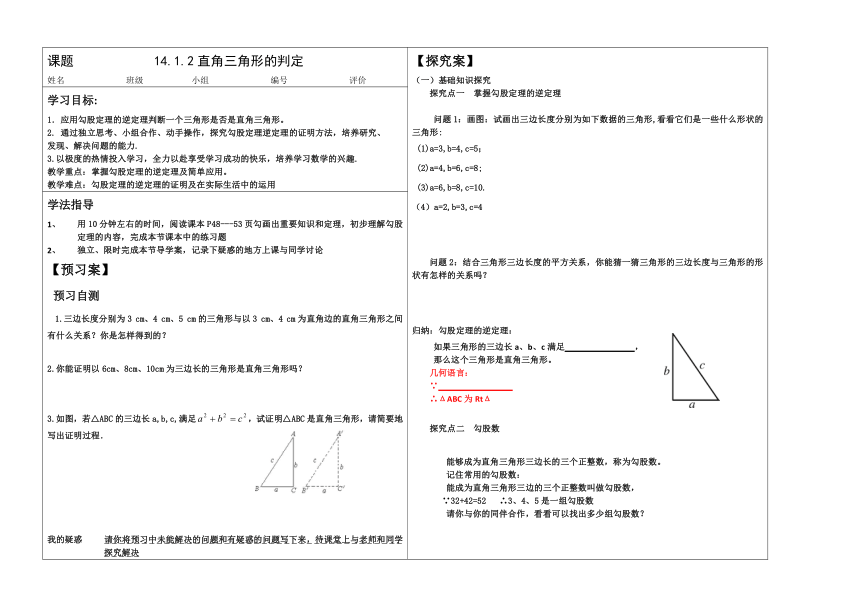
课题
14.1.2直角三角形的判定
姓名
班级
小组
编号
评价
【探究案】
(一)基础知识探究
探究点一
掌握勾股定理的逆定理
问题1:画图:试画出三边长度分别为如下数据的三角形,看看它们是一些什么形状的三角形:
(1)a=3,b=4,c=5;
(2)a=4,b=6,c=8;
(3)a=6,b=8,c=10.
(4)a=2,b=3,c=4
问题2:结合三角形三边长度的平方关系,你能猜一猜三角形的三边长度与三角形的形状有怎样的关系吗?
归纳:勾股定理的逆定理:
如果三角形的三边长a、b、c满足
,
那么这个三角形是直角三角形。
几何语言:
∵
∴ΔABC为RtΔ
探究点二
勾股数
能够成为直角三角形三边长的三个正整数,称为勾股数。
记住常用的勾股数:
能成为直角三角形三边的三个正整数叫做勾股数,
∵32+42=52
∴3、4、5是一组勾股数
请你与你的同伴合作,看看可以找出多少组勾股数?
变式训练
小明画了一个如图所示的四边形,其中AB=3,BC=12,CD=13,DA=4,∠A=90°,你能求出四边形ABCD的面积吗?
当堂检测
1、在△ABC中,三边长分别是8,15,17,则这个三角形是
,它的面积是
.
2、△ABC中,若a=5,b=12,则当c=
时,
∠C=90
3、三角形的两边为3和5,要使它成为直角三角形,则第三边长为
.
4、小蒋要求△ABC的的最长边上的高,测得AB=8cm,AC=6cm,BC=10cm。则可知最长边上的高_______
5.、满足下列条件的△ABC,不是直角三角形的是(
)
(A)a2
-
b2
=
c2
(B)a:b:c=3:4:5
(C)∠C=∠A-∠B
(D)
∠A:∠B
:
∠C
=3:4:5
6、在下列长度的各组线段中,能组成直角三角形的是(
)
A.
5,6,7
B.
32
,42
,52
C.
5,11,12
D.
5,12,13
7、我们知道3、4、5是一组勾股数,那么3k、4k、5k(k是正整数)也是一组勾股数吗?
我的收获:
学习目标:
1.应用勾股定理的逆定理判断一个三角形是否是直角三角形。
2.
通过独立思考、小组合作、动手操作,探究勾股定理逆定理的证明方法,培养研究、发现、解决问题的能力.
3.以极度的热情投入学习,全力以赴享受学习成功的快乐,培养学习数学的兴趣.
教学重点:掌握勾股定理的逆定理及简单应用。
教学难点:勾股定理的逆定理的证明及在实际生活中的运用
学法指导
用10分钟左右的时间,阅读课本P48---53页勾画出重要知识和定理,初步理解勾股定理的内容,完成本节课本中的练习题
独立、限时完成本节导学案,记录下疑惑的地方上课与同学讨论
【预习案】
预习自测
1.三边长度分别为3
cm、4
cm、5
cm的三角形与以3
cm、4
cm为直角边的直角三角形之间有什么关系?你是怎样得到的?
2.你能证明以6cm、8cm、10cm为三边长的三角形是直角三角形吗?
3.如图,若△ABC的三边长a,b,c,满足,试证明△ABC是直角三角形,请简要地写出证明过程.
我的疑惑
请你将预习中未能解决的问题和有疑惑的问题写下来,待课堂上与老师和同学探究解决
(二)知识综合应用探究
探究点一
勾股定理逆定理的应用(重点)
例1:设三角形三边长分别为下列各组数,试判断各三角形是否是直角三角形?
(1)7,24,25;
(2)12,35,37;
(3)13,11,9
拓展提升
判断由线段a、b、c
组成的三角形是不是直角三角形?如果是,指出哪一条边所对的角是直角.
(1)a=12,b=16,c=20
(2)
a=8,b=12,c=15
(3)
a=5,b=6,c=8
(4)
a:b:c=5:12:13
例2、一个零件的形状如下图所示,按照规定这个零件中∠A
和∠DBC都是直角.量得各边尺寸如图所示,这零件符合要求吗?并说明理由。
14.1.2直角三角形的判定
姓名
班级
小组
编号
评价
【探究案】
(一)基础知识探究
探究点一
掌握勾股定理的逆定理
问题1:画图:试画出三边长度分别为如下数据的三角形,看看它们是一些什么形状的三角形:
(1)a=3,b=4,c=5;
(2)a=4,b=6,c=8;
(3)a=6,b=8,c=10.
(4)a=2,b=3,c=4
问题2:结合三角形三边长度的平方关系,你能猜一猜三角形的三边长度与三角形的形状有怎样的关系吗?
归纳:勾股定理的逆定理:
如果三角形的三边长a、b、c满足
,
那么这个三角形是直角三角形。
几何语言:
∵
∴ΔABC为RtΔ
探究点二
勾股数
能够成为直角三角形三边长的三个正整数,称为勾股数。
记住常用的勾股数:
能成为直角三角形三边的三个正整数叫做勾股数,
∵32+42=52
∴3、4、5是一组勾股数
请你与你的同伴合作,看看可以找出多少组勾股数?
变式训练
小明画了一个如图所示的四边形,其中AB=3,BC=12,CD=13,DA=4,∠A=90°,你能求出四边形ABCD的面积吗?
当堂检测
1、在△ABC中,三边长分别是8,15,17,则这个三角形是
,它的面积是
.
2、△ABC中,若a=5,b=12,则当c=
时,
∠C=90
3、三角形的两边为3和5,要使它成为直角三角形,则第三边长为
.
4、小蒋要求△ABC的的最长边上的高,测得AB=8cm,AC=6cm,BC=10cm。则可知最长边上的高_______
5.、满足下列条件的△ABC,不是直角三角形的是(
)
(A)a2
-
b2
=
c2
(B)a:b:c=3:4:5
(C)∠C=∠A-∠B
(D)
∠A:∠B
:
∠C
=3:4:5
6、在下列长度的各组线段中,能组成直角三角形的是(
)
A.
5,6,7
B.
32
,42
,52
C.
5,11,12
D.
5,12,13
7、我们知道3、4、5是一组勾股数,那么3k、4k、5k(k是正整数)也是一组勾股数吗?
我的收获:
学习目标:
1.应用勾股定理的逆定理判断一个三角形是否是直角三角形。
2.
通过独立思考、小组合作、动手操作,探究勾股定理逆定理的证明方法,培养研究、发现、解决问题的能力.
3.以极度的热情投入学习,全力以赴享受学习成功的快乐,培养学习数学的兴趣.
教学重点:掌握勾股定理的逆定理及简单应用。
教学难点:勾股定理的逆定理的证明及在实际生活中的运用
学法指导
用10分钟左右的时间,阅读课本P48---53页勾画出重要知识和定理,初步理解勾股定理的内容,完成本节课本中的练习题
独立、限时完成本节导学案,记录下疑惑的地方上课与同学讨论
【预习案】
预习自测
1.三边长度分别为3
cm、4
cm、5
cm的三角形与以3
cm、4
cm为直角边的直角三角形之间有什么关系?你是怎样得到的?
2.你能证明以6cm、8cm、10cm为三边长的三角形是直角三角形吗?
3.如图,若△ABC的三边长a,b,c,满足,试证明△ABC是直角三角形,请简要地写出证明过程.
我的疑惑
请你将预习中未能解决的问题和有疑惑的问题写下来,待课堂上与老师和同学探究解决
(二)知识综合应用探究
探究点一
勾股定理逆定理的应用(重点)
例1:设三角形三边长分别为下列各组数,试判断各三角形是否是直角三角形?
(1)7,24,25;
(2)12,35,37;
(3)13,11,9
拓展提升
判断由线段a、b、c
组成的三角形是不是直角三角形?如果是,指出哪一条边所对的角是直角.
(1)a=12,b=16,c=20
(2)
a=8,b=12,c=15
(3)
a=5,b=6,c=8
(4)
a:b:c=5:12:13
例2、一个零件的形状如下图所示,按照规定这个零件中∠A
和∠DBC都是直角.量得各边尺寸如图所示,这零件符合要求吗?并说明理由。
