华东师大版八年级上册数学学案:14.2勾股定理的应用
文档属性
| 名称 | 华东师大版八年级上册数学学案:14.2勾股定理的应用 |
|
|
| 格式 | zip | ||
| 文件大小 | 53.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 08:56:31 | ||
图片预览

文档简介
课题
14.2
勾股定理的应用
姓名
班级
小组
编号
评价
【探究案】
探究点一
勾股定理在生活中的应用
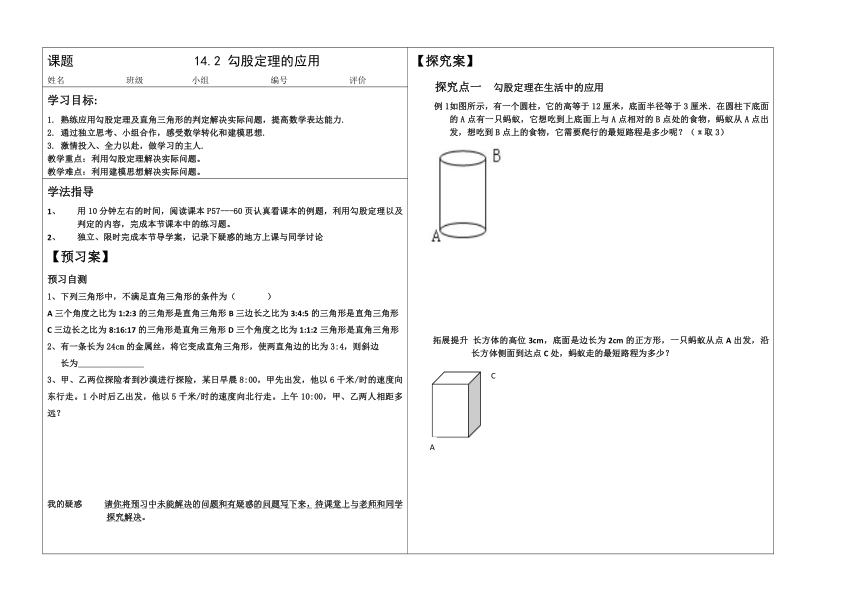
如图所示,有一个圆柱,它的高等于12厘米,底面半径等于3厘米.在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,蚂蚁从A点出发,想吃到B点上的食物,它需要爬行的最短路程是多少呢?(π取3)
拓展提升
长方体的高位3cm,底面是边长为2cm的正方形,一只蚂蚁从点A出发,沿长方体侧面到达点C处,蚂蚁走的最短路程为多少?
当堂检测
1、若一个三角形的三边长之比为5:12:13,且周长为60cm,则它的面积为
2、如图,阴影部分是以直角三角形的边长为边的正方形,根据图中数据,可求出阴影部分的面积为
3、如图,在一块平地上,张大爷家屋前9米处有一棵高约16米的大树,一次强风中这棵大树从离地面6米处折断倒下,大树倒下时能砸到张大爷的房子吗?理由是什么?
我的收获:
学习目标:
1.
熟练应用勾股定理及直角三角形的判定解决实际问题,提高数学表达能力.
2.
通过独立思考、小组合作,感受数学转化和建模思想.
3.
激情投入、全力以赴,做学习的主人.
教学重点:利用勾股定理解决实际问题。
教学难点:利用建模思想解决实际问题。
学法指导
用10分钟左右的时间,阅读课本P57---60页认真看课本的例题,利用勾股定理以及判定的内容,完成本节课本中的练习题。
独立、限时完成本节导学案,记录下疑惑的地方上课与同学讨论
【预习案】
预习自测
1、下列三角形中,不满足直角三角形的条件为(
)
A三个角度之比为1:2:3的三角形是直角三角形B三边长之比为3:4:5的三角形是直角三角形
C三边长之比为8:16:17的三角形是直角三角形D三个角度之比为1:1:2三角形是直角三角形
有一条长为24cm的金属丝,将它变成直角三角形,使两直角边的比为3:4,则斜边
长为
3、甲、乙两位探险者到沙漠进行探险,某日早晨8:00,甲先出发,他以6千米/时的速度向东行走。1小时后乙出发,他以5千米/时的速度向北行走。上午10:00,甲、乙两人相距多远?
我的疑惑
请你将预习中未能解决的问题和有疑惑的问题写下来,待课堂上与老师和同学探究解决。
例2
如右图长为10m的梯子AB斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么它的底端是否也滑动1m?
探究点二
勾股定理与等腰三角形的结合应用
例3
如图,在△ABC中,AB=26,BC=20,边BC上的中线AD=24.求AC的长.
例4如图,折叠长方形的一边AD,使点D落在BC边的点F
处,已知AB=8cm,BC=10cm,求CE的长。
14.2
勾股定理的应用
姓名
班级
小组
编号
评价
【探究案】
探究点一
勾股定理在生活中的应用
如图所示,有一个圆柱,它的高等于12厘米,底面半径等于3厘米.在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,蚂蚁从A点出发,想吃到B点上的食物,它需要爬行的最短路程是多少呢?(π取3)
拓展提升
长方体的高位3cm,底面是边长为2cm的正方形,一只蚂蚁从点A出发,沿长方体侧面到达点C处,蚂蚁走的最短路程为多少?
当堂检测
1、若一个三角形的三边长之比为5:12:13,且周长为60cm,则它的面积为
2、如图,阴影部分是以直角三角形的边长为边的正方形,根据图中数据,可求出阴影部分的面积为
3、如图,在一块平地上,张大爷家屋前9米处有一棵高约16米的大树,一次强风中这棵大树从离地面6米处折断倒下,大树倒下时能砸到张大爷的房子吗?理由是什么?
我的收获:
学习目标:
1.
熟练应用勾股定理及直角三角形的判定解决实际问题,提高数学表达能力.
2.
通过独立思考、小组合作,感受数学转化和建模思想.
3.
激情投入、全力以赴,做学习的主人.
教学重点:利用勾股定理解决实际问题。
教学难点:利用建模思想解决实际问题。
学法指导
用10分钟左右的时间,阅读课本P57---60页认真看课本的例题,利用勾股定理以及判定的内容,完成本节课本中的练习题。
独立、限时完成本节导学案,记录下疑惑的地方上课与同学讨论
【预习案】
预习自测
1、下列三角形中,不满足直角三角形的条件为(
)
A三个角度之比为1:2:3的三角形是直角三角形B三边长之比为3:4:5的三角形是直角三角形
C三边长之比为8:16:17的三角形是直角三角形D三个角度之比为1:1:2三角形是直角三角形
有一条长为24cm的金属丝,将它变成直角三角形,使两直角边的比为3:4,则斜边
长为
3、甲、乙两位探险者到沙漠进行探险,某日早晨8:00,甲先出发,他以6千米/时的速度向东行走。1小时后乙出发,他以5千米/时的速度向北行走。上午10:00,甲、乙两人相距多远?
我的疑惑
请你将预习中未能解决的问题和有疑惑的问题写下来,待课堂上与老师和同学探究解决。
例2
如右图长为10m的梯子AB斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么它的底端是否也滑动1m?
探究点二
勾股定理与等腰三角形的结合应用
例3
如图,在△ABC中,AB=26,BC=20,边BC上的中线AD=24.求AC的长.
例4如图,折叠长方形的一边AD,使点D落在BC边的点F
处,已知AB=8cm,BC=10cm,求CE的长。
