华东师大版八年级上册数学学案:第十四章勾股定理复习学案
文档属性
| 名称 | 华东师大版八年级上册数学学案:第十四章勾股定理复习学案 | 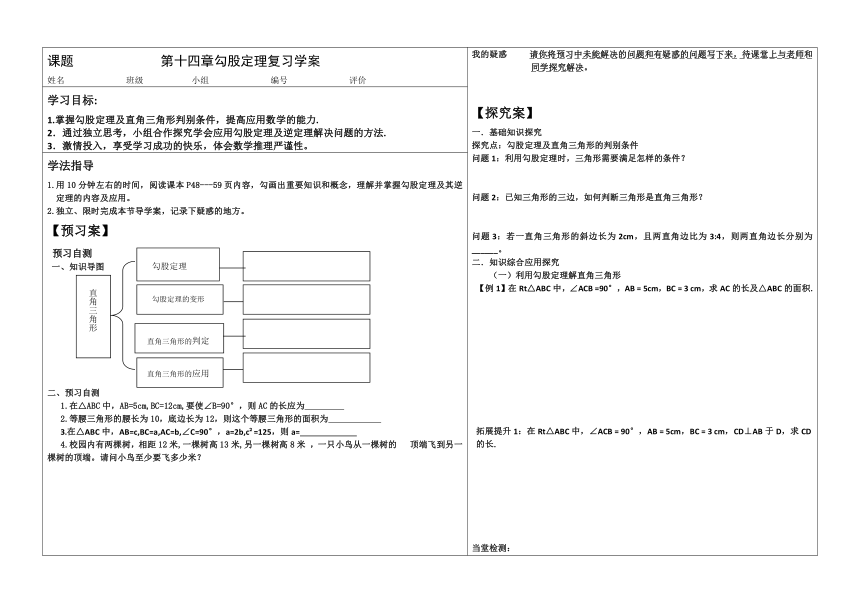 | |
| 格式 | zip | ||
| 文件大小 | 78.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 09:07:08 | ||
图片预览

文档简介
课题
第十四章勾股定理复习学案
姓名
班级
小组
编号
评价
我的疑惑
请你将预习中未能解决的问题和有疑惑的问题写下来,待课堂上与老师和同学探究解决。
【探究案】
一.基础知识探究
探究点:勾股定理及直角三角形的判别条件
问题1:利用勾股定理时,三角形需要满足怎样的条件?
问题2:已知三角形的三边,如何判断三角形是直角三角形?
问题3:若一直角三角形的斜边长为2cm,且两直角边比为3:4,则两直角边长分别为______。
二.知识综合应用探究
(一)利用勾股定理解直角三角形
【例1】在Rt△ABC中,∠ACB
=90°,AB
=
5cm,BC
=
3
cm,求AC的长及△ABC的面积.
拓展提升1:在Rt△ABC中,∠ACB
=
90°,AB
=
5cm,BC
=
3
cm,CD⊥AB于D,求CD的长.
当堂检测:
1.以下列各组线段为边构造三角形,其中能够得到直角三角形的是(
)
A.3,5,3
B.4,6,7
C.2,3,4
D.6,8,10
2.在△ABC中,已知AB=12,AC=9,BC=15,则△ABC的面积等于(
)
A.108
B.
54
C.180
D.
90
3.
如图所示,图中所有三角形是直角三角形,
所有四边形是正方有形,
,则=
.
4.如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体无盖盒子中,求细木棒露在盒外面的最短长度是多少?
我的收获:
学习目标:
1.掌握勾股定理及直角三角形判别条件,提高应用数学的能力.
2.通过独立思考,小组合作探究学会应用勾股定理及逆定理解决问题的方法.
3.激情投入,享受学习成功的快乐,体会数学推理严谨性。
学法指导
1.用10分钟左右的时间,阅读课本P48---59页内容,勾画出重要知识和概念,理解并掌握勾股定理及其逆定理的内容及应用。
2.独立、限时完成本节导学案,记录下疑惑的地方。
【预习案】
预习自测
一、知识导图
二、预习自测
1.在△ABC中,AB=5cm,BC=12cm,要使∠B=90°,则AC的长应为
2.等腰三角形的腰长为10,底边长为12,则这个等腰三角形的面积为
3.在△ABC中,AB=c,BC=a,AC=b,∠C=90°,a=2b,c?=125,则a=
4.校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米
,一只小鸟从一棵树的
顶端飞到另一棵树的顶端。请问小鸟至少要飞多少米?
拓展提升2.
在Rt△ABC中,三角形的三边分别为a.b.c,已知a=3,c=5,则b的长为多少?(易错题)
(二)勾股定理的逆定理的应用
【例2】如图已知D是?ABC边BC上一点,且AC?=AD?+DC?。小明说,由上面可得AC?-AB?=CD?-BD?,你说小明说得对吗?为什么?
拓展提升:
如图,在正方形ABCD中,E是AD的中点,点F在DC上且DF=DC,试判断BE与EF的位置关系,并说明理由。
第十四章勾股定理复习学案
姓名
班级
小组
编号
评价
我的疑惑
请你将预习中未能解决的问题和有疑惑的问题写下来,待课堂上与老师和同学探究解决。
【探究案】
一.基础知识探究
探究点:勾股定理及直角三角形的判别条件
问题1:利用勾股定理时,三角形需要满足怎样的条件?
问题2:已知三角形的三边,如何判断三角形是直角三角形?
问题3:若一直角三角形的斜边长为2cm,且两直角边比为3:4,则两直角边长分别为______。
二.知识综合应用探究
(一)利用勾股定理解直角三角形
【例1】在Rt△ABC中,∠ACB
=90°,AB
=
5cm,BC
=
3
cm,求AC的长及△ABC的面积.
拓展提升1:在Rt△ABC中,∠ACB
=
90°,AB
=
5cm,BC
=
3
cm,CD⊥AB于D,求CD的长.
当堂检测:
1.以下列各组线段为边构造三角形,其中能够得到直角三角形的是(
)
A.3,5,3
B.4,6,7
C.2,3,4
D.6,8,10
2.在△ABC中,已知AB=12,AC=9,BC=15,则△ABC的面积等于(
)
A.108
B.
54
C.180
D.
90
3.
如图所示,图中所有三角形是直角三角形,
所有四边形是正方有形,
,则=
.
4.如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体无盖盒子中,求细木棒露在盒外面的最短长度是多少?
我的收获:
学习目标:
1.掌握勾股定理及直角三角形判别条件,提高应用数学的能力.
2.通过独立思考,小组合作探究学会应用勾股定理及逆定理解决问题的方法.
3.激情投入,享受学习成功的快乐,体会数学推理严谨性。
学法指导
1.用10分钟左右的时间,阅读课本P48---59页内容,勾画出重要知识和概念,理解并掌握勾股定理及其逆定理的内容及应用。
2.独立、限时完成本节导学案,记录下疑惑的地方。
【预习案】
预习自测
一、知识导图
二、预习自测
1.在△ABC中,AB=5cm,BC=12cm,要使∠B=90°,则AC的长应为
2.等腰三角形的腰长为10,底边长为12,则这个等腰三角形的面积为
3.在△ABC中,AB=c,BC=a,AC=b,∠C=90°,a=2b,c?=125,则a=
4.校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米
,一只小鸟从一棵树的
顶端飞到另一棵树的顶端。请问小鸟至少要飞多少米?
拓展提升2.
在Rt△ABC中,三角形的三边分别为a.b.c,已知a=3,c=5,则b的长为多少?(易错题)
(二)勾股定理的逆定理的应用
【例2】如图已知D是?ABC边BC上一点,且AC?=AD?+DC?。小明说,由上面可得AC?-AB?=CD?-BD?,你说小明说得对吗?为什么?
拓展提升:
如图,在正方形ABCD中,E是AD的中点,点F在DC上且DF=DC,试判断BE与EF的位置关系,并说明理由。
