人教版数学九年级下册-26.1.2反比例函数的图象和性质-教案(表格式)
文档属性
| 名称 | 人教版数学九年级下册-26.1.2反比例函数的图象和性质-教案(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 136.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 11:10:12 | ||
图片预览

文档简介
教师姓名
单位名称
填写时间
2020.8.18
学科
数学
年级/册
九年级下册
教材版本
人教版
课题名称
第二十六章第一节第三课时
反比例函数比例系数k的几何意义
难点名称
灵活运用反比例函数比例系数k的几何意义
难点分析
从知识角度分析为什么难
学生已经具有了函数概念的知识积累,在上一节课的学习中,学生已经掌握了反比例函数的概念及其图象与性质。反比例函数的图象与几何图形往往结合紧密,如何识别图象中的信息来解决数学问题对初学反比例函数的九年级学生来说是一大难点。
从学生角度分析为什么难
以反比例函数为背景的图形面积题型问题在教材中没有系统呈现,但它的掌握又直接影响到后续知识的学习,在教辅资料、考题中比较常见,学生在解此类题型由于缺乏方法而感到困难。
难点教学方法
让学生自己尝试在
的图象上任取一点P(x,y),过P点分别向x、y轴作垂线,从而探究求出两垂线与坐标轴形成的矩形的面积及直角三角形的面积,从而探究所形成的矩形面积、直角三角形的面积与k的关系。
教学环节
教学过程
复习导入
一、复习引入
1.反比例函数的一般形式是什么?
2.如何确定比例系数k的值?
3.反比例函数中的比例系数k可以确定函数的什么?
比例系数k还有什么作用呢?
知识讲解
(难点突破)
二、探索新知
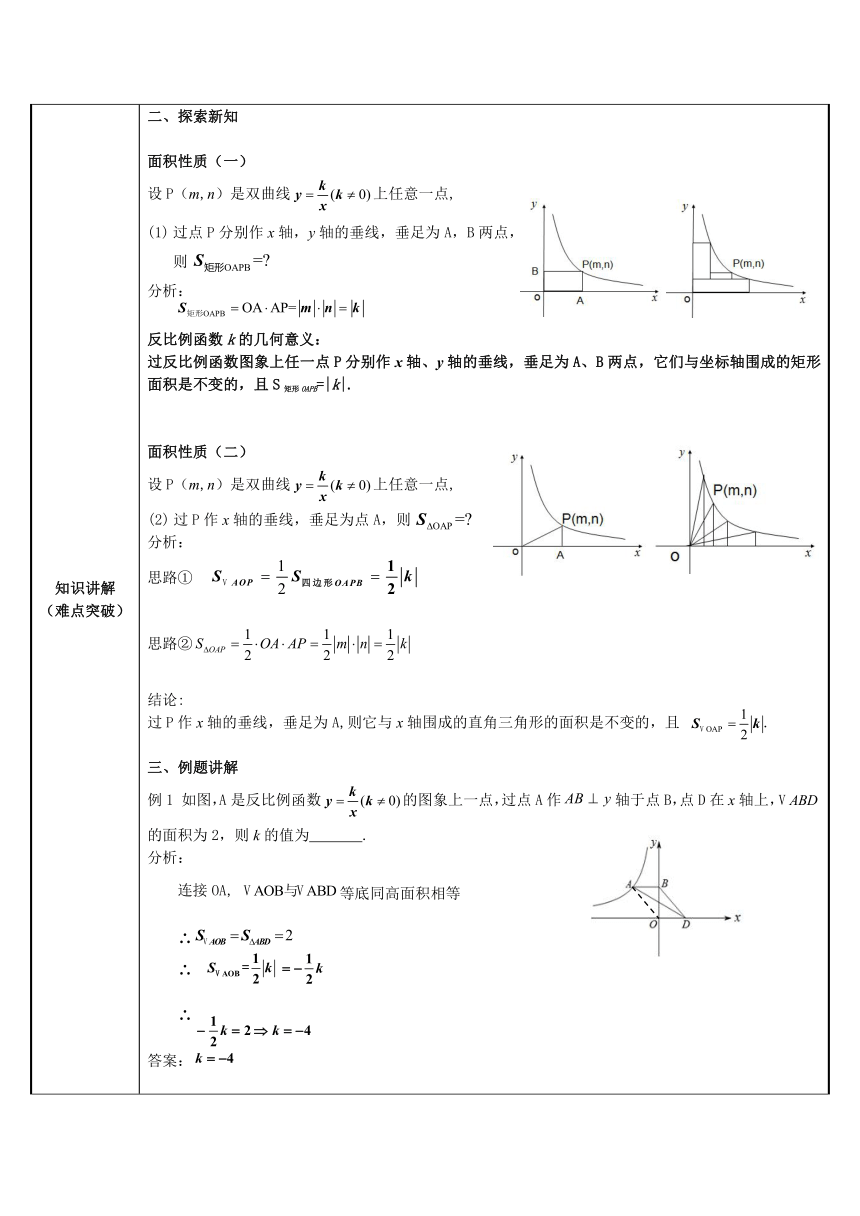
面积性质(一)
设P(m,n)是双曲线上任意一点,
过点P分别作x轴,y轴的垂线,垂足为A,B两点,
则
分析:
反比例函数k的几何意义:
过反比例函数图象上任一点P分别作x轴、y轴的垂线,垂足为A、B两点,它们与坐标轴围成的矩形面积是不变的,且S矩形OAPB=|k|.
面积性质(二)
设P(m,n)是双曲线上任意一点,
过P作x轴的垂线,垂足为点A,则
分析:
思路①
思路②
结论:
过P作x轴的垂线,垂足为A,则它与x轴围成的直角三角形的面积是不变的,且
.
三、例题讲解
例1
如图,A是反比例函数的图象上一点,过点A作
轴于点B,点D在x轴上,的面积为2,则k的值为???
.
分析:
连接OA,
等底同高面积相等
∴
∴
∴
答案:
结论:
过P作x轴或y轴的垂线,垂足为A,则它与坐标轴围成的直角三角形的面积是不变的,
且
.
例2.如图,点A在双曲线
上,点B在双曲线
上,
且AB∥
x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为???
.
分析:
过点A作轴于点E,则
,
∴
答案:1
归纳:
已知反比例函数比例系数k的值,可以求出函数图象上一点与坐标轴所围成的矩形或直角三角形的面积;
反之,已知它们的面积也可以求出反比例函数比例系数k的值,这也告诉了我们一种新的求k值的方法.
课堂练习
(难点巩固)
四、课堂练习
1.如图,A、C是函数
的图象上任意两点,过A作x轴的垂线,垂足为B;过C作y轴的垂线,垂足为D.记Rt△AOB的面积为S1,
Rt△OCD的面积为S2
,则S1与S
2大小关系为(
)
A.S1>S2
B.S1C.S1
=
S2
D.S1和S2的大小关系不能确定.
分析:
答案:选C
2.如图,已知点A在函数
的图象上,
轴于点B,OC=AB,则四边形OCBA的面积为???
.
分析:
由题意可知,四边形OCBA为平行四边形
∴
答案:3
五、拓展提高
如图,反比例函数
的图象经过矩形OABC
对角线的交点F,分
别与AB、BC
相交于点D、E.若四边形OEBD的面积为12,则k的值(
)
A.1
B.
2
C.
3
D.
4
分析:过F点分别作x、y轴的垂线,垂足依次为点N、M,
由题意可知,
∴4k=12+k,k=4
答案:选D
课堂小结
六、归纳小结
反比例函数中比例系数“k”的几何意义:
过反比例函数图象上任一点P分别作x轴、y轴的垂线,垂足为A、
B
两点,则它们与坐标轴围成的矩形面积
S矩形OAPB=|k|.
过P作x轴或y轴的垂线,垂足为A,则它与坐标轴围成的直角三角形的面积
.
3.体现解题思想:数形结合的思想、转化的思想.
单位名称
填写时间
2020.8.18
学科
数学
年级/册
九年级下册
教材版本
人教版
课题名称
第二十六章第一节第三课时
反比例函数比例系数k的几何意义
难点名称
灵活运用反比例函数比例系数k的几何意义
难点分析
从知识角度分析为什么难
学生已经具有了函数概念的知识积累,在上一节课的学习中,学生已经掌握了反比例函数的概念及其图象与性质。反比例函数的图象与几何图形往往结合紧密,如何识别图象中的信息来解决数学问题对初学反比例函数的九年级学生来说是一大难点。
从学生角度分析为什么难
以反比例函数为背景的图形面积题型问题在教材中没有系统呈现,但它的掌握又直接影响到后续知识的学习,在教辅资料、考题中比较常见,学生在解此类题型由于缺乏方法而感到困难。
难点教学方法
让学生自己尝试在
的图象上任取一点P(x,y),过P点分别向x、y轴作垂线,从而探究求出两垂线与坐标轴形成的矩形的面积及直角三角形的面积,从而探究所形成的矩形面积、直角三角形的面积与k的关系。
教学环节
教学过程
复习导入
一、复习引入
1.反比例函数的一般形式是什么?
2.如何确定比例系数k的值?
3.反比例函数中的比例系数k可以确定函数的什么?
比例系数k还有什么作用呢?
知识讲解
(难点突破)
二、探索新知
面积性质(一)
设P(m,n)是双曲线上任意一点,
过点P分别作x轴,y轴的垂线,垂足为A,B两点,
则
分析:
反比例函数k的几何意义:
过反比例函数图象上任一点P分别作x轴、y轴的垂线,垂足为A、B两点,它们与坐标轴围成的矩形面积是不变的,且S矩形OAPB=|k|.
面积性质(二)
设P(m,n)是双曲线上任意一点,
过P作x轴的垂线,垂足为点A,则
分析:
思路①
思路②
结论:
过P作x轴的垂线,垂足为A,则它与x轴围成的直角三角形的面积是不变的,且
.
三、例题讲解
例1
如图,A是反比例函数的图象上一点,过点A作
轴于点B,点D在x轴上,的面积为2,则k的值为???
.
分析:
连接OA,
等底同高面积相等
∴
∴
∴
答案:
结论:
过P作x轴或y轴的垂线,垂足为A,则它与坐标轴围成的直角三角形的面积是不变的,
且
.
例2.如图,点A在双曲线
上,点B在双曲线
上,
且AB∥
x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为???
.
分析:
过点A作轴于点E,则
,
∴
答案:1
归纳:
已知反比例函数比例系数k的值,可以求出函数图象上一点与坐标轴所围成的矩形或直角三角形的面积;
反之,已知它们的面积也可以求出反比例函数比例系数k的值,这也告诉了我们一种新的求k值的方法.
课堂练习
(难点巩固)
四、课堂练习
1.如图,A、C是函数
的图象上任意两点,过A作x轴的垂线,垂足为B;过C作y轴的垂线,垂足为D.记Rt△AOB的面积为S1,
Rt△OCD的面积为S2
,则S1与S
2大小关系为(
)
A.S1>S2
B.S1
=
S2
D.S1和S2的大小关系不能确定.
分析:
答案:选C
2.如图,已知点A在函数
的图象上,
轴于点B,OC=AB,则四边形OCBA的面积为???
.
分析:
由题意可知,四边形OCBA为平行四边形
∴
答案:3
五、拓展提高
如图,反比例函数
的图象经过矩形OABC
对角线的交点F,分
别与AB、BC
相交于点D、E.若四边形OEBD的面积为12,则k的值(
)
A.1
B.
2
C.
3
D.
4
分析:过F点分别作x、y轴的垂线,垂足依次为点N、M,
由题意可知,
∴4k=12+k,k=4
答案:选D
课堂小结
六、归纳小结
反比例函数中比例系数“k”的几何意义:
过反比例函数图象上任一点P分别作x轴、y轴的垂线,垂足为A、
B
两点,则它们与坐标轴围成的矩形面积
S矩形OAPB=|k|.
过P作x轴或y轴的垂线,垂足为A,则它与坐标轴围成的直角三角形的面积
.
3.体现解题思想:数形结合的思想、转化的思想.
