北师大版七年级上册第五章一元一次方程 单元测试卷(word版含答案)
文档属性
| 名称 | 北师大版七年级上册第五章一元一次方程 单元测试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 107.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 12:44:34 | ||
图片预览


文档简介
《一元一次方程》单元测试卷详解
一.选择题(每小题3分共36分)
1.下列是一元一次方程的是(
)
A.
B.
C.
D.
2.若方程是关于x的一元一次方程,则m的值是(
)
A.
2
B.
-2
C.
2或-2
D.
1或-1
3.如果x=5是关于x的方程的解,则m的值是(
)
A.
-40
B.
4
C.
-4
D.
-2
4.如果2(x+3)的值与3(1-x)的值互为相反数,那么x的值为(
)
A.
9
B.
8
C.
-9
D.
-8
5.点A在数轴上,点A所对应的数用2a+1表示,且点A到原点的距离等于3,则a的值为(
)
A.
-2或1
B.
-2或2
C.
-2
D.
1
6.今年哥哥的年龄是妹妹年龄的2倍,4年前哥哥的年龄是妹妹年龄的3倍,若设妹妹今年x岁,可列方程为(
)
A.
2x+4=3(x-4)
B.
2x-4=3(x-4)
C.
2x=3(x-4)
D.
2x-4=3x
7.如图,天秤中的物体a,b,c,则物体a与物体c的重量关系是(
)
A.
a=c
B.
a=2c
C.
2a=3c
D.
4a=9c
8.某中学七年级举行足球友谊赛,规定:胜一场记3分,平一场记1分,负1场记0分,七年级(1)班在第一轮比赛中共记8分,其中胜的场数与平的场数相同,负的场数比胜的场数多1场,则七年级(1)班在此轮比赛中共负(
)场
A.
3
B.
4
C.
5
D.
6
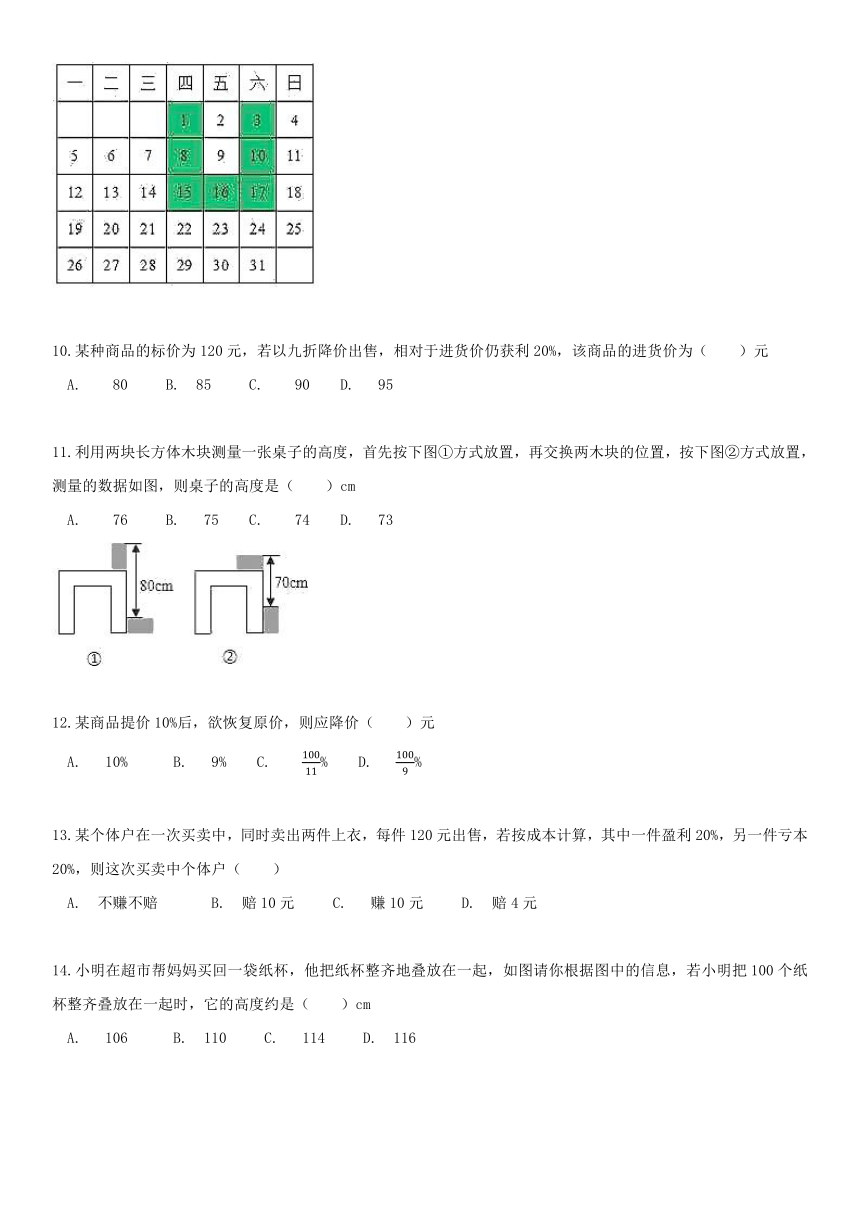
9.表中给出的是某月的月历,任意选取“U”形框中的7个数(如阴影部分),请你运用所学的数学知识来研究,发现这7个数的和不可能是(
)
A.
70
B.
78
C.
147
D.
105
10.某种商品的标价为120元,若以九折降价出售,相对于进货价仍获利20%,该商品的进货价为(
)元
A.
80
B.
85
C.
90
D.
95
11.利用两块长方体木块测量一张桌子的高度,首先按下图①方式放置,再交换两木块的位置,按下图②方式放置,测量的数据如图,则桌子的高度是(
)cm
A.
76
B.
75
C.
74
D.
73
12.某商品提价10%后,欲恢复原价,则应降价(
)元
A.
10%
B.
9%
C.
%
D.
%
13.某个体户在一次买卖中,同时卖出两件上衣,每件120元出售,若按成本计算,其中一件盈利20%,另一件亏本20%,则这次买卖中个体户(
)
A.
不赚不赔
B.
赔10元
C.
赚10元
D.
赔4元
14.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是(
)cm
A.
106
B.
110
C.
114
D.
116
15.如图,数轴上的点O和点A分别表示0和10,点P是线段OA上一动点,点P沿O---A---O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(t不超过10秒),若点P在运动过程中,当PB=2时,则运动时间t的值为(
)秒
A.
或
B.
或或
或
C.
或
D.
或或或
二.填空题(共5小题共15分)
16.把方程变形为x=2,其依据是________________
17.代数式2a+1与1-3a互为相反数,则a=_________
18.汽车运送一批货物,若每辆车装4吨,还剩下8吨未装;若每辆车装4.5吨,恰好装完,这个车队有_______辆车.
19.如图,一块长5cm,宽为2cm的长方形纸板,一块长为4cm,宽为1cm的长方形纸板与一块小正方形及两块长方形纸板,恰好拼成一个大正方形,则小正方形纸板的面积是_________
20.已知某铁路桥长600米,现有一列火车通过该桥,火车从开始上桥到过完桥共用了30秒钟,整列火车完全在桥上的时间为20秒,则火车长度为________米
三.解答题
21.(18分)解方程:
(1)
2x+3(5-x)=4
(2)
(3)
y+1=-y
(4)
(5)
4(x-3)-(3-x)=7(3-x)-(x-3)
(6)
22.(6分)
小明看一本故事书,第一天看了全书的,第二天看了剩下的一半,第三天看了60页刚好看完,这本故事书一共有多少页?
23.(6分)一个三位数和一个两位数的差为225,在三位数的左边写上这个两位数,得到一个五位数,在三位数的右边写上这个两位数,也得到一个五位数,已知前面的五位数比后面的五位数大225,求这个三位数和两位数.
24.(6分)某小区便利店到厂家购进A,B两种香油共140瓶,花了1000元,其中A香油的进价为6.5元/瓶,售价为8元/瓶;B香油的进价为8元/瓶,售价为10元/瓶;
(1)该店购进A,B两种香油各多少瓶?
(2)将购进的140瓶香油全部售完,可获利多少元?
25.(6分)解答下列问题:
(1)一项工作,甲独做需要18天,乙独做需要24天,若两人合做8天后,余下的工作再由甲独做多少天可完成?
(2)甲一天能加工A种零件50个或B种零件20个,1个A种零件与2个B种零件配成一套,那么甲30天时间安排多少天做A种零件,多少天做B种零件,才能使得所有零件都刚好配套?
解题详解
1.
解析:选项A:一元二次方程;选项B:二元一次方程;选项D:分式方程;,故选C
2.
解析:由题可得:m-2≠0,|m|-1=1,解得m-2,故选B
3.
解析:把x=5代入方程,可解得m=-4,故选C
4.
解析:由题可得2(x+3)+3(1-x)=0,解得x=9,故选A
5.
解析:由题可得:|2a+1|=3,解得a=-2或1,故选A
6.
解析:妹妹今年x岁,则哥哥今年2x岁,4年前妹妹(x-4)岁,哥哥(2x-4)岁,由“哥=妹×3”可列方程,故选B
7.
解析:由图可知:2a=3b,2b=3c,则4a=6b,6b=9c,∴4a=9c,故选D.
8.
解析:设负x场,则胜与平的场数都是(x-1)场,由题可得:3(x-1)+(x-1)=8,解得x=3,故选A
9.
解析:设“U”型框的正中间的数为x,则其他6个数分别为x-15、x-13、x-8、x-6、x-1、x+1,则7个数的和为7x-42;其中选项B:7x-42=78,解得x不是整数;故选项B.
10.
解析:设进货价为x元,由等量关系式“利润=进货价×利润率=标价×折扣-进货价”可列方程为:20%x=120×0.9-x,解得x=90,故选C
11.
解析:由图①可得等量关系式:桌高=80-长+宽…①;
由图②可得等量关系式:桌高=70-宽+长…②,
①+②可得:2桌高=70+80,∴桌高=75cm,故选B
12.
解析:假设原价为100元,则提价为110元,应降价(110-100)÷110=%,故选C
13.
解析:
设第一件上衣的成本为x元,由等量关系式“成本×(1+利润率)=售价“可列方程:
(1+20%)x=120,解得x=100;
设第二件上衣的成本为x元,由等量关系式“成本×(1-亏损率)=售价”可列方程:
(1-20%)x=120,解得x=150;
所以,这两件上衣的总成本为250元,总售价为240元,亏损了10元,故选B
14.
解析:由图可得等量关系式:“8个杯子高度-3个杯子高度=5个杯口叠放高度=14-9=5cm”,则可得每2个杯口叠放高度为1cm,由图1可得等量关系式为“1个杯高+3个杯口叠放高度=9cm”,则可得1个杯高为6cm。小明把100个杯子叠放,则等量关系式为:总高度=1个杯高+100个杯口叠放高度=6+100=106cm,故选A
15.
解析:由题可知B所表示的数为5,OB=AB=5,
(1)当P由O---A运动时,
①当P在B点左侧时,由题可知OP=2t,BP=5-2t,则5-2t=2,∴t=;
②当p在B点右侧时,由题可知OP=2t,BP=2t-5,则2t-5=2,∴t=;
(2)当P由A---O运动时,
③当P在B点右侧时,由题可知P点的路程为2t,AP=2t-10,BP=5-(2t-10)=2t+15,则2t+15=2,∴t=;
④当P在B点右侧时,由题可知P点的路程为2t,OP=20-2t,BP=5-(20-2t)=2t-15,则2t-15=2,∴t=;
综上所述,当PB=2时,则运动时间t的值为秒或秒或
秒或秒,故选B
16.
解析:依据是:等式性质二
17.
解析:由题意可得:2a+1+1-3a=0,解得a=2
18.
解析:设有x辆车,由题意可得:4x+8=4.5x,解得x=16,所以这个车队有16辆车
19.
解析:设小正方形的边长为x,则从上下看,大正方形的边长为x+1+2,从左右看,大正方形的边长为4+5-x,由此可列方程为:x+1+2=4+5-x,解得x=3,故小正方形的面积为9.
20.
解析:由条件“火车从开始上桥到过完桥共用了30秒钟”可得等量关系式“600+车长=30×火车速度”;由条件“整列火车完全在桥上的时间为20秒”可得等量关系式“600-车长=20×火车速度”;由火车速度相同可列方程为:,解是x=120,故火车长度为120米.
21.
解析:(1)解:
2x+15-3x=4,2x-3x=4-15,-x=-11,x=11
(2)解:3(x-1)-6=2(4x+1),3x-3-6=8x+2,3x-8x=2+3+6,-5x=11,x=
(3)解:5y+10=2(4y-2)-10y,5y+10=8y-4-10y,5y-8y+10y=-4-10,7y=-14,y=-2
(4)解:,3-x-12-2x=6,-x-2x=6-3+12,-3x=15,x=-5
(5)解:4(x-3)-(3-x)-7(3-x)+(x-3)=0,
4(x-3)+(x-3)+7(x-3)+(x-3)=0,(x-3)(4++7+)=0,∴x-3=0,x=3
(6)解:,70x-3(9-2x)=21,70x-27+6x=21,76x=48,x=
22.
解析:设这本故事书一共x页,则第二天看了全书的(1-)×=,由等量关系式“全书-第一天看的+第二天看的=剩下的60页”可列方程为:x-x-x=60,解得x=150,∴这本故事书一共有150页
23.
解析:设两位数为x,则三位数为x+225,在三位数的左边写上这个两位数所得到一个五位数可表示为:100a+a+225,在三位数的右边写上这个两位数所得到一个五位数可以表示为:100(a+225)+a,由等量关系式“第一个五位数-225=第二个五位数”可列方程为:100a+a+225-225=100(a+225)+a,解得a=25,则a+225=25+225=250,∴这个三位数为250,这个两位数为25
24.
解析:(1)设A种香油有x瓶,则B种香油有(140-x)瓶,由等量关系式“A的总价+B的总价=1000”可列方程为:6.5x+8(140-x)=1000,解得x=80,则140-x=140-80=60,∴该店购进A种香油有80瓶,则B种香油有60瓶;
(2)由等量关系式“总利润=A利润+B利润=A数量×每瓶利润+B数量×每瓶利润”列式为:
(8-6.5)×80+(10-8)×60=240(元),故全部售完可获利240元
25.
解析:(1)设甲独做x天可完成,由等量关系式“8×(甲的工作效率+乙工作效率)+2×甲的工作效率=1”可列方程为:,解得x=4,即余下的工作再由甲独做4天可完成
(2)设安排x天做A种零件,(30-x)天做B种零件,由等量关系式“A总零件:B总零件=1:2,即2×A总零件=B总零件”可列方程为:2×50x=20(30-x),解得x=5,则30-x=30-5=25,∴甲30天时间安排5天做A种零件,25天做B种零件,才能使得所有零件都刚好配套
一.选择题(每小题3分共36分)
1.下列是一元一次方程的是(
)
A.
B.
C.
D.
2.若方程是关于x的一元一次方程,则m的值是(
)
A.
2
B.
-2
C.
2或-2
D.
1或-1
3.如果x=5是关于x的方程的解,则m的值是(
)
A.
-40
B.
4
C.
-4
D.
-2
4.如果2(x+3)的值与3(1-x)的值互为相反数,那么x的值为(
)
A.
9
B.
8
C.
-9
D.
-8
5.点A在数轴上,点A所对应的数用2a+1表示,且点A到原点的距离等于3,则a的值为(
)
A.
-2或1
B.
-2或2
C.
-2
D.
1
6.今年哥哥的年龄是妹妹年龄的2倍,4年前哥哥的年龄是妹妹年龄的3倍,若设妹妹今年x岁,可列方程为(
)
A.
2x+4=3(x-4)
B.
2x-4=3(x-4)
C.
2x=3(x-4)
D.
2x-4=3x
7.如图,天秤中的物体a,b,c,则物体a与物体c的重量关系是(
)
A.
a=c
B.
a=2c
C.
2a=3c
D.
4a=9c
8.某中学七年级举行足球友谊赛,规定:胜一场记3分,平一场记1分,负1场记0分,七年级(1)班在第一轮比赛中共记8分,其中胜的场数与平的场数相同,负的场数比胜的场数多1场,则七年级(1)班在此轮比赛中共负(
)场
A.
3
B.
4
C.
5
D.
6
9.表中给出的是某月的月历,任意选取“U”形框中的7个数(如阴影部分),请你运用所学的数学知识来研究,发现这7个数的和不可能是(
)
A.
70
B.
78
C.
147
D.
105
10.某种商品的标价为120元,若以九折降价出售,相对于进货价仍获利20%,该商品的进货价为(
)元
A.
80
B.
85
C.
90
D.
95
11.利用两块长方体木块测量一张桌子的高度,首先按下图①方式放置,再交换两木块的位置,按下图②方式放置,测量的数据如图,则桌子的高度是(
)cm
A.
76
B.
75
C.
74
D.
73
12.某商品提价10%后,欲恢复原价,则应降价(
)元
A.
10%
B.
9%
C.
%
D.
%
13.某个体户在一次买卖中,同时卖出两件上衣,每件120元出售,若按成本计算,其中一件盈利20%,另一件亏本20%,则这次买卖中个体户(
)
A.
不赚不赔
B.
赔10元
C.
赚10元
D.
赔4元
14.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是(
)cm
A.
106
B.
110
C.
114
D.
116
15.如图,数轴上的点O和点A分别表示0和10,点P是线段OA上一动点,点P沿O---A---O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(t不超过10秒),若点P在运动过程中,当PB=2时,则运动时间t的值为(
)秒
A.
或
B.
或或
或
C.
或
D.
或或或
二.填空题(共5小题共15分)
16.把方程变形为x=2,其依据是________________
17.代数式2a+1与1-3a互为相反数,则a=_________
18.汽车运送一批货物,若每辆车装4吨,还剩下8吨未装;若每辆车装4.5吨,恰好装完,这个车队有_______辆车.
19.如图,一块长5cm,宽为2cm的长方形纸板,一块长为4cm,宽为1cm的长方形纸板与一块小正方形及两块长方形纸板,恰好拼成一个大正方形,则小正方形纸板的面积是_________
20.已知某铁路桥长600米,现有一列火车通过该桥,火车从开始上桥到过完桥共用了30秒钟,整列火车完全在桥上的时间为20秒,则火车长度为________米
三.解答题
21.(18分)解方程:
(1)
2x+3(5-x)=4
(2)
(3)
y+1=-y
(4)
(5)
4(x-3)-(3-x)=7(3-x)-(x-3)
(6)
22.(6分)
小明看一本故事书,第一天看了全书的,第二天看了剩下的一半,第三天看了60页刚好看完,这本故事书一共有多少页?
23.(6分)一个三位数和一个两位数的差为225,在三位数的左边写上这个两位数,得到一个五位数,在三位数的右边写上这个两位数,也得到一个五位数,已知前面的五位数比后面的五位数大225,求这个三位数和两位数.
24.(6分)某小区便利店到厂家购进A,B两种香油共140瓶,花了1000元,其中A香油的进价为6.5元/瓶,售价为8元/瓶;B香油的进价为8元/瓶,售价为10元/瓶;
(1)该店购进A,B两种香油各多少瓶?
(2)将购进的140瓶香油全部售完,可获利多少元?
25.(6分)解答下列问题:
(1)一项工作,甲独做需要18天,乙独做需要24天,若两人合做8天后,余下的工作再由甲独做多少天可完成?
(2)甲一天能加工A种零件50个或B种零件20个,1个A种零件与2个B种零件配成一套,那么甲30天时间安排多少天做A种零件,多少天做B种零件,才能使得所有零件都刚好配套?
解题详解
1.
解析:选项A:一元二次方程;选项B:二元一次方程;选项D:分式方程;,故选C
2.
解析:由题可得:m-2≠0,|m|-1=1,解得m-2,故选B
3.
解析:把x=5代入方程,可解得m=-4,故选C
4.
解析:由题可得2(x+3)+3(1-x)=0,解得x=9,故选A
5.
解析:由题可得:|2a+1|=3,解得a=-2或1,故选A
6.
解析:妹妹今年x岁,则哥哥今年2x岁,4年前妹妹(x-4)岁,哥哥(2x-4)岁,由“哥=妹×3”可列方程,故选B
7.
解析:由图可知:2a=3b,2b=3c,则4a=6b,6b=9c,∴4a=9c,故选D.
8.
解析:设负x场,则胜与平的场数都是(x-1)场,由题可得:3(x-1)+(x-1)=8,解得x=3,故选A
9.
解析:设“U”型框的正中间的数为x,则其他6个数分别为x-15、x-13、x-8、x-6、x-1、x+1,则7个数的和为7x-42;其中选项B:7x-42=78,解得x不是整数;故选项B.
10.
解析:设进货价为x元,由等量关系式“利润=进货价×利润率=标价×折扣-进货价”可列方程为:20%x=120×0.9-x,解得x=90,故选C
11.
解析:由图①可得等量关系式:桌高=80-长+宽…①;
由图②可得等量关系式:桌高=70-宽+长…②,
①+②可得:2桌高=70+80,∴桌高=75cm,故选B
12.
解析:假设原价为100元,则提价为110元,应降价(110-100)÷110=%,故选C
13.
解析:
设第一件上衣的成本为x元,由等量关系式“成本×(1+利润率)=售价“可列方程:
(1+20%)x=120,解得x=100;
设第二件上衣的成本为x元,由等量关系式“成本×(1-亏损率)=售价”可列方程:
(1-20%)x=120,解得x=150;
所以,这两件上衣的总成本为250元,总售价为240元,亏损了10元,故选B
14.
解析:由图可得等量关系式:“8个杯子高度-3个杯子高度=5个杯口叠放高度=14-9=5cm”,则可得每2个杯口叠放高度为1cm,由图1可得等量关系式为“1个杯高+3个杯口叠放高度=9cm”,则可得1个杯高为6cm。小明把100个杯子叠放,则等量关系式为:总高度=1个杯高+100个杯口叠放高度=6+100=106cm,故选A
15.
解析:由题可知B所表示的数为5,OB=AB=5,
(1)当P由O---A运动时,
①当P在B点左侧时,由题可知OP=2t,BP=5-2t,则5-2t=2,∴t=;
②当p在B点右侧时,由题可知OP=2t,BP=2t-5,则2t-5=2,∴t=;
(2)当P由A---O运动时,
③当P在B点右侧时,由题可知P点的路程为2t,AP=2t-10,BP=5-(2t-10)=2t+15,则2t+15=2,∴t=;
④当P在B点右侧时,由题可知P点的路程为2t,OP=20-2t,BP=5-(20-2t)=2t-15,则2t-15=2,∴t=;
综上所述,当PB=2时,则运动时间t的值为秒或秒或
秒或秒,故选B
16.
解析:依据是:等式性质二
17.
解析:由题意可得:2a+1+1-3a=0,解得a=2
18.
解析:设有x辆车,由题意可得:4x+8=4.5x,解得x=16,所以这个车队有16辆车
19.
解析:设小正方形的边长为x,则从上下看,大正方形的边长为x+1+2,从左右看,大正方形的边长为4+5-x,由此可列方程为:x+1+2=4+5-x,解得x=3,故小正方形的面积为9.
20.
解析:由条件“火车从开始上桥到过完桥共用了30秒钟”可得等量关系式“600+车长=30×火车速度”;由条件“整列火车完全在桥上的时间为20秒”可得等量关系式“600-车长=20×火车速度”;由火车速度相同可列方程为:,解是x=120,故火车长度为120米.
21.
解析:(1)解:
2x+15-3x=4,2x-3x=4-15,-x=-11,x=11
(2)解:3(x-1)-6=2(4x+1),3x-3-6=8x+2,3x-8x=2+3+6,-5x=11,x=
(3)解:5y+10=2(4y-2)-10y,5y+10=8y-4-10y,5y-8y+10y=-4-10,7y=-14,y=-2
(4)解:,3-x-12-2x=6,-x-2x=6-3+12,-3x=15,x=-5
(5)解:4(x-3)-(3-x)-7(3-x)+(x-3)=0,
4(x-3)+(x-3)+7(x-3)+(x-3)=0,(x-3)(4++7+)=0,∴x-3=0,x=3
(6)解:,70x-3(9-2x)=21,70x-27+6x=21,76x=48,x=
22.
解析:设这本故事书一共x页,则第二天看了全书的(1-)×=,由等量关系式“全书-第一天看的+第二天看的=剩下的60页”可列方程为:x-x-x=60,解得x=150,∴这本故事书一共有150页
23.
解析:设两位数为x,则三位数为x+225,在三位数的左边写上这个两位数所得到一个五位数可表示为:100a+a+225,在三位数的右边写上这个两位数所得到一个五位数可以表示为:100(a+225)+a,由等量关系式“第一个五位数-225=第二个五位数”可列方程为:100a+a+225-225=100(a+225)+a,解得a=25,则a+225=25+225=250,∴这个三位数为250,这个两位数为25
24.
解析:(1)设A种香油有x瓶,则B种香油有(140-x)瓶,由等量关系式“A的总价+B的总价=1000”可列方程为:6.5x+8(140-x)=1000,解得x=80,则140-x=140-80=60,∴该店购进A种香油有80瓶,则B种香油有60瓶;
(2)由等量关系式“总利润=A利润+B利润=A数量×每瓶利润+B数量×每瓶利润”列式为:
(8-6.5)×80+(10-8)×60=240(元),故全部售完可获利240元
25.
解析:(1)设甲独做x天可完成,由等量关系式“8×(甲的工作效率+乙工作效率)+2×甲的工作效率=1”可列方程为:,解得x=4,即余下的工作再由甲独做4天可完成
(2)设安排x天做A种零件,(30-x)天做B种零件,由等量关系式“A总零件:B总零件=1:2,即2×A总零件=B总零件”可列方程为:2×50x=20(30-x),解得x=5,则30-x=30-5=25,∴甲30天时间安排5天做A种零件,25天做B种零件,才能使得所有零件都刚好配套
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
