苏科版七年级上册 《6.3余角、补角、对顶角》强化提优检测(Word版 含答案)
文档属性
| 名称 | 苏科版七年级上册 《6.3余角、补角、对顶角》强化提优检测(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 00:00:00 | ||
图片预览





文档简介
苏科版七年级上《6.3余角、补角、对顶角》强化提优检测
(时间:90分钟
满分:120分)
一.选择题(共20小题
40分)
1.下面4个命题中正确的是(
)
A.相等的两个角是对顶角
B.和等于90
?的两个角互为余角
C.如果∠1+∠2+∠3
=180?,那么∠1,∠2,∠3互为补角
D.一个角的补角一定大于这个角
2.已知∠A=70°,则∠A的补角为( )
A.110°
B.70°
C.30°
D.20°
3.下列选项中,能与30°角互补的是( )
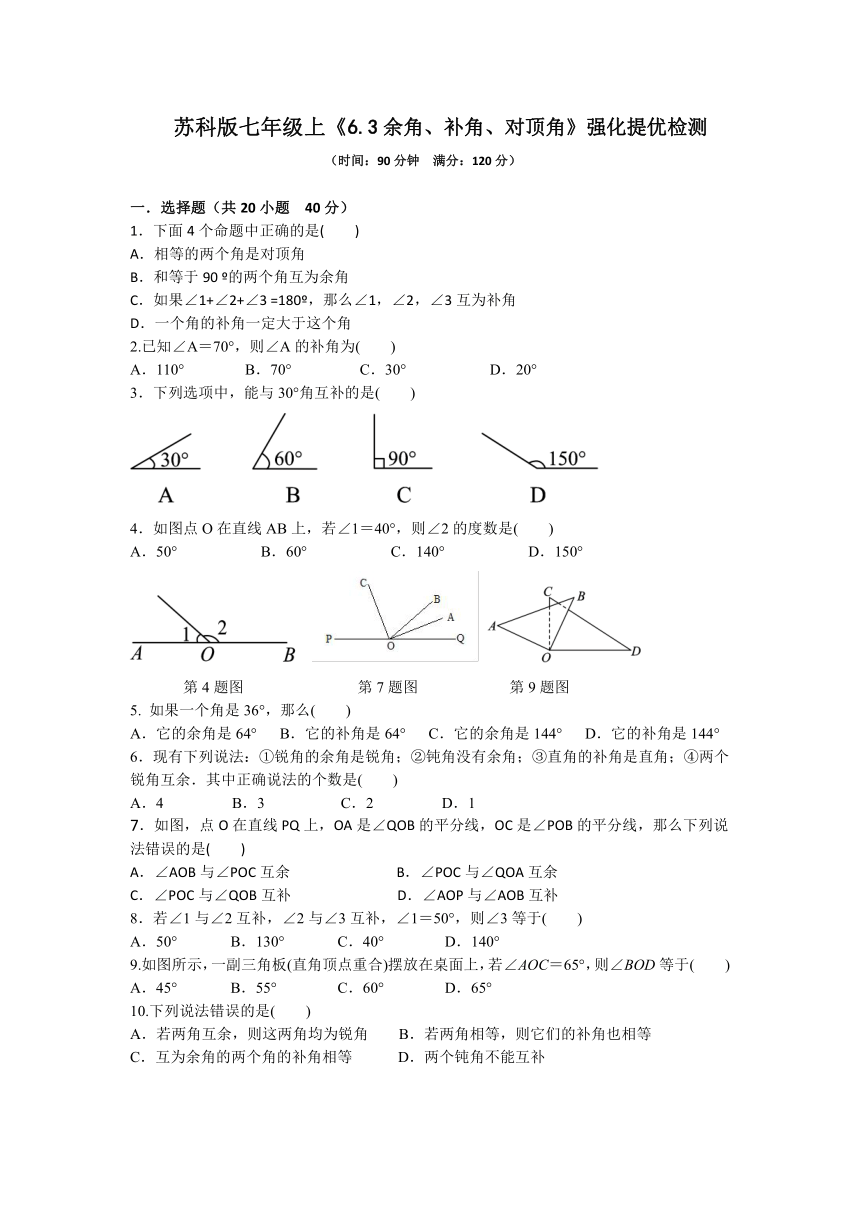
4.如图点O在直线AB上,若∠1=40°,则∠2的度数是( )
A.50°
B.60°
C.140°
D.150°
第4题图
第7题图
第9题图
5.
如果一个角是36°,那么( )
A.它的余角是64°
B.它的补角是64°
C.它的余角是144°
D.它的补角是144°
6.现有下列说法:①锐角的余角是锐角;②钝角没有余角;③直角的补角是直角;④两个锐角互余.其中正确说法的个数是( )
A.4
B.3
C.2
D.1
7.如图,点O在直线PQ上,OA是∠QOB的平分线,OC是∠POB的平分线,那么下列说法错误的是(
)
A.∠AOB与∠POC互余
B.∠POC与∠QOA互余
C.∠POC与∠QOB互补
D.∠AOP与∠AOB互补
8.若∠1与∠2互补,∠2与∠3互补,∠1=50°,则∠3等于( )
A.50°
B.130°
C.40°
D.140°
9.如图所示,一副三角板(直角顶点重合)摆放在桌面上,若∠AOC=65°,则∠BOD等于( )
A.45°
B.55°
C.60°
D.65°
10.下列说法错误的是( )
A.若两角互余,则这两角均为锐角
B.若两角相等,则它们的补角也相等
C.互为余角的两个角的补角相等
D.两个钝角不能互补
11.下列各图中,∠1与∠2是对顶角的是(
)
12.如果一个角等于它的余角的2倍,那么这个角是它的补角的( )
A.2倍
B.
C.5倍
D.
13.已知如图,∠AOB=∠COD=90°,则∠1与∠2的关系是( )
互余
B.互补
C.相等
D.无法确定
第13题图
第14题图
第15题图
第18题图
第19题图
如图,O为直线AB上一点,∠AOC=α,∠BOC=β,则β的余角可表示为( )
A.(α+β)
B.α
C.(α-β)
D.β
15.如图,∠AOC
和∠BOD都是直角,如果∠AOB=140°则∠DOC的度数是(
)
A.30°
B.40°
C.50°
D.60°
16.下列各组角中,∠1与∠2是对顶角的是( )
17.下列说法中,正确的是( )
A.有公共顶点,并且相等的角是对顶角
B.如果两个角不相等,那么它们一定不是对顶角
C.如果两个角相等,那么这两个角是对顶角
D.有的对顶角不相等
18.如图所示,AB与CD相交于点O,∠AOD+∠BOC=280°,则∠AOC的度数为( )
A.40°
B.60°
C.120°
D.140°
19.如图,三条直线l1,l2,l3相交于点E,则∠1+∠2+∠3等于(
)
A.90°
B.120°
C.180°
D.360°
20.已知∠α和∠β互为补角,其中∠α>∠β,那么∠β的余角为(
)
A.(∠α+∠β)
B.(∠α-∠β)
C.∠α
D.不能确定
二.填空题(共15小题
共30分)
21.,则它的余角等于________;∠β的补角是,则=_______.
22.52°34′的余角是__________,补角是__________.
23.若一个锐角的余角与这个角相等,则这个角等于________°.
24.已知∠1和∠2互余,∠2和∠3互补,如果∠1=63°,那么∠3=________°.
25.若∠1+∠2=90°,∠1+∠3=90°,则________=________,理由是__________________________________;若∠1+∠2=180°,∠3+∠4=180°,∠1=∠3,则________=________,理由是_________________________________________________.
26.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC=________°
第26题图
第28题图
第29题图
第31题图
27.已知∠α与∠β互余,且∠α=40°,则∠β的补角为_______度.
28.如图,∠COD为平角,AO⊥OE,∠AOC
=
2∠DOE,则有∠AOC
=__________..
29.
如图,直线AB与CD相交于点O,已知∠AOD=120°,则∠BOC的补角是________°.
30.
若两个角是对顶角且互补,则这两个角都是________角.
31.如图,直线AB,CD相交于点O,OE是∠AOD的平分线,∠COB=140°,则∠DOE=________°.
32.如图,AB,CD相交于点O,∠DOE=90°,∠AOC=72°.
那么∠BOE=_______...
第32题图
第33题图
第34题图
第35题图
33.如图,AB,CD相交于点O,OB平分∠DOE,若∠DOE=60°,那么∠AOC=______..
如图,直线AB、CD相交于点O,∠AOC=34°,∠DOE=56°.
(1)∠BOD=
,∠BOC=
,∠AOE=
.
(2)写出下列各类角的关系:∠BOD和∠EOD
,∠BOD和∠AOC
.
∠BOD和∠AOD
,∠AOC和∠DOE
.
如图,其中共有________对对顶角.
解答题(共10小题
共50分)
36.如图,已知∠BOC=90°,∠DOA=90°,∠1=50°,求∠2的度数.
37.如图所示,点A,O,E在一条直线上,从点O引射线OB,OC,OD,∠AOC=∠COE=∠BOD=90°,那么图中互补的角有哪几对?
.
38.如图,将一副三角尺的直角顶点重合在一起.
(1)若∠DOB与∠DOA的度数之比是2∶11,求∠BOC的度数;
(2)若叠合所成的∠BOC=n°(0<n<90),则∠DOA的补角的度数与∠BOC的度数之比是多少?
39.如图,O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)写出与∠AOE互补的角;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
40.如图,已知O为直线AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°.
(1)∠COD与∠AOB相等吗?请说明理由;
(2)试求∠AOC与∠AOB的度数.
41.如图,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分,且∠BOE∶∠EOD=2∶3,求∠AOE的度数.
42.如图所示,直线AB,CD交于点O,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线.
(1)求∠2和∠3的度数;
(2)OF平分∠AOD吗?请说明理由.
43.所示,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD∶∠BOD=2∶1.
(1)求∠DOE的度数;
(2)求∠AOF的度数.
44.如图,直线AB,CD相交于点O,OE平分∠BOD.
(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠AOE=150°,求∠FOE的度数.
45.观察图,寻找对顶角(不含平角):
(1)如图①,图中共有________对对顶角;
(2)如图②,图中共有________对对顶角;
(3)如图③,图中共有________对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成________对对顶角;
(5)若有2020条直线相交于一点,则可形成多少对对顶角?
教师样卷
一.选择题(共20小题
40分)
1.下面4个命题中正确的是(
)
A.相等的两个角是对顶角
B.和等于90
?的两个角互为余角
C.如果∠1+∠2+∠3
=180?,那么∠1,∠2,∠3互为补角
D.一个角的补角一定大于这个角
【答案】B.
【解析】
A中,如图,∠AOC=∠BOC=90°,但∠AOC与∠BOC不是对顶角,A项错误;B、根据余角的定义,B项正确;C、两个角的和为180°,才能称为互为补角,三个角不可以,C错误;D、钝角的补角是锐角,锐角小于钝角,D错误.
2.已知∠A=70°,则∠A的补角为( )
A.110°
B.70°
C.30°
D.20°
【答案】A
3.下列选项中,能与30°角互补的是( )
【答案】D
4.如图点O在直线AB上,若∠1=40°,则∠2的度数是( )
A.50°
B.60°
C.140°
D.150°
【答案】C
第4题图
第7题图
第9题图
5.
如果一个角是36°,那么( )
A.它的余角是64°
B.它的补角是64°
C.它的余角是144°
D.它的补角是144°
【答案】D [解析]
如果一个角是36°,那么它的余角是90°-36°=54°,补角是180°-36°=144°.故选D.
6.现有下列说法:①锐角的余角是锐角;②钝角没有余角;③直角的补角是直角;④两个锐角互余.其中正确说法的个数是( )
A.4
B.3
C.2
D.1
【答案】B
7.如图,点O在直线PQ上,OA是∠QOB的平分线,OC是∠POB的平分线,那么下列说法错误的是(
)
A.∠AOB与∠POC互余
B.∠POC与∠QOA互余
C.∠POC与∠QOB互补
D.∠AOP与∠AOB互补
【答案】C【解析】
∵OA是∠QOB的平分线,∴∠QOA=∠AOB=∠BOQ,∵OC是∠POB的平分线,∴∠POC=∠BOC=∠POB,∵点O在直线PQ上,∴∠BOQ+∠POB=180°,
A、∠AOB+∠POC=(∠BOQ+∠POB)=×180°=90°,所以,∠AOB与∠POC互余,说法正确,故本选项错误;B、∠POC+∠QOA=(∠BOQ+∠POB)=×180°=90°,所以,∠POC与∠QOA互余,说法正确,故本选项错误;C、∠POC+∠QOB=180°-∠BOC≠180°,所以,∠POC与∠QOB不互补,说法错误,故本选项正确;D、∠AOP+∠AOB=∠AOP+∠AOQ=180°,所以,∠AOP与∠AOB互补,说法正确,故本选项错误.故选C.
8.若∠1与∠2互补,∠2与∠3互补,∠1=50°,则∠3等于( )
A.50°
B.130°
C.40°
D.140°
【答案】A
9.如图所示,一副三角板(直角顶点重合)摆放在桌面上,若∠AOC=65°,则∠BOD等于( )
A.45°
B.55°
C.60°
D.65°
【答案】D [解析]
∵∠AOC和∠BOD都是∠BOC的余角,∴∠AOC=∠BOD.∵∠AOC=65°,∴∠BOD=65°.故选D.
10.下列说法错误的是( )
A.若两角互余,则这两角均为锐角
B.若两角相等,则它们的补角也相等
C.互为余角的两个角的补角相等
D.两个钝角不能互补
【答案】C [解析]
若两角互余,则这两角均为锐角,选项A正确;若两角相等,则它们的补角也相等,选项B正确;30°与60°的角互余,30°角的补角是150°,60°角的补角是120°,则互为余角的两个角的补角不一定相等,选项C错误;两个钝角不能互补,选项D正确
11.下列各图中,∠1与∠2是对顶角的是(
)
【答案】C
【解析】互为对顶角的两个角的两条边互为反向延长线,C中∠1与∠2是对顶角,故选C.
12.如果一个角等于它的余角的2倍,那么这个角是它的补角的( )
A.2倍
B.
C.5倍
D.
【答案】B [解析]
设这个角为α,它的余角为β,它的补角为γ,则α=2β,∵α+β=90°,∴α+α=90°,∴α=60°.∵α+γ=180°,∴γ=120°,∴α=γ.故选B.
13.已知如图,∠AOB=∠COD=90°,则∠1与∠2的关系是( )
互余
B.互补
C.相等
D.无法确定
【答案】B
第13题图
第14题图
第15题图
第18题图
第19题图
如图,O为直线AB上一点,∠AOC=α,∠BOC=β,则β的余角可表示为( )
A.(α+β)
B.α
C.(α-β)
D.β
【答案】C [解析]
由邻补角的定义,得α+β=180°,两边都除以2,得(α+β)=90°,β的余角是(α+β)-β=(α-β).故选C.
15.如图,∠AOC
和∠BOD都是直角,如果∠AOB=140°则∠DOC的度数是(
)
A.30°
B.40°
C.50°
D.60°
【答案】B
【解析】∵∠AOC=∠BOD=90°,∠AOB=140°,∴∠AOD=∠AOB-∠BOD=140°-90°=50°,∴∠DOC=∠AOC-∠AOD=90°-50°=40°.故选B.
16.下列各组角中,∠1与∠2是对顶角的是( )
【答案】D [解析]
根据两条直线相交,才能构成对顶角进行判断,A,B,C都不是由两条直线相交构成的图形,错误;D是由两条直线相交构成的图形,正确.故选D.
17.下列说法中,正确的是( )
A.有公共顶点,并且相等的角是对顶角
B.如果两个角不相等,那么它们一定不是对顶角
C.如果两个角相等,那么这两个角是对顶角
D.有的对顶角不相等
【答案】B
18.如图所示,AB与CD相交于点O,∠AOD+∠BOC=280°,则∠AOC的度数为( )
A.40°
B.60°
C.120°
D.140°
【答案】A [解析]
因为∠AOD与∠BOC是对顶角,所以∠AOD=∠BOC.又因为∠AOD+∠BOC=280°,所以∠AOD=∠BOC=140°.因为∠AOD与∠AOC互补,所以∠AOC=180°-140°=40°.故选A.
19.如图,三条直线l1,l2,l3相交于点E,则∠1+∠2+∠3等于(
)
A.90°
B.120°
C.180°
D.360°
【答案】C
20.已知∠α和∠β互为补角,其中∠α>∠β,那么∠β的余角为(
)
A.(∠α+∠β)
B.(∠α-∠β)
C.∠α
D.不能确定
【答案】B
【解析】∵∠1,∠2互为补角∴∠α+∠β=180°∴∠β的余角是90-∠β=
(∠α+∠β)-∠β=
(∠α-∠β).故选B.
二.填空题(共15小题
共30分)
21.,则它的余角等于________;∠β的补角是,则=_______.
【答案】,.
【解析】余角=90°-∠α=90°-=,∠β=180°-=.
22.52°34′的余角是__________,补角是__________.
【答案】.37°26′ 127°26′ [解析]
90°-52°34′=37°26′,180°-52°34′=127°26′.
23.若一个锐角的余角与这个角相等,则这个角等于________°.
【答案】.45
24.已知∠1和∠2互余,∠2和∠3互补,如果∠1=63°,那么∠3=________°.
【答案】.153 [解析]
因为∠1和∠2互余,所以∠1+∠2=90°.又因为∠1=63°,所以∠2=27°.因为∠2和∠3互补,所以∠2+∠3=180°,即27°+∠3=180°,所以∠3=153°.
25.若∠1+∠2=90°,∠1+∠3=90°,则________=________,理由是__________________________________;若∠1+∠2=180°,∠3+∠4=180°,∠1=∠3,则________=________,理由是_________________________________________________.
【答案】1.∠2 ∠3 同角的余角相等 ∠2 ∠4
26.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC=________°
【答案】30 [解析]
∵∠AOB=∠COD=90°,∠AOD=150°,∴∠BOC=∠AOB+∠COD-∠AOD=90°+90°-150°=30°.
第26题图
第28题图
第29题图
第31题图
27.已知∠α与∠β互余,且∠α=40°,则∠β的补角为_______度.
【答案】130.【解析】∵∠α与∠β互余,且∠α=40°,∴∠β=90-∠α=90°-40°=50°;
∴∠β的补角为180°-50°=130°.故填130.
28.如图,∠COD为平角,AO⊥OE,∠AOC
=
2∠DOE,则有∠AOC
=__________.
【答案】60°.
【解析】∵∠COD为平角,AO⊥OE,∴∠AOC+∠DOE=∠COD-∠AOE=180°-90°=90°.又∵∠AOC=2∠DOE,∴∠AOC=?×90°=60°.故填60°.
29.
如图,直线AB与CD相交于点O,已知∠AOD=120°,则∠BOC的补角是________°.
【答案】60 [解析]
因为∠AOD与∠BOC为对顶角,所以∠AOD=∠BOC=120°,故∠BOC的补角为180°-120°=60°.
30.
若两个角是对顶角且互补,则这两个角都是________角.
【答案】.直 [解析]
因为两个角是对顶角,所以这两个角相等.因为这两个角互补,所以它们的度数之和为180°,所以这两个角都是90°,都是直角.
31.如图,直线AB,CD相交于点O,OE是∠AOD的平分线,∠COB=140°,则∠DOE=________°.
【答案】70 [解析]
∵∠COB=140°,∴∠AOD=140°,∵OE是∠AOD的平分线,
∴∠DOE=∠AOE=70°.
32.如图,AB,CD相交于点O,∠DOE=90°,∠AOC=72°.
那么∠BOE=_______..
【答案】18O.解:因为∠BOD与∠AOC是对顶角,∠AOC=72°,所以∠BOD=∠AOC=72°.因为∠DOE=90°,所以∠BOE=∠DOE-∠BOD
=90°-72°=18°.
第32题图
第33题图
第34题图
第35题图
33.如图,AB,CD相交于点O,OB平分∠DOE,若∠DOE=60°,那么∠AOC=______..
【答案】30°
解:∵OB平分∠DOE,∠DOE=60°,∴∠BOD=∠DOE=×60°=30°,∴∠AOC=∠BOD=30°
如图,直线AB、CD相交于点O,∠AOC=34°,∠DOE=56°.
(1)∠BOD=
,∠BOC=
,∠AOE=
.
(2)写出下列各类角的关系:∠BOD和∠EOD
,∠BOD和∠AOC
.
∠BOD和∠AOD
,∠AOC和∠DOE
.
【答案】(1)34°,146°,90°;(2)互余,对顶角,互补,互余
【解析】(1)∵∠AOC=34°,∠AOC+∠BOC=180°,∠BOD+∠BOC=180°,∴∠BOD=∠AOC=34°,∠BOC=180°-34°=146°∵∠BOD=34°,∠DOE=56°,∴∠BOE=90°,∵∠AOE+∠BOE=180°,∴∠AOE=90°;(2)互余,对顶角,互补,互余.
35.如图,其中共有________对对顶角.
【答案】4
【解析】4对对顶角中有:∠BHF与∠CHG,∠BHC与∠FHG,∠BCH与∠DCE,∠BCE与∠DCH.
解答题(共10小题
共50分)
36.如图,已知∠BOC=90°,∠DOA=90°,∠1=50°,求∠2的度数.
解:因为∠AOD=90°,所以∠1+∠BOD=90°.
因为∠BOC=90°,所以∠2+∠BOD=90°.根据同角的余角相等,可得∠2=∠1=50°.
37.如图所示,点A,O,E在一条直线上,从点O引射线OB,OC,OD,∠AOC=∠COE=∠BOD=90°,那么图中互补的角有哪几对?
解:∠AOD与∠DOE互补,∠BOC与∠DOE互补,∠BOE与∠AOB互补,∠DOC与∠AOB互补,∠AOC与∠BOD互补,∠AOC与∠COE互补,∠BOD与∠COE互补.
38.如图,将一副三角尺的直角顶点重合在一起.
(1)若∠DOB与∠DOA的度数之比是2∶11,求∠BOC的度数;
(2)若叠合所成的∠BOC=n°(0<n<90),则∠DOA的补角的度数与∠BOC的度数之比是多少?
解:(1)设∠DOB=2x,则∠DOA=11x.
因为∠AOB=∠COD=90°,
所以∠AOC=∠DOB=2x,∠BOC=7x.
又因为∠DOA=∠AOB+∠COD-∠BOC=180°-∠BOC,
可得方程11x=180°-7x,解得x=10°,
所以∠BOC=70°.
(2)因为∠DOA=∠AOB+∠COD-∠BOC=180°-∠BOC,
所以∠DOA与∠BOC互补,
则∠DOA的补角的度数是n°,
则∠DOA的补角的度数与∠BOC的度数之比是1∶1.
39.如图,O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)写出与∠AOE互补的角;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
解:(1)∵OE平分∠BOC,
∴∠BOE=∠COE.
∵∠AOE+∠BOE=180°,
∴∠AOE+∠COE=180°,
∴与∠AOE互补的角是∠BOE,∠COE.
(2)∵OD,OE分别平分∠AOC,∠BOC,
∴∠COD=∠AOD=36°,∠COE=∠BOE=∠BOC,∠AOC=2×36°=72°,
∴∠BOC=180°-72°=108°,
∴∠COE=∠BOC=54°,
∴∠DOE=∠COD+∠COE=90°.
(3)当∠AOD=x°时,∠DOE=90°.
40.如图,已知O为直线AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°.
(1)∠COD与∠AOB相等吗?请说明理由;
(2)试求∠AOC与∠AOB的度数.
解:(1)∠COD=∠AOB.理由:因为∠AOC与∠AOB互补,所以∠AOC+∠AOB=180°.又因为∠AOC+∠COD=180°,所以∠COD=∠AOB.
(2)因为OM和ON分别是∠AOC和∠AOB的平分线,
所以∠AOM=∠AOC,∠AON=∠AOB,
所以∠MON=∠AOM-∠AON=∠AOC-∠AOB=(∠AOC-∠AOB)=∠BOC.
因为∠MON=40°,所以∠BOC=80°,
所以∠COD+∠AOB=180°-80°=100°.
又因为∠AOB=∠COD,
所以∠AOB=∠COD=50°,
所以∠AOC=180°-∠COD=130°.
41.如图,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分,且∠BOE∶∠EOD=2∶3,求∠AOE的度数.
解:因为∠AOC=70°,
所以∠BOD=∠AOC=70°.
因为∠BOE∶∠EOD=2∶3,
所以∠BOE=×70°=28°,
所以∠AOE=180°-28°=152°.
42.如图所示,直线AB,CD交于点O,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线.
(1)求∠2和∠3的度数;
(2)OF平分∠AOD吗?请说明理由.
解:(1)因为∠BOC=80°,OE平分∠BOC,所以∠1=∠COE=40°.根据对顶角相等,可得∠3=∠COE=40°.根据平角的定义,可得∠2=180°-40°-40°=100°.
(2)OF平分∠AOD.理由:根据对顶角相等,可得∠AOF=∠1=40°.又因为∠3=40°,所以OF平分∠AOD.
43.所示,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD∶∠BOD=2∶1.
(1)求∠DOE的度数;
(2)求∠AOF的度数.
解:(1)∵∠AOD∶∠BOD=2∶1,∠AOD+∠BOD=180°,
∴∠BOD=×180°=60°.
∵OE平分∠BOD,
∴∠DOE=∠BOD=×60°=30°.
(2)∠COE=∠COD-∠DOE=180°-30°=150°.
∵OF平分∠COE,
∴∠COF=∠COE=×150°=75°.
∵∠AOC=∠BOD=60°(对顶角相等),
∴∠AOF=∠AOC+∠COF=60°+75°=135°.
44.如图,直线AB,CD相交于点O,OE平分∠BOD.
(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠AOE=150°,求∠FOE的度数.
解:(1)∵∠AOC=68°,∴∠BOD=68°.
∵OE平分∠BOD,
∴∠BOE=∠DOE=34°.
∵∠DOF=90°,
∴∠EOF=∠DOF-∠DOE=90°-34°=56°.
(2)∵OE平分∠BOD,
∴∠BOE=∠DOE.
∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,
∴∠COE=∠AOE=150°.
∵OF平分∠COE,
∴∠FOE=∠COE=×150°=75°.
45.观察图,寻找对顶角(不含平角):
(1)如图①,图中共有________对对顶角;
(2)如图②,图中共有________对对顶角;
(3)如图③,图中共有________对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成________对对顶角;
(5)若有2020条直线相交于一点,则可形成多少对对顶角?
解:(1)如图①,图中共有1×2=2(对)对顶角.
(2)如图②,图中共有2×3=6(对)对顶角.
(3)如图③,图中共有3×4=12(对)对顶角.
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,
若有n条直线相交于一点,则可形成n(n-1)对对顶角.
(5)若有2030条直线相交于一点,则可形成(2020-1)×2020=4078380(对)对顶角.
(时间:90分钟
满分:120分)
一.选择题(共20小题
40分)
1.下面4个命题中正确的是(
)
A.相等的两个角是对顶角
B.和等于90
?的两个角互为余角
C.如果∠1+∠2+∠3
=180?,那么∠1,∠2,∠3互为补角
D.一个角的补角一定大于这个角
2.已知∠A=70°,则∠A的补角为( )
A.110°
B.70°
C.30°
D.20°
3.下列选项中,能与30°角互补的是( )
4.如图点O在直线AB上,若∠1=40°,则∠2的度数是( )
A.50°
B.60°
C.140°
D.150°
第4题图
第7题图
第9题图
5.
如果一个角是36°,那么( )
A.它的余角是64°
B.它的补角是64°
C.它的余角是144°
D.它的补角是144°
6.现有下列说法:①锐角的余角是锐角;②钝角没有余角;③直角的补角是直角;④两个锐角互余.其中正确说法的个数是( )
A.4
B.3
C.2
D.1
7.如图,点O在直线PQ上,OA是∠QOB的平分线,OC是∠POB的平分线,那么下列说法错误的是(
)
A.∠AOB与∠POC互余
B.∠POC与∠QOA互余
C.∠POC与∠QOB互补
D.∠AOP与∠AOB互补
8.若∠1与∠2互补,∠2与∠3互补,∠1=50°,则∠3等于( )
A.50°
B.130°
C.40°
D.140°
9.如图所示,一副三角板(直角顶点重合)摆放在桌面上,若∠AOC=65°,则∠BOD等于( )
A.45°
B.55°
C.60°
D.65°
10.下列说法错误的是( )
A.若两角互余,则这两角均为锐角
B.若两角相等,则它们的补角也相等
C.互为余角的两个角的补角相等
D.两个钝角不能互补
11.下列各图中,∠1与∠2是对顶角的是(
)
12.如果一个角等于它的余角的2倍,那么这个角是它的补角的( )
A.2倍
B.
C.5倍
D.
13.已知如图,∠AOB=∠COD=90°,则∠1与∠2的关系是( )
互余
B.互补
C.相等
D.无法确定
第13题图
第14题图
第15题图
第18题图
第19题图
如图,O为直线AB上一点,∠AOC=α,∠BOC=β,则β的余角可表示为( )
A.(α+β)
B.α
C.(α-β)
D.β
15.如图,∠AOC
和∠BOD都是直角,如果∠AOB=140°则∠DOC的度数是(
)
A.30°
B.40°
C.50°
D.60°
16.下列各组角中,∠1与∠2是对顶角的是( )
17.下列说法中,正确的是( )
A.有公共顶点,并且相等的角是对顶角
B.如果两个角不相等,那么它们一定不是对顶角
C.如果两个角相等,那么这两个角是对顶角
D.有的对顶角不相等
18.如图所示,AB与CD相交于点O,∠AOD+∠BOC=280°,则∠AOC的度数为( )
A.40°
B.60°
C.120°
D.140°
19.如图,三条直线l1,l2,l3相交于点E,则∠1+∠2+∠3等于(
)
A.90°
B.120°
C.180°
D.360°
20.已知∠α和∠β互为补角,其中∠α>∠β,那么∠β的余角为(
)
A.(∠α+∠β)
B.(∠α-∠β)
C.∠α
D.不能确定
二.填空题(共15小题
共30分)
21.,则它的余角等于________;∠β的补角是,则=_______.
22.52°34′的余角是__________,补角是__________.
23.若一个锐角的余角与这个角相等,则这个角等于________°.
24.已知∠1和∠2互余,∠2和∠3互补,如果∠1=63°,那么∠3=________°.
25.若∠1+∠2=90°,∠1+∠3=90°,则________=________,理由是__________________________________;若∠1+∠2=180°,∠3+∠4=180°,∠1=∠3,则________=________,理由是_________________________________________________.
26.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC=________°
第26题图
第28题图
第29题图
第31题图
27.已知∠α与∠β互余,且∠α=40°,则∠β的补角为_______度.
28.如图,∠COD为平角,AO⊥OE,∠AOC
=
2∠DOE,则有∠AOC
=__________..
29.
如图,直线AB与CD相交于点O,已知∠AOD=120°,则∠BOC的补角是________°.
30.
若两个角是对顶角且互补,则这两个角都是________角.
31.如图,直线AB,CD相交于点O,OE是∠AOD的平分线,∠COB=140°,则∠DOE=________°.
32.如图,AB,CD相交于点O,∠DOE=90°,∠AOC=72°.
那么∠BOE=_______...
第32题图
第33题图
第34题图
第35题图
33.如图,AB,CD相交于点O,OB平分∠DOE,若∠DOE=60°,那么∠AOC=______..
如图,直线AB、CD相交于点O,∠AOC=34°,∠DOE=56°.
(1)∠BOD=
,∠BOC=
,∠AOE=
.
(2)写出下列各类角的关系:∠BOD和∠EOD
,∠BOD和∠AOC
.
∠BOD和∠AOD
,∠AOC和∠DOE
.
如图,其中共有________对对顶角.
解答题(共10小题
共50分)
36.如图,已知∠BOC=90°,∠DOA=90°,∠1=50°,求∠2的度数.
37.如图所示,点A,O,E在一条直线上,从点O引射线OB,OC,OD,∠AOC=∠COE=∠BOD=90°,那么图中互补的角有哪几对?
.
38.如图,将一副三角尺的直角顶点重合在一起.
(1)若∠DOB与∠DOA的度数之比是2∶11,求∠BOC的度数;
(2)若叠合所成的∠BOC=n°(0<n<90),则∠DOA的补角的度数与∠BOC的度数之比是多少?
39.如图,O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)写出与∠AOE互补的角;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
40.如图,已知O为直线AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°.
(1)∠COD与∠AOB相等吗?请说明理由;
(2)试求∠AOC与∠AOB的度数.
41.如图,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分,且∠BOE∶∠EOD=2∶3,求∠AOE的度数.
42.如图所示,直线AB,CD交于点O,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线.
(1)求∠2和∠3的度数;
(2)OF平分∠AOD吗?请说明理由.
43.所示,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD∶∠BOD=2∶1.
(1)求∠DOE的度数;
(2)求∠AOF的度数.
44.如图,直线AB,CD相交于点O,OE平分∠BOD.
(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠AOE=150°,求∠FOE的度数.
45.观察图,寻找对顶角(不含平角):
(1)如图①,图中共有________对对顶角;
(2)如图②,图中共有________对对顶角;
(3)如图③,图中共有________对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成________对对顶角;
(5)若有2020条直线相交于一点,则可形成多少对对顶角?
教师样卷
一.选择题(共20小题
40分)
1.下面4个命题中正确的是(
)
A.相等的两个角是对顶角
B.和等于90
?的两个角互为余角
C.如果∠1+∠2+∠3
=180?,那么∠1,∠2,∠3互为补角
D.一个角的补角一定大于这个角
【答案】B.
【解析】
A中,如图,∠AOC=∠BOC=90°,但∠AOC与∠BOC不是对顶角,A项错误;B、根据余角的定义,B项正确;C、两个角的和为180°,才能称为互为补角,三个角不可以,C错误;D、钝角的补角是锐角,锐角小于钝角,D错误.
2.已知∠A=70°,则∠A的补角为( )
A.110°
B.70°
C.30°
D.20°
【答案】A
3.下列选项中,能与30°角互补的是( )
【答案】D
4.如图点O在直线AB上,若∠1=40°,则∠2的度数是( )
A.50°
B.60°
C.140°
D.150°
【答案】C
第4题图
第7题图
第9题图
5.
如果一个角是36°,那么( )
A.它的余角是64°
B.它的补角是64°
C.它的余角是144°
D.它的补角是144°
【答案】D [解析]
如果一个角是36°,那么它的余角是90°-36°=54°,补角是180°-36°=144°.故选D.
6.现有下列说法:①锐角的余角是锐角;②钝角没有余角;③直角的补角是直角;④两个锐角互余.其中正确说法的个数是( )
A.4
B.3
C.2
D.1
【答案】B
7.如图,点O在直线PQ上,OA是∠QOB的平分线,OC是∠POB的平分线,那么下列说法错误的是(
)
A.∠AOB与∠POC互余
B.∠POC与∠QOA互余
C.∠POC与∠QOB互补
D.∠AOP与∠AOB互补
【答案】C【解析】
∵OA是∠QOB的平分线,∴∠QOA=∠AOB=∠BOQ,∵OC是∠POB的平分线,∴∠POC=∠BOC=∠POB,∵点O在直线PQ上,∴∠BOQ+∠POB=180°,
A、∠AOB+∠POC=(∠BOQ+∠POB)=×180°=90°,所以,∠AOB与∠POC互余,说法正确,故本选项错误;B、∠POC+∠QOA=(∠BOQ+∠POB)=×180°=90°,所以,∠POC与∠QOA互余,说法正确,故本选项错误;C、∠POC+∠QOB=180°-∠BOC≠180°,所以,∠POC与∠QOB不互补,说法错误,故本选项正确;D、∠AOP+∠AOB=∠AOP+∠AOQ=180°,所以,∠AOP与∠AOB互补,说法正确,故本选项错误.故选C.
8.若∠1与∠2互补,∠2与∠3互补,∠1=50°,则∠3等于( )
A.50°
B.130°
C.40°
D.140°
【答案】A
9.如图所示,一副三角板(直角顶点重合)摆放在桌面上,若∠AOC=65°,则∠BOD等于( )
A.45°
B.55°
C.60°
D.65°
【答案】D [解析]
∵∠AOC和∠BOD都是∠BOC的余角,∴∠AOC=∠BOD.∵∠AOC=65°,∴∠BOD=65°.故选D.
10.下列说法错误的是( )
A.若两角互余,则这两角均为锐角
B.若两角相等,则它们的补角也相等
C.互为余角的两个角的补角相等
D.两个钝角不能互补
【答案】C [解析]
若两角互余,则这两角均为锐角,选项A正确;若两角相等,则它们的补角也相等,选项B正确;30°与60°的角互余,30°角的补角是150°,60°角的补角是120°,则互为余角的两个角的补角不一定相等,选项C错误;两个钝角不能互补,选项D正确
11.下列各图中,∠1与∠2是对顶角的是(
)
【答案】C
【解析】互为对顶角的两个角的两条边互为反向延长线,C中∠1与∠2是对顶角,故选C.
12.如果一个角等于它的余角的2倍,那么这个角是它的补角的( )
A.2倍
B.
C.5倍
D.
【答案】B [解析]
设这个角为α,它的余角为β,它的补角为γ,则α=2β,∵α+β=90°,∴α+α=90°,∴α=60°.∵α+γ=180°,∴γ=120°,∴α=γ.故选B.
13.已知如图,∠AOB=∠COD=90°,则∠1与∠2的关系是( )
互余
B.互补
C.相等
D.无法确定
【答案】B
第13题图
第14题图
第15题图
第18题图
第19题图
如图,O为直线AB上一点,∠AOC=α,∠BOC=β,则β的余角可表示为( )
A.(α+β)
B.α
C.(α-β)
D.β
【答案】C [解析]
由邻补角的定义,得α+β=180°,两边都除以2,得(α+β)=90°,β的余角是(α+β)-β=(α-β).故选C.
15.如图,∠AOC
和∠BOD都是直角,如果∠AOB=140°则∠DOC的度数是(
)
A.30°
B.40°
C.50°
D.60°
【答案】B
【解析】∵∠AOC=∠BOD=90°,∠AOB=140°,∴∠AOD=∠AOB-∠BOD=140°-90°=50°,∴∠DOC=∠AOC-∠AOD=90°-50°=40°.故选B.
16.下列各组角中,∠1与∠2是对顶角的是( )
【答案】D [解析]
根据两条直线相交,才能构成对顶角进行判断,A,B,C都不是由两条直线相交构成的图形,错误;D是由两条直线相交构成的图形,正确.故选D.
17.下列说法中,正确的是( )
A.有公共顶点,并且相等的角是对顶角
B.如果两个角不相等,那么它们一定不是对顶角
C.如果两个角相等,那么这两个角是对顶角
D.有的对顶角不相等
【答案】B
18.如图所示,AB与CD相交于点O,∠AOD+∠BOC=280°,则∠AOC的度数为( )
A.40°
B.60°
C.120°
D.140°
【答案】A [解析]
因为∠AOD与∠BOC是对顶角,所以∠AOD=∠BOC.又因为∠AOD+∠BOC=280°,所以∠AOD=∠BOC=140°.因为∠AOD与∠AOC互补,所以∠AOC=180°-140°=40°.故选A.
19.如图,三条直线l1,l2,l3相交于点E,则∠1+∠2+∠3等于(
)
A.90°
B.120°
C.180°
D.360°
【答案】C
20.已知∠α和∠β互为补角,其中∠α>∠β,那么∠β的余角为(
)
A.(∠α+∠β)
B.(∠α-∠β)
C.∠α
D.不能确定
【答案】B
【解析】∵∠1,∠2互为补角∴∠α+∠β=180°∴∠β的余角是90-∠β=
(∠α+∠β)-∠β=
(∠α-∠β).故选B.
二.填空题(共15小题
共30分)
21.,则它的余角等于________;∠β的补角是,则=_______.
【答案】,.
【解析】余角=90°-∠α=90°-=,∠β=180°-=.
22.52°34′的余角是__________,补角是__________.
【答案】.37°26′ 127°26′ [解析]
90°-52°34′=37°26′,180°-52°34′=127°26′.
23.若一个锐角的余角与这个角相等,则这个角等于________°.
【答案】.45
24.已知∠1和∠2互余,∠2和∠3互补,如果∠1=63°,那么∠3=________°.
【答案】.153 [解析]
因为∠1和∠2互余,所以∠1+∠2=90°.又因为∠1=63°,所以∠2=27°.因为∠2和∠3互补,所以∠2+∠3=180°,即27°+∠3=180°,所以∠3=153°.
25.若∠1+∠2=90°,∠1+∠3=90°,则________=________,理由是__________________________________;若∠1+∠2=180°,∠3+∠4=180°,∠1=∠3,则________=________,理由是_________________________________________________.
【答案】1.∠2 ∠3 同角的余角相等 ∠2 ∠4
26.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC=________°
【答案】30 [解析]
∵∠AOB=∠COD=90°,∠AOD=150°,∴∠BOC=∠AOB+∠COD-∠AOD=90°+90°-150°=30°.
第26题图
第28题图
第29题图
第31题图
27.已知∠α与∠β互余,且∠α=40°,则∠β的补角为_______度.
【答案】130.【解析】∵∠α与∠β互余,且∠α=40°,∴∠β=90-∠α=90°-40°=50°;
∴∠β的补角为180°-50°=130°.故填130.
28.如图,∠COD为平角,AO⊥OE,∠AOC
=
2∠DOE,则有∠AOC
=__________.
【答案】60°.
【解析】∵∠COD为平角,AO⊥OE,∴∠AOC+∠DOE=∠COD-∠AOE=180°-90°=90°.又∵∠AOC=2∠DOE,∴∠AOC=?×90°=60°.故填60°.
29.
如图,直线AB与CD相交于点O,已知∠AOD=120°,则∠BOC的补角是________°.
【答案】60 [解析]
因为∠AOD与∠BOC为对顶角,所以∠AOD=∠BOC=120°,故∠BOC的补角为180°-120°=60°.
30.
若两个角是对顶角且互补,则这两个角都是________角.
【答案】.直 [解析]
因为两个角是对顶角,所以这两个角相等.因为这两个角互补,所以它们的度数之和为180°,所以这两个角都是90°,都是直角.
31.如图,直线AB,CD相交于点O,OE是∠AOD的平分线,∠COB=140°,则∠DOE=________°.
【答案】70 [解析]
∵∠COB=140°,∴∠AOD=140°,∵OE是∠AOD的平分线,
∴∠DOE=∠AOE=70°.
32.如图,AB,CD相交于点O,∠DOE=90°,∠AOC=72°.
那么∠BOE=_______..
【答案】18O.解:因为∠BOD与∠AOC是对顶角,∠AOC=72°,所以∠BOD=∠AOC=72°.因为∠DOE=90°,所以∠BOE=∠DOE-∠BOD
=90°-72°=18°.
第32题图
第33题图
第34题图
第35题图
33.如图,AB,CD相交于点O,OB平分∠DOE,若∠DOE=60°,那么∠AOC=______..
【答案】30°
解:∵OB平分∠DOE,∠DOE=60°,∴∠BOD=∠DOE=×60°=30°,∴∠AOC=∠BOD=30°
如图,直线AB、CD相交于点O,∠AOC=34°,∠DOE=56°.
(1)∠BOD=
,∠BOC=
,∠AOE=
.
(2)写出下列各类角的关系:∠BOD和∠EOD
,∠BOD和∠AOC
.
∠BOD和∠AOD
,∠AOC和∠DOE
.
【答案】(1)34°,146°,90°;(2)互余,对顶角,互补,互余
【解析】(1)∵∠AOC=34°,∠AOC+∠BOC=180°,∠BOD+∠BOC=180°,∴∠BOD=∠AOC=34°,∠BOC=180°-34°=146°∵∠BOD=34°,∠DOE=56°,∴∠BOE=90°,∵∠AOE+∠BOE=180°,∴∠AOE=90°;(2)互余,对顶角,互补,互余.
35.如图,其中共有________对对顶角.
【答案】4
【解析】4对对顶角中有:∠BHF与∠CHG,∠BHC与∠FHG,∠BCH与∠DCE,∠BCE与∠DCH.
解答题(共10小题
共50分)
36.如图,已知∠BOC=90°,∠DOA=90°,∠1=50°,求∠2的度数.
解:因为∠AOD=90°,所以∠1+∠BOD=90°.
因为∠BOC=90°,所以∠2+∠BOD=90°.根据同角的余角相等,可得∠2=∠1=50°.
37.如图所示,点A,O,E在一条直线上,从点O引射线OB,OC,OD,∠AOC=∠COE=∠BOD=90°,那么图中互补的角有哪几对?
解:∠AOD与∠DOE互补,∠BOC与∠DOE互补,∠BOE与∠AOB互补,∠DOC与∠AOB互补,∠AOC与∠BOD互补,∠AOC与∠COE互补,∠BOD与∠COE互补.
38.如图,将一副三角尺的直角顶点重合在一起.
(1)若∠DOB与∠DOA的度数之比是2∶11,求∠BOC的度数;
(2)若叠合所成的∠BOC=n°(0<n<90),则∠DOA的补角的度数与∠BOC的度数之比是多少?
解:(1)设∠DOB=2x,则∠DOA=11x.
因为∠AOB=∠COD=90°,
所以∠AOC=∠DOB=2x,∠BOC=7x.
又因为∠DOA=∠AOB+∠COD-∠BOC=180°-∠BOC,
可得方程11x=180°-7x,解得x=10°,
所以∠BOC=70°.
(2)因为∠DOA=∠AOB+∠COD-∠BOC=180°-∠BOC,
所以∠DOA与∠BOC互补,
则∠DOA的补角的度数是n°,
则∠DOA的补角的度数与∠BOC的度数之比是1∶1.
39.如图,O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)写出与∠AOE互补的角;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
解:(1)∵OE平分∠BOC,
∴∠BOE=∠COE.
∵∠AOE+∠BOE=180°,
∴∠AOE+∠COE=180°,
∴与∠AOE互补的角是∠BOE,∠COE.
(2)∵OD,OE分别平分∠AOC,∠BOC,
∴∠COD=∠AOD=36°,∠COE=∠BOE=∠BOC,∠AOC=2×36°=72°,
∴∠BOC=180°-72°=108°,
∴∠COE=∠BOC=54°,
∴∠DOE=∠COD+∠COE=90°.
(3)当∠AOD=x°时,∠DOE=90°.
40.如图,已知O为直线AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°.
(1)∠COD与∠AOB相等吗?请说明理由;
(2)试求∠AOC与∠AOB的度数.
解:(1)∠COD=∠AOB.理由:因为∠AOC与∠AOB互补,所以∠AOC+∠AOB=180°.又因为∠AOC+∠COD=180°,所以∠COD=∠AOB.
(2)因为OM和ON分别是∠AOC和∠AOB的平分线,
所以∠AOM=∠AOC,∠AON=∠AOB,
所以∠MON=∠AOM-∠AON=∠AOC-∠AOB=(∠AOC-∠AOB)=∠BOC.
因为∠MON=40°,所以∠BOC=80°,
所以∠COD+∠AOB=180°-80°=100°.
又因为∠AOB=∠COD,
所以∠AOB=∠COD=50°,
所以∠AOC=180°-∠COD=130°.
41.如图,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分,且∠BOE∶∠EOD=2∶3,求∠AOE的度数.
解:因为∠AOC=70°,
所以∠BOD=∠AOC=70°.
因为∠BOE∶∠EOD=2∶3,
所以∠BOE=×70°=28°,
所以∠AOE=180°-28°=152°.
42.如图所示,直线AB,CD交于点O,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线.
(1)求∠2和∠3的度数;
(2)OF平分∠AOD吗?请说明理由.
解:(1)因为∠BOC=80°,OE平分∠BOC,所以∠1=∠COE=40°.根据对顶角相等,可得∠3=∠COE=40°.根据平角的定义,可得∠2=180°-40°-40°=100°.
(2)OF平分∠AOD.理由:根据对顶角相等,可得∠AOF=∠1=40°.又因为∠3=40°,所以OF平分∠AOD.
43.所示,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD∶∠BOD=2∶1.
(1)求∠DOE的度数;
(2)求∠AOF的度数.
解:(1)∵∠AOD∶∠BOD=2∶1,∠AOD+∠BOD=180°,
∴∠BOD=×180°=60°.
∵OE平分∠BOD,
∴∠DOE=∠BOD=×60°=30°.
(2)∠COE=∠COD-∠DOE=180°-30°=150°.
∵OF平分∠COE,
∴∠COF=∠COE=×150°=75°.
∵∠AOC=∠BOD=60°(对顶角相等),
∴∠AOF=∠AOC+∠COF=60°+75°=135°.
44.如图,直线AB,CD相交于点O,OE平分∠BOD.
(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠AOE=150°,求∠FOE的度数.
解:(1)∵∠AOC=68°,∴∠BOD=68°.
∵OE平分∠BOD,
∴∠BOE=∠DOE=34°.
∵∠DOF=90°,
∴∠EOF=∠DOF-∠DOE=90°-34°=56°.
(2)∵OE平分∠BOD,
∴∠BOE=∠DOE.
∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,
∴∠COE=∠AOE=150°.
∵OF平分∠COE,
∴∠FOE=∠COE=×150°=75°.
45.观察图,寻找对顶角(不含平角):
(1)如图①,图中共有________对对顶角;
(2)如图②,图中共有________对对顶角;
(3)如图③,图中共有________对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成________对对顶角;
(5)若有2020条直线相交于一点,则可形成多少对对顶角?
解:(1)如图①,图中共有1×2=2(对)对顶角.
(2)如图②,图中共有2×3=6(对)对顶角.
(3)如图③,图中共有3×4=12(对)对顶角.
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,
若有n条直线相交于一点,则可形成n(n-1)对对顶角.
(5)若有2030条直线相交于一点,则可形成(2020-1)×2020=4078380(对)对顶角.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
