人教版八年级数学上册教学设计:12.2 全等三角形的判定—ASA(表格式)
文档属性
| 名称 | 人教版八年级数学上册教学设计:12.2 全等三角形的判定—ASA(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 176.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 00:00:00 | ||
图片预览


文档简介
八年级数学上册教学设计
课题
12.2
全等三角形的判定—ASA
教学
目标
1.理解ASA证明两个三角形全等的内容,并能应用ASA证明两个三角形全等。
2.用ASA证明两个三角形全等,明确这里的边为两个角的夹边
教学
重点
根据条件添加适当的条件使三角形全等。
教学
难点
应用ASA证明两个三角形全等
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、全等三角形的第三种判定方法:
归纳:两角和它们的分别相等的两个三角形全等。
(简称或)
用符号语言表达为:
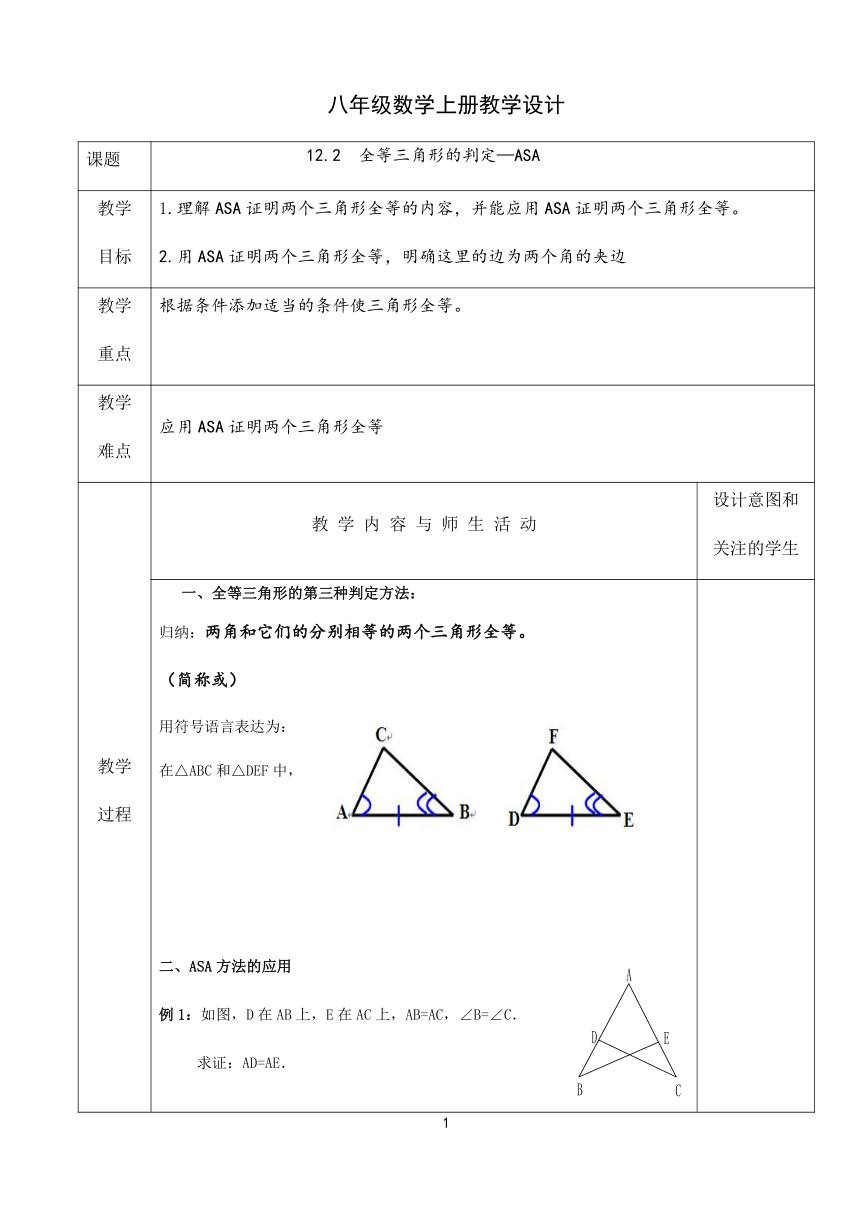
在△ABC和△DEF中,
二、ASA方法的应用
例1:如图,D在AB上,E在AC上,AB=AC,∠B=∠C.
求证:AD=AE.
例2:如图,DE=FE,FC∥AB,
求证:AE=CE
课堂练习
1、为测池塘两岸的两点A、B的距离,在AB的垂线BF上作BC=DC,
再过D作DE⊥BF,使E与A、C在一
条直线上。测得DE的长就是AB的长,
这是为什么?
2、已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证:(1)AD=AE
(2)
BD
=
CE.
2.
已知:如图
,
∠1=∠2
,
∠3=∠4,求证:AC=AB.
3.已知:如图,点B,C,E,F在一条直线上,∠A=∠D,
∠ABC=∠DEF,BE=CF,求证:△ABC≌△DEF
4.
已知:如图,∠A=∠D,
AB∥DE,BE=CF,求证:△ABC≌△DEF
5.
如图,CD与AB相交与点O,AO=BO
,AC∥BD,求证:△AOC≌△BOD。
6.
如图:
AO=BO,OC为∠AOB的角平分线,求证:△AOC≌△BOC
板
书
设
计
教
学
反
思
1
课题
12.2
全等三角形的判定—ASA
教学
目标
1.理解ASA证明两个三角形全等的内容,并能应用ASA证明两个三角形全等。
2.用ASA证明两个三角形全等,明确这里的边为两个角的夹边
教学
重点
根据条件添加适当的条件使三角形全等。
教学
难点
应用ASA证明两个三角形全等
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、全等三角形的第三种判定方法:
归纳:两角和它们的分别相等的两个三角形全等。
(简称或)
用符号语言表达为:
在△ABC和△DEF中,
二、ASA方法的应用
例1:如图,D在AB上,E在AC上,AB=AC,∠B=∠C.
求证:AD=AE.
例2:如图,DE=FE,FC∥AB,
求证:AE=CE
课堂练习
1、为测池塘两岸的两点A、B的距离,在AB的垂线BF上作BC=DC,
再过D作DE⊥BF,使E与A、C在一
条直线上。测得DE的长就是AB的长,
这是为什么?
2、已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证:(1)AD=AE
(2)
BD
=
CE.
2.
已知:如图
,
∠1=∠2
,
∠3=∠4,求证:AC=AB.
3.已知:如图,点B,C,E,F在一条直线上,∠A=∠D,
∠ABC=∠DEF,BE=CF,求证:△ABC≌△DEF
4.
已知:如图,∠A=∠D,
AB∥DE,BE=CF,求证:△ABC≌△DEF
5.
如图,CD与AB相交与点O,AO=BO
,AC∥BD,求证:△AOC≌△BOD。
6.
如图:
AO=BO,OC为∠AOB的角平分线,求证:△AOC≌△BOC
板
书
设
计
教
学
反
思
1
