沪科版七年级数学下学期:第9章分式复习课件(共17张PPT)
文档属性
| 名称 | 沪科版七年级数学下学期:第9章分式复习课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 802.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
分式的概念、性质
分式方程及其应用
分式的乘除、加减
1.分式的定义:
2.分式有意义的条件:
B≠0
分式无意义的条件:
B
=
0
3.分式值为
0
的条件:
A=0且
B
≠0
A
B
形如
,其中
A
,B
都是整式,
且
B
中含有字母.
分式的概念
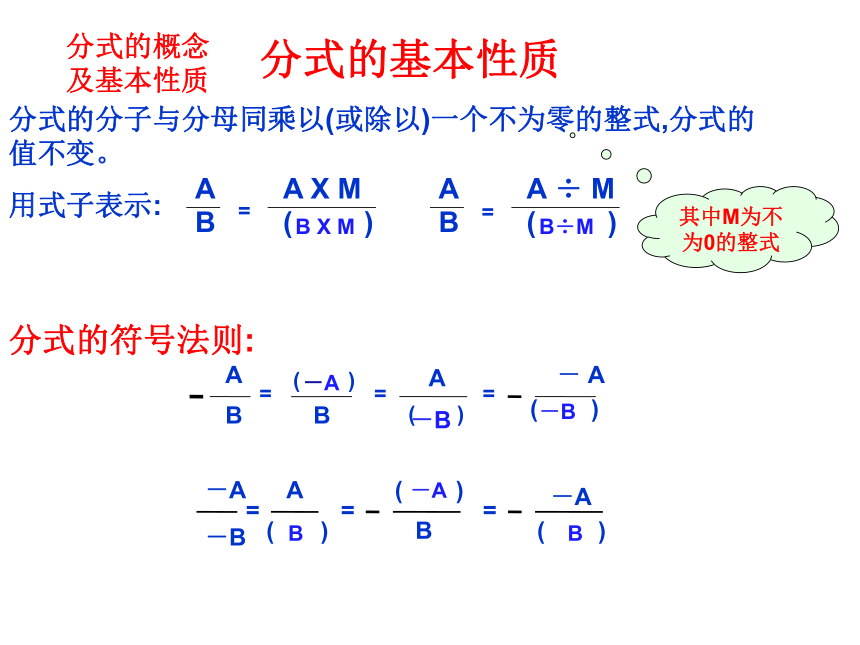
分式的概念及基本性质
分式的基本性质
分式的分子与分母同乘以(或除以)一个不为零的整式,分式的值不变。
用式子表示:
A
B
A
X
M
(
)
A
B
A
÷
M
(
)
=
=
分式的符号法则:
A
B
=
B
(
)
=
A
(
)
=
-
A
(
)
-A
-B
=
A
(
)
=
B
(
)
=
-A
(
)
B
X
M
B÷M
-A
-B
-B
B
-A
B
分式的概念及基本性质
其中M为不为0的整式
分式的乘除法法则
分式乘分式
分式除以分式
分式的乘方
分式的加减
1.同分母分式相加减
2.异分母分式加减时需化为同分母分式加减.
这个相同的分母叫公分母.
(确定公分母的方法:一般取各分母系数的最小公倍数与各分母各个因式的最高次幂的积为公分母)
分式乘除及
加
减
2.当
_________
时,则分式
有意义
3.若分式
的值等于零,则应满
足的条件是
4、写出下列各式中未知的分子或分母:
1.在代数式
中,分式共有_____个。
3
X=2
为常数
保证分母有意义
x≠3且x
≠-3
a2+ab
5、不改变分式的值,使下列分式的分子与分母的最高次项的系数是正数:
6、不改变分式的值,使下列各式分子与分母中各项的系数化为整数:
7.化简:
= .
8.计算:
= .
9.计算:
= .
10.分式
的最简公分
母是_______________
1
11、
,
则
A=_____,B=____.
12、若关于x的方程
产生增根,
则m=______.
13、将公式
变形成用
表示
,则
=
。
14.已知
,那么分式
的值等于
________
2
1
2
3
2、下列分式是最简分式的是
(
)
(A)
(B)
(C)
(D)
C
C
1.下列变形正确的是
(
)
A
B
C
D
3、如果把分式
中的
和
都扩大5倍,
那么这个分式的值
(
)
A.扩大为原来的5倍
B.
不变
C.缩小到原来的
D.扩大到原来的25倍
xy
B
A
5.
化简:
=(
)
A.
1
B.xy
C.
D.
C
6.
化简
的结果是(
)
A.
B.
C.
D.
B
7.
下列各式中,正确的是(
)
A.
B.
C.
D.
D
4、下列各分式中,与
分式的值相等的是(
)
A.
B.
C.
D.
C
例2.请将下面的代数式尽可能化简,再选择一个你
喜欢的数代入求值
乘除为同级运算,运算顺序从左到右
错误!!!
例2.请将下面的代数式尽可能化简,再选择一个你
喜欢的数代入求值
a的取值保证分式有意义
1.
化简:
解:原式=
2.
化简:
解:原式
3.
先化简,再求值:
÷
其中a满足
a-1
a+2
-
a
2
-4
a
2
-2a+1
1
a
2
-1
4.
先化简
÷
然后对a取一个你喜欢的数代入求值.
5.
有一道题“先化简,再求值:
,其中x=-3”
。小玲做题时
把“x=-3”错抄成了“x=3”,但她的计算结果也是正确的,请你解释这是怎么回事?
÷
6.
计算
÷
的值,其中x=2006。
某同学把“x=2006”错抄成“x=2060”,但他的计算结果是正确的,请回答这是怎么回事?试说明理由。
x
-4
(
x+1
2
-
2
x+2
)
x-5
x+2
x
(2-x)
经检验,
分式方程必须检验,若有增根,要舍去
分式方程
及其应用
找出公分母
分式方程及其应用
阿姨,我买些梨.
从这段对话里得出哪些信息或等量关系?
是小红啊!
你上次买的那种梨都卖完了,我们还没来
得及进货,我建议你这次买些新进的苹果,不过价格
要比梨贵一点,每千克苹果的价格是梨的1.5倍.
好吧,这次照上次一样,也花30元钱.
哟,巧了!这次苹果的质量正好比上次梨的质量轻2.5千克.
对啊,我本来就想要考考你,你能算出我这里的梨和苹果
的单价么?
-
-
-
过了一会儿,苹果称好了
-
-
-
例2.请看下面一段对话:
请同学们帮帮小红吧!
小
红:
售货员:
小
红:
小
红:
售货员:
分式的概念、性质
分式方程及其应用
分式的乘除、加减
1.分式的定义:
2.分式有意义的条件:
B≠0
分式无意义的条件:
B
=
0
3.分式值为
0
的条件:
A=0且
B
≠0
A
B
形如
,其中
A
,B
都是整式,
且
B
中含有字母.
分式的概念
分式的概念及基本性质
分式的基本性质
分式的分子与分母同乘以(或除以)一个不为零的整式,分式的值不变。
用式子表示:
A
B
A
X
M
(
)
A
B
A
÷
M
(
)
=
=
分式的符号法则:
A
B
=
B
(
)
=
A
(
)
=
-
A
(
)
-A
-B
=
A
(
)
=
B
(
)
=
-A
(
)
B
X
M
B÷M
-A
-B
-B
B
-A
B
分式的概念及基本性质
其中M为不为0的整式
分式的乘除法法则
分式乘分式
分式除以分式
分式的乘方
分式的加减
1.同分母分式相加减
2.异分母分式加减时需化为同分母分式加减.
这个相同的分母叫公分母.
(确定公分母的方法:一般取各分母系数的最小公倍数与各分母各个因式的最高次幂的积为公分母)
分式乘除及
加
减
2.当
_________
时,则分式
有意义
3.若分式
的值等于零,则应满
足的条件是
4、写出下列各式中未知的分子或分母:
1.在代数式
中,分式共有_____个。
3
X=2
为常数
保证分母有意义
x≠3且x
≠-3
a2+ab
5、不改变分式的值,使下列分式的分子与分母的最高次项的系数是正数:
6、不改变分式的值,使下列各式分子与分母中各项的系数化为整数:
7.化简:
= .
8.计算:
= .
9.计算:
= .
10.分式
的最简公分
母是_______________
1
11、
,
则
A=_____,B=____.
12、若关于x的方程
产生增根,
则m=______.
13、将公式
变形成用
表示
,则
=
。
14.已知
,那么分式
的值等于
________
2
1
2
3
2、下列分式是最简分式的是
(
)
(A)
(B)
(C)
(D)
C
C
1.下列变形正确的是
(
)
A
B
C
D
3、如果把分式
中的
和
都扩大5倍,
那么这个分式的值
(
)
A.扩大为原来的5倍
B.
不变
C.缩小到原来的
D.扩大到原来的25倍
xy
B
A
5.
化简:
=(
)
A.
1
B.xy
C.
D.
C
6.
化简
的结果是(
)
A.
B.
C.
D.
B
7.
下列各式中,正确的是(
)
A.
B.
C.
D.
D
4、下列各分式中,与
分式的值相等的是(
)
A.
B.
C.
D.
C
例2.请将下面的代数式尽可能化简,再选择一个你
喜欢的数代入求值
乘除为同级运算,运算顺序从左到右
错误!!!
例2.请将下面的代数式尽可能化简,再选择一个你
喜欢的数代入求值
a的取值保证分式有意义
1.
化简:
解:原式=
2.
化简:
解:原式
3.
先化简,再求值:
÷
其中a满足
a-1
a+2
-
a
2
-4
a
2
-2a+1
1
a
2
-1
4.
先化简
÷
然后对a取一个你喜欢的数代入求值.
5.
有一道题“先化简,再求值:
,其中x=-3”
。小玲做题时
把“x=-3”错抄成了“x=3”,但她的计算结果也是正确的,请你解释这是怎么回事?
÷
6.
计算
÷
的值,其中x=2006。
某同学把“x=2006”错抄成“x=2060”,但他的计算结果是正确的,请回答这是怎么回事?试说明理由。
x
-4
(
x+1
2
-
2
x+2
)
x-5
x+2
x
(2-x)
经检验,
分式方程必须检验,若有增根,要舍去
分式方程
及其应用
找出公分母
分式方程及其应用
阿姨,我买些梨.
从这段对话里得出哪些信息或等量关系?
是小红啊!
你上次买的那种梨都卖完了,我们还没来
得及进货,我建议你这次买些新进的苹果,不过价格
要比梨贵一点,每千克苹果的价格是梨的1.5倍.
好吧,这次照上次一样,也花30元钱.
哟,巧了!这次苹果的质量正好比上次梨的质量轻2.5千克.
对啊,我本来就想要考考你,你能算出我这里的梨和苹果
的单价么?
-
-
-
过了一会儿,苹果称好了
-
-
-
例2.请看下面一段对话:
请同学们帮帮小红吧!
小
红:
售货员:
小
红:
小
红:
售货员:
