五年级下册数学教案-1.3 面积的估测(二) 沪教版
文档属性
| 名称 | 五年级下册数学教案-1.3 面积的估测(二) 沪教版 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 00:00:00 | ||
图片预览

文档简介
面积的估测
教学内容:课本第6、7页
教学目标:
1、初步掌握“通过将图形近似地看作可求面积的多边形对图形的面积进行估测”的方法。
2、会用数格子方法和近似图形求积法估测不规则图形的面积。
3、在想想、画画、算算的过程中激发学生学习数学的兴趣,培养学生的语言表达能力和合作探究精神,发展学生思维的灵活性。
教学重点:选择合适的面积公式进行计算。
教学难点:从规则的简单图形到近似的不规则图形之间建立联系。学生能体会用不同的方法去估测一个不规则图形的面积,而方法的不同可能引起估测结果的不同。
教学过程:
复习引入
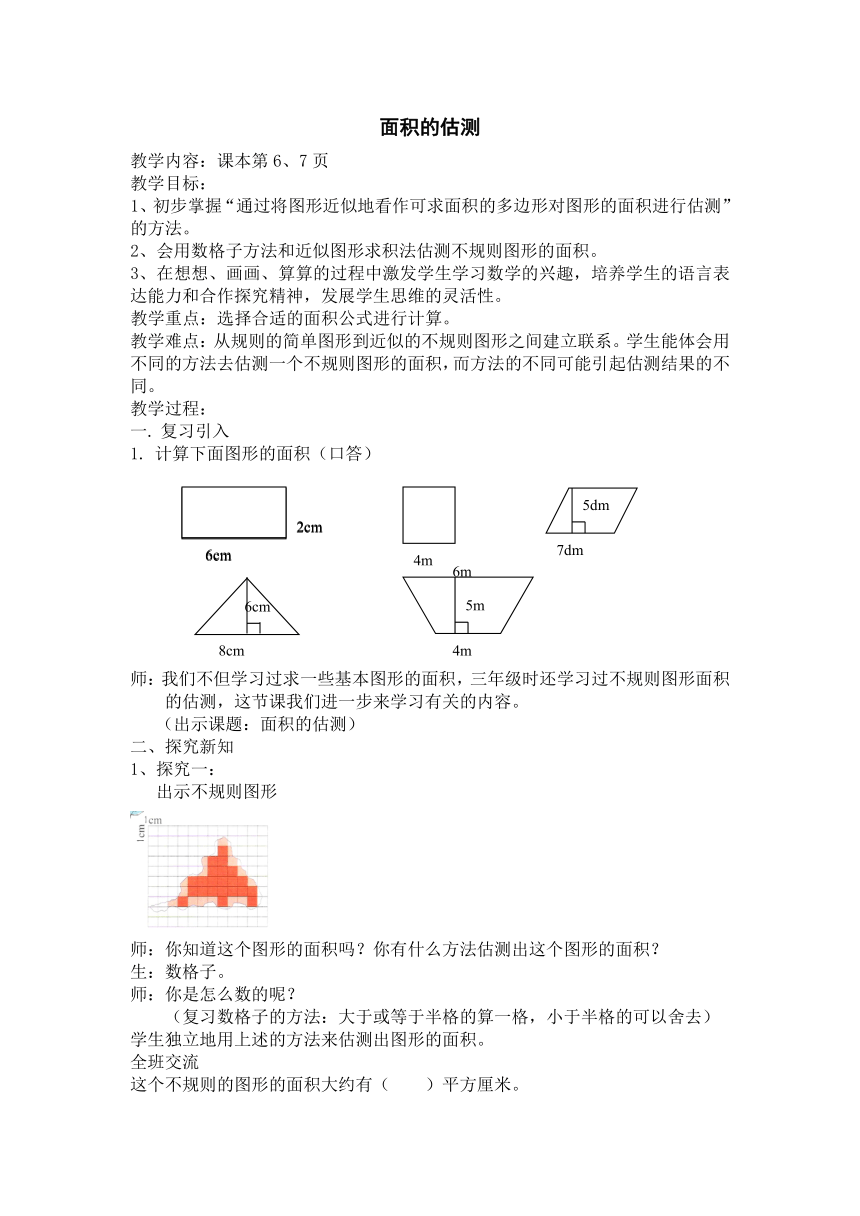
计算下面图形的面积(口答)
师:我们不但学习过求一些基本图形的面积,三年级时还学习过不规则图形面积的估测,这节课我们进一步来学习有关的内容。
(出示课题:面积的估测)
二、探究新知
1、探究一:
出示不规则图形
师:你知道这个图形的面积吗?你有什么方法估测出这个图形的面积?
生:数格子。
师:你是怎么数的呢?
(复习数格子的方法:大于或等于半格的算一格,小于半格的可以舍去)
学生独立地用上述的方法来估测出图形的面积。
全班交流
这个不规则的图形的面积大约有( )平方厘米。
师:还可以用什么方法估测出这个不规则图形的面积呢?
探究二:
利用已学的面积公式来估测面积
(1)观察图形,想象这个图形的形状特点
提问:这个图形和哪个我们知道的平面图形很相似?
回答:三角形。
师:那你们能不能自己动手画一画这个三角形?
尝试根据不规则图形的大小画出合适大小的三角形。
要求:学生根据计算需要画出合适的三角形。
出示三种不同的画法:三角形的大小合适;
三角形的面积比不规则图形的面积大;
三角形的面积比不规则图形的面积小。
提问:大家来看看这些同学画出的三角形有什么不同?
你认为哪种情况比较合理呢?
回答:在将图形近似地看作可求面积的多边形对图形的面积进行估测的候,也要根据图形的大小合理画出近似的基本图形。
2、提问:确定了合理的三角形后能利用三角形的面积计算公式来估测这个图形的大小吗?
回答:利用格子图找出三角形的底和高就能估测出这个图形的大小了
3、用上述的方法计算出图形的面积
S=ah÷2 10×7÷2=35(㎝2)
这个三角形的面积是( 35 )平方厘米。
这个图形的面积大约是( 35 )平方厘米。
出示:2种估测的结果
提问:用两种不同的方法估测出的答案不一致。为什么会出现这样的情况?
回答:因为是估测,误差是允许的,但不能过大。
巩固练习
练习一:
判断:
练习二:动手画一画,并选择一幅估测出它的面积
探究三:估测下列图形的面积
提问:这个不规则图形可以把它近似的看成什么基本图形呢?
回答:平行四边形。
提问:盖上格子图能不能求出它的面积呢?
回答:不能。通过格子图不能知道梯形的上底、下底和高。
提问:那怎么估测出这个图形的面积呢?
回答:可以把图形看成两个三角形来计算出近似面积。
3、小结:刚才的这两种方法都可以用来估测不规则图形的面积。既可以根据格子图来估测不规则图形的大小,也可以把不规则图形近似地看作可求面积的多边形,从而对不规则图形的面积进行估测。——这就是今天我们学习的面积估测方法。
总结:
问:通过今天的学习你有什么可以告诉大家的呢?
教学内容:课本第6、7页
教学目标:
1、初步掌握“通过将图形近似地看作可求面积的多边形对图形的面积进行估测”的方法。
2、会用数格子方法和近似图形求积法估测不规则图形的面积。
3、在想想、画画、算算的过程中激发学生学习数学的兴趣,培养学生的语言表达能力和合作探究精神,发展学生思维的灵活性。
教学重点:选择合适的面积公式进行计算。
教学难点:从规则的简单图形到近似的不规则图形之间建立联系。学生能体会用不同的方法去估测一个不规则图形的面积,而方法的不同可能引起估测结果的不同。
教学过程:
复习引入
计算下面图形的面积(口答)
师:我们不但学习过求一些基本图形的面积,三年级时还学习过不规则图形面积的估测,这节课我们进一步来学习有关的内容。
(出示课题:面积的估测)
二、探究新知
1、探究一:
出示不规则图形
师:你知道这个图形的面积吗?你有什么方法估测出这个图形的面积?
生:数格子。
师:你是怎么数的呢?
(复习数格子的方法:大于或等于半格的算一格,小于半格的可以舍去)
学生独立地用上述的方法来估测出图形的面积。
全班交流
这个不规则的图形的面积大约有( )平方厘米。
师:还可以用什么方法估测出这个不规则图形的面积呢?
探究二:
利用已学的面积公式来估测面积
(1)观察图形,想象这个图形的形状特点
提问:这个图形和哪个我们知道的平面图形很相似?
回答:三角形。
师:那你们能不能自己动手画一画这个三角形?
尝试根据不规则图形的大小画出合适大小的三角形。
要求:学生根据计算需要画出合适的三角形。
出示三种不同的画法:三角形的大小合适;
三角形的面积比不规则图形的面积大;
三角形的面积比不规则图形的面积小。
提问:大家来看看这些同学画出的三角形有什么不同?
你认为哪种情况比较合理呢?
回答:在将图形近似地看作可求面积的多边形对图形的面积进行估测的候,也要根据图形的大小合理画出近似的基本图形。
2、提问:确定了合理的三角形后能利用三角形的面积计算公式来估测这个图形的大小吗?
回答:利用格子图找出三角形的底和高就能估测出这个图形的大小了
3、用上述的方法计算出图形的面积
S=ah÷2 10×7÷2=35(㎝2)
这个三角形的面积是( 35 )平方厘米。
这个图形的面积大约是( 35 )平方厘米。
出示:2种估测的结果
提问:用两种不同的方法估测出的答案不一致。为什么会出现这样的情况?
回答:因为是估测,误差是允许的,但不能过大。
巩固练习
练习一:
判断:
练习二:动手画一画,并选择一幅估测出它的面积
探究三:估测下列图形的面积
提问:这个不规则图形可以把它近似的看成什么基本图形呢?
回答:平行四边形。
提问:盖上格子图能不能求出它的面积呢?
回答:不能。通过格子图不能知道梯形的上底、下底和高。
提问:那怎么估测出这个图形的面积呢?
回答:可以把图形看成两个三角形来计算出近似面积。
3、小结:刚才的这两种方法都可以用来估测不规则图形的面积。既可以根据格子图来估测不规则图形的大小,也可以把不规则图形近似地看作可求面积的多边形,从而对不规则图形的面积进行估测。——这就是今天我们学习的面积估测方法。
总结:
问:通过今天的学习你有什么可以告诉大家的呢?
