吉林省长春市第八中学2020-2021学年高一上学期数学期末复习1(12月) Word版含答案解析
文档属性
| 名称 | 吉林省长春市第八中学2020-2021学年高一上学期数学期末复习1(12月) Word版含答案解析 |  | |
| 格式 | docx | ||
| 文件大小 | 644.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 13:21:07 | ||
图片预览




文档简介
长春市第八中学2020-2021学年高一上学期数学期末复习1
一、单选题
1.下列各组中的false,false表示同一集合的是( )
A.false,false
B.false,false
C.false,false
D.false,false
2.若false是第四象限的角,则false所在象限是( )
A.第一象限 B.第二象限
C.第一或第二象限 D.第二或第四象限
3.已知false,则下列不等式成立的是( )
A.false B.false
C.false D.false
4.已知方程false的两根为false,false,则false( )
A.false B.false C.false D.false
5.下列函数中哪个与函数y=x相等( )
A.y=()2 B.y C.y D.y
6.若false,则false( )
A.false B.false C.false D.false
7.下列命题中,真命题是( )
A.false,false B.false,false
C.若false,false,则false D.false是false的充分不必要条件
8.设false,则false的最小值是( )
A.false B.false C.false D.false
9.已知false,且满足false,则false( )
A.false B.1 C.false D.false
10.已知函数false,其中false表示不大于x的最大整数(如false,false),则函数false的零点个数是( )
A.1 B.2 C.3 D.4
二、多选题
11.设false、false和false分别是角false的正弦、余弦和正切线,则以下不等式正确的是( )
A.false B.false
C.false D.false
12.具有性质:false的函数,我们称为满足“倒负”变换的了函数下列函数中了函数有( )
A.false B.falseC.falseD.false
三、填空题
13.设函数false,则false _________.
14.已知集合U={1,2,3,4,5},A={1,2},B={3,4},则false
15.已知false,则false_______________.
16.设函数false的图象关于直线false对称,它的周期为false,则下列说法正确是________(填写序号)
①false的图象过点false;
②false在false上单调递减;
③false的一个对称中心是false;
④将false的图象向右平移false个单位长度得到函数false的图象.
四、解答题
17.试判断“false”是“false”的什么条件.
18.已知函数false,求:
(1)false;
(2)false.
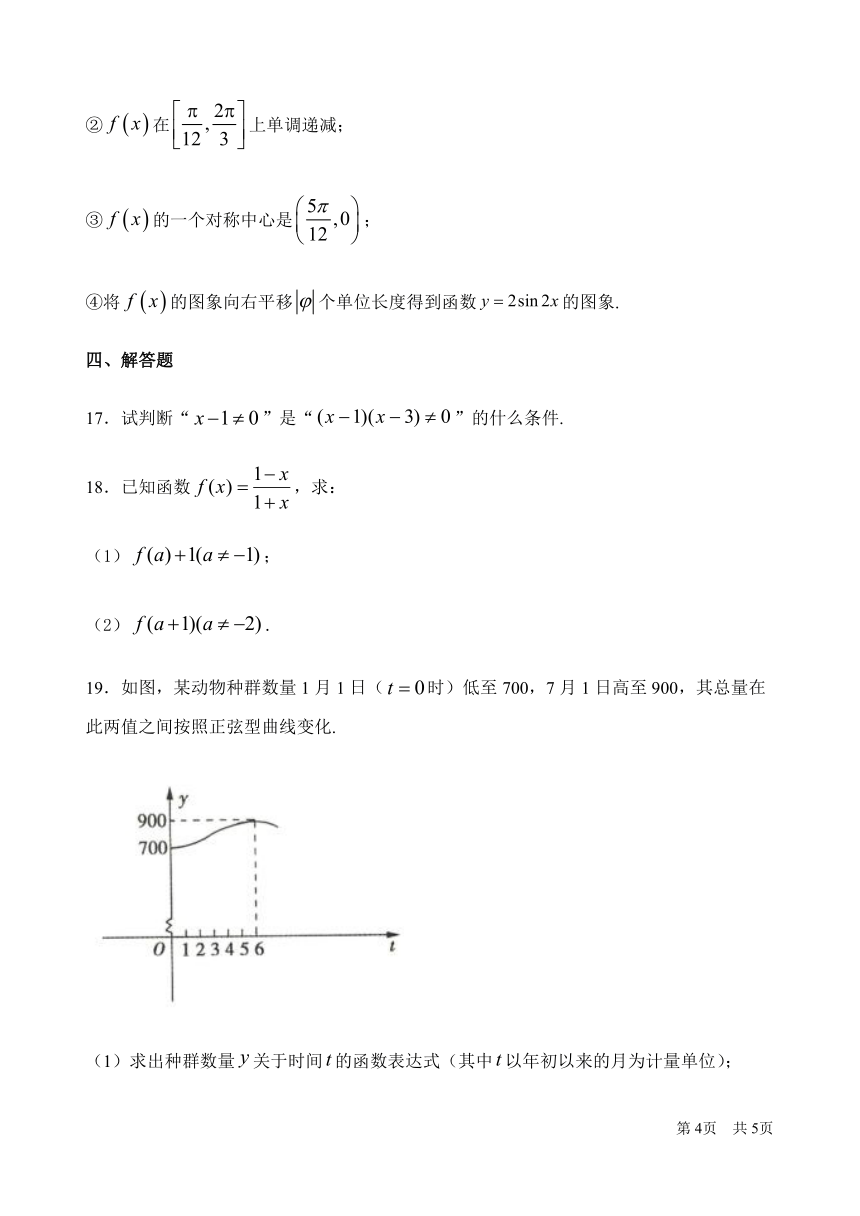
19.如图,某动物种群数量1月1日(false时)低至700,7月1日高至900,其总量在此两值之间按照正弦型曲线变化.
(1)求出种群数量false关于时间false的函数表达式(其中false以年初以来的月为计量单位);
(2)估计当年3月1日动物种群数量.
20.已知函数false.
(1)求false的最小正周期,并求false的最小值及取得最小值时false的集合;
(2)令false,若false对于false恒成立,求实数false的取值范围.
21.已知函数false为奇函数.
(1)求实数false的值;
(2)判断并证明函数false的单调性;
(3)若存在false,使得函数false在区间false上的值域为false,求实数false的取值范围.
参考答案
1.D
【分析】
根据集合相等的概念依次分析各选项即可得答案.
【详解】
解:对于A选项,false有两个实数元素,false表示点false,故不正确;
对于B选项,false表示点false,false表示点false,故不正确;
对于C选项,false表示函数false的值域,false表示函数false图象上的所有点的集合,故不正确;
对于D选项,均表示函数false的值域,故正确.
故选:D.
【点睛】
本题考查集合相等的概念,是基础题.
2.D
【解析】
【分析】
表示出false在第四象限的集合,再求false所在象限的集合即可
【详解】
由题可知false,故false,故false所在象限是第二或第四象限
故选D
【点睛】
本题考查false所在象限的判断,常规思路为:先表示出false所在象限集合,再求false对应集合,结合具体false值综合分析
3.C
【分析】
根据不等式的性质逐个判断可得答案.
【详解】
由false得false,false不正确;
由false得false,所以false,即false,false不正确;
由false得false,false正确;
由false得false,所以false,即false,false不正确.
故选:C
【点睛】
关键点点睛:熟练掌握不等式的性质是解决此题的关键,属于基础题.
4.C
【分析】
对方程false分解为false,可求出false,false,即可求出false的值.
【详解】
将原方程因式分解为false,所以false或 false,所以false或false,所以falsefalse.故选C.
【点睛】
本题主要考查了对数的运算,属于基础题.
5.C
【解析】
【分析】
可看出y=x的定义域为R,通过求定义域可得出选项A,B的两函数的定义域和y=x的定义域都不相同,从而判断A,B都错误.而通过化简选项D的函数解析式,可得出D的解析式和y=x不同,从而判断D也错误,只能选C.
【详解】
y=x的定义域为R;
A.的定义域为{x|x≥0},定义域不同,与y=x不相等;
B.的定义域为{x|x≠0},定义域不同,不相等;
C.的定义域为R,且解析式相同,与y=x相等;
D.,解析式不同,不相等.
故选:C.
【点睛】
本题考查函数的定义,判断两函数是否相等的方法:定义域和解析式是否都相同.
6.B
【分析】
由分数指数幂的运算性质,结合false,false运算即可得解.
【详解】
解:false,false,false,false,false,
故选:B..
【点睛】
本题考查了分数指数幂的运算,重点考查了运算能力,属基础题.
7.D
【分析】
对选项进行逐个分析即得。
【详解】
当false时,false,故A错误;由指数函数的性质可知,故B错误;根据同向可加性只能得出false,故C错误;false可得false,反之不成立,故D正确.
故选:D
【点睛】
本题考查判断真命题,是基础题。
8.B
【分析】
先把代数式false整理成false,然后利用基本不等式可求出原式的最小值.
【详解】
falsefalse,当且仅当false时,即当false,false,false时,等号成立,
因此,false的最小值是false.
故选:B.
【点睛】
本题考查利用基本不等式求代数式的最小值,解题的关键就是要对代数式进行合理配凑,考查计算能力,属于中等题.
9.B
【分析】
对代数式变形左侧false,化简即可求得false,对所求代数式变形false,即可得解.
【详解】
∵false,
∴false
false
false,
∴false,把false代入,得原式false.
故选:B
【点睛】
此题考查同角三角函数基本关系,根据三角变换化简求值,构造齐次式求代数式的值.
10.D
【分析】
构造函数false与false,作出图象,结合图象得出两函数的交点个数,即可求解.
【详解】
设函数false,false,
则false,所以函数false为定义域上的为偶函数,
作出函数false与false的图象,如图所示,
当false时,false,结合图象,两函数有1个交点,即1个零点;
当false时,false,结合图象,两函数有1个交点,即1个零点;
当false时,false,两函数有1个交点,即1个零点;
当false时,false,false,此时两函数有1个交点,即1个零点,综上可得函数false共4个零点.
故选:D.
【点睛】
本题主要考查了函数的零点个数的判定,以及函数的图象的应用,其中解答中构造新函数,作出函数的图象,结合两个函数的图象的交点个数进行判定是解答的关键,着重考查构造思想,以及数形结合思想的应用,属于中档试题.
11.BC
【分析】
作出角false的正弦、余弦和正切线,根据三角函数线定义,即可得出结果.
【详解】
分别作角false的正弦、余弦和正切线,如图,
false.
false.
故选:BC.
【点睛】
本题考查利用三角函数线比较同角三角函数值的大小比较,考查数形结合思想的应用,难度较易.
12.AC
【分析】
根据所给的倒负变换的定义逐一判断即可.
【详解】
选项A:false,所以函数false符合题意;
选项B:false,所以函数false不符合题意;
选项C:当false时,false,所以有false,
当false时,false,
当false时,false,所以有false,所以函数false符合题意;
选项D:falsefalse,所以不符合题意.
故选:AC
【点睛】
考查了新定义题,考查了数学运算能力.
13.15
【分析】
先求内层函数值,再求外层函数值即可,
【详解】
∵函数false,∴false,false.
故答案为:15
【点睛】
本题考查由分段函数求解函数值,属于基础题
14.false
【解析】
解:因为集合U={1,2,3,4,5},A={1,2},B={3,4},false
15.false
【解析】
【分析】
注意到false的关系,运用角度变换,将false改写为false,运用诱导公式,转化为求false,结合同角三角函数关系,即可。
【详解】
false=false
=false
=false
=false
=false
【点睛】
本题考查诱导公式及同角三角函数关系,属于基础题。本题关键是通过角度变换,将false改写为false,及巧妙运用同角三角函数关系式。
16.③
【分析】
先根据对称轴及最小正周期,求得函数false的解析式.再结合正弦函数的图象与性质,判断点是否在函数图象上,求得函数的单调区间及对称中心判断选项,由平移变换求得变化后的解析式并对比即可.
【详解】
函数false的最小正周期是false,所以false,则false,
又false图象关于直线false对称,
所以对称轴为false,代入可得false,解得false,
因为false,所以当false时, false,则false,
对于①,当false时,false,false的图象不过点false,所以①不正确;
对于②,false的单调递减区间为false,解得false,
当false时,false,又因为false,则false在false上不是减函数,所以②错误;
对于③,false的对称中心为false,解得false,当false时,false,所以false是false的一个对称中心,所以③正确;
对于④,将false向右平移false个单位长度,可得false,所以不能得到false的图象,所以④错误.
综上可知,正确的为③.
故答案为: ③.
【点睛】
本题考查了三角函数解析式的求法,正弦函数的图像与性质的综合应用,属于中档题.
17.必要非充分条件
【分析】
利用等价命题的转化,再根据充分条件,必要条件的定义即可判断.
【详解】
当false时,有false,可知false;
当false时,一定有false,故false,
即“false”是“false”的必要条件.
又当false时,取false,可得false.所以false.
因此,“false”是“false”的必要非充分条件.
【点睛】
本题考查原命题与逆否命题为等价命题,考查充分、必要条件,属于基础题.
18.(1)false
(2)false.
【分析】
(1)直接代入数据化简得到答案.
(2)直接代入数据化简得到答案.
【详解】
(1)false
(2)false.
【点睛】
本题考查了求函数表达式,属于简单题.
19.(1)false; (2)当年3月1日动物种群数量约是750.
【分析】
(1)首先设种群数量false关于false的解析式为false,然后根据图象上最大值和最小值求false和false,根据周期求false,最后代入false ,false求false,得到函数的解析式;(2)3月1日是false ,根据(1)的解析式,求false时的函数值.
【详解】
(1)设种群数量false关于false的解析式为false,
则false,解得false.
又周期false,false,
false.
又当false时,false,
false,false,
false,false可取false,false.
(2)当false时,false,
即当年3月1日动物种群数量约是750.
【点睛】
本题考查根据函数的图象求三角函数的解析式,意在考查分析和整理数据,抽象和概括能力,属于中档题型.
20.(1)最小正周期是false,最小值为false.false的集合为false;
(2)false.
【分析】
(1)化简函数false,结合三角函数的图象与性质,即可求解;
(2)化简false,根据false,求得false的最大值为false,再根据题意,得到false,即可求解.
【详解】
(1)由题意,函数false,
可得其最小正周期是false,
当false,可得false,即false时,
函数false的最小值为false.
此时false的集合为false.
(2)由false
因为false,得false,则false,
所以false,
若false对于false恒成立,则false,
所以false,即求实数false的取值范围false.
【点睛】
本题主要考查了三角恒等变换,以及三角函数的图象与性质综合应用,其中解答中利用三角恒等变换的公式,求得函数的解析式,结合三角函数的图象与性质求解是解答的关键,着重考查了推理与运算能力,属于中档试题.
21.(1)1;(2)增函数,证明见解析;(3)false
【分析】
(1)根据函数奇函数的定义和条件false,求出k的值之后再验证是否满足函数的定义域关于原点对称即可;
(2)根据函数的单调性和对数函数的单调性即可证明;
(3)假设存在false,使得函数false在区间false上的值域为false,由false 在false上递增,程false在false上有两个不等实根,可得false的不等式组,解不等式即可得到实数false的取值范围,即可得到判断存在性.
【详解】
(1)因为函数false为奇函数,所以false,
即false对定义域内任意false恒成立,所以false,即false,
显然false,又当false时,false的定义域关于原点对称.
所以false为满足题意的值.
(2)结论:false在false,false上均为增函数.
证明:由(1)知false,其定义域为false,
任取false,不妨设false,则
false,
因为false,又false,
所以false,所以false,
即false,所以false在false上为增函数.
同理,false在false上为增函数.
(3)由(2)知false在false上为增函数,
又因为函数false在false上的值域为false,
所以false,且false,所以false,
即false是方程false的两实根,
问题等价于方程false在false上有两个不等实根,
令false,对称轴false
则false,
即false,解得false.
【点睛】
本题主要考查函数奇偶性和单调性的应用以及函数和方程的转化以及一元二次方程在给定区间上解的问题,根据函数奇偶性和单调性的定义函数性质是解决本题的关键,考查学生分析问题与解决问题的能力,是难题.
一、单选题
1.下列各组中的false,false表示同一集合的是( )
A.false,false
B.false,false
C.false,false
D.false,false
2.若false是第四象限的角,则false所在象限是( )
A.第一象限 B.第二象限
C.第一或第二象限 D.第二或第四象限
3.已知false,则下列不等式成立的是( )
A.false B.false
C.false D.false
4.已知方程false的两根为false,false,则false( )
A.false B.false C.false D.false
5.下列函数中哪个与函数y=x相等( )
A.y=()2 B.y C.y D.y
6.若false,则false( )
A.false B.false C.false D.false
7.下列命题中,真命题是( )
A.false,false B.false,false
C.若false,false,则false D.false是false的充分不必要条件
8.设false,则false的最小值是( )
A.false B.false C.false D.false
9.已知false,且满足false,则false( )
A.false B.1 C.false D.false
10.已知函数false,其中false表示不大于x的最大整数(如false,false),则函数false的零点个数是( )
A.1 B.2 C.3 D.4
二、多选题
11.设false、false和false分别是角false的正弦、余弦和正切线,则以下不等式正确的是( )
A.false B.false
C.false D.false
12.具有性质:false的函数,我们称为满足“倒负”变换的了函数下列函数中了函数有( )
A.false B.falseC.falseD.false
三、填空题
13.设函数false,则false _________.
14.已知集合U={1,2,3,4,5},A={1,2},B={3,4},则false
15.已知false,则false_______________.
16.设函数false的图象关于直线false对称,它的周期为false,则下列说法正确是________(填写序号)
①false的图象过点false;
②false在false上单调递减;
③false的一个对称中心是false;
④将false的图象向右平移false个单位长度得到函数false的图象.
四、解答题
17.试判断“false”是“false”的什么条件.
18.已知函数false,求:
(1)false;
(2)false.
19.如图,某动物种群数量1月1日(false时)低至700,7月1日高至900,其总量在此两值之间按照正弦型曲线变化.
(1)求出种群数量false关于时间false的函数表达式(其中false以年初以来的月为计量单位);
(2)估计当年3月1日动物种群数量.
20.已知函数false.
(1)求false的最小正周期,并求false的最小值及取得最小值时false的集合;
(2)令false,若false对于false恒成立,求实数false的取值范围.
21.已知函数false为奇函数.
(1)求实数false的值;
(2)判断并证明函数false的单调性;
(3)若存在false,使得函数false在区间false上的值域为false,求实数false的取值范围.
参考答案
1.D
【分析】
根据集合相等的概念依次分析各选项即可得答案.
【详解】
解:对于A选项,false有两个实数元素,false表示点false,故不正确;
对于B选项,false表示点false,false表示点false,故不正确;
对于C选项,false表示函数false的值域,false表示函数false图象上的所有点的集合,故不正确;
对于D选项,均表示函数false的值域,故正确.
故选:D.
【点睛】
本题考查集合相等的概念,是基础题.
2.D
【解析】
【分析】
表示出false在第四象限的集合,再求false所在象限的集合即可
【详解】
由题可知false,故false,故false所在象限是第二或第四象限
故选D
【点睛】
本题考查false所在象限的判断,常规思路为:先表示出false所在象限集合,再求false对应集合,结合具体false值综合分析
3.C
【分析】
根据不等式的性质逐个判断可得答案.
【详解】
由false得false,false不正确;
由false得false,所以false,即false,false不正确;
由false得false,false正确;
由false得false,所以false,即false,false不正确.
故选:C
【点睛】
关键点点睛:熟练掌握不等式的性质是解决此题的关键,属于基础题.
4.C
【分析】
对方程false分解为false,可求出false,false,即可求出false的值.
【详解】
将原方程因式分解为false,所以false或 false,所以false或false,所以falsefalse.故选C.
【点睛】
本题主要考查了对数的运算,属于基础题.
5.C
【解析】
【分析】
可看出y=x的定义域为R,通过求定义域可得出选项A,B的两函数的定义域和y=x的定义域都不相同,从而判断A,B都错误.而通过化简选项D的函数解析式,可得出D的解析式和y=x不同,从而判断D也错误,只能选C.
【详解】
y=x的定义域为R;
A.的定义域为{x|x≥0},定义域不同,与y=x不相等;
B.的定义域为{x|x≠0},定义域不同,不相等;
C.的定义域为R,且解析式相同,与y=x相等;
D.,解析式不同,不相等.
故选:C.
【点睛】
本题考查函数的定义,判断两函数是否相等的方法:定义域和解析式是否都相同.
6.B
【分析】
由分数指数幂的运算性质,结合false,false运算即可得解.
【详解】
解:false,false,false,false,false,
故选:B..
【点睛】
本题考查了分数指数幂的运算,重点考查了运算能力,属基础题.
7.D
【分析】
对选项进行逐个分析即得。
【详解】
当false时,false,故A错误;由指数函数的性质可知,故B错误;根据同向可加性只能得出false,故C错误;false可得false,反之不成立,故D正确.
故选:D
【点睛】
本题考查判断真命题,是基础题。
8.B
【分析】
先把代数式false整理成false,然后利用基本不等式可求出原式的最小值.
【详解】
falsefalse,当且仅当false时,即当false,false,false时,等号成立,
因此,false的最小值是false.
故选:B.
【点睛】
本题考查利用基本不等式求代数式的最小值,解题的关键就是要对代数式进行合理配凑,考查计算能力,属于中等题.
9.B
【分析】
对代数式变形左侧false,化简即可求得false,对所求代数式变形false,即可得解.
【详解】
∵false,
∴false
false
false,
∴false,把false代入,得原式false.
故选:B
【点睛】
此题考查同角三角函数基本关系,根据三角变换化简求值,构造齐次式求代数式的值.
10.D
【分析】
构造函数false与false,作出图象,结合图象得出两函数的交点个数,即可求解.
【详解】
设函数false,false,
则false,所以函数false为定义域上的为偶函数,
作出函数false与false的图象,如图所示,
当false时,false,结合图象,两函数有1个交点,即1个零点;
当false时,false,结合图象,两函数有1个交点,即1个零点;
当false时,false,两函数有1个交点,即1个零点;
当false时,false,false,此时两函数有1个交点,即1个零点,综上可得函数false共4个零点.
故选:D.
【点睛】
本题主要考查了函数的零点个数的判定,以及函数的图象的应用,其中解答中构造新函数,作出函数的图象,结合两个函数的图象的交点个数进行判定是解答的关键,着重考查构造思想,以及数形结合思想的应用,属于中档试题.
11.BC
【分析】
作出角false的正弦、余弦和正切线,根据三角函数线定义,即可得出结果.
【详解】
分别作角false的正弦、余弦和正切线,如图,
false.
false.
故选:BC.
【点睛】
本题考查利用三角函数线比较同角三角函数值的大小比较,考查数形结合思想的应用,难度较易.
12.AC
【分析】
根据所给的倒负变换的定义逐一判断即可.
【详解】
选项A:false,所以函数false符合题意;
选项B:false,所以函数false不符合题意;
选项C:当false时,false,所以有false,
当false时,false,
当false时,false,所以有false,所以函数false符合题意;
选项D:falsefalse,所以不符合题意.
故选:AC
【点睛】
考查了新定义题,考查了数学运算能力.
13.15
【分析】
先求内层函数值,再求外层函数值即可,
【详解】
∵函数false,∴false,false.
故答案为:15
【点睛】
本题考查由分段函数求解函数值,属于基础题
14.false
【解析】
解:因为集合U={1,2,3,4,5},A={1,2},B={3,4},false
15.false
【解析】
【分析】
注意到false的关系,运用角度变换,将false改写为false,运用诱导公式,转化为求false,结合同角三角函数关系,即可。
【详解】
false=false
=false
=false
=false
=false
【点睛】
本题考查诱导公式及同角三角函数关系,属于基础题。本题关键是通过角度变换,将false改写为false,及巧妙运用同角三角函数关系式。
16.③
【分析】
先根据对称轴及最小正周期,求得函数false的解析式.再结合正弦函数的图象与性质,判断点是否在函数图象上,求得函数的单调区间及对称中心判断选项,由平移变换求得变化后的解析式并对比即可.
【详解】
函数false的最小正周期是false,所以false,则false,
又false图象关于直线false对称,
所以对称轴为false,代入可得false,解得false,
因为false,所以当false时, false,则false,
对于①,当false时,false,false的图象不过点false,所以①不正确;
对于②,false的单调递减区间为false,解得false,
当false时,false,又因为false,则false在false上不是减函数,所以②错误;
对于③,false的对称中心为false,解得false,当false时,false,所以false是false的一个对称中心,所以③正确;
对于④,将false向右平移false个单位长度,可得false,所以不能得到false的图象,所以④错误.
综上可知,正确的为③.
故答案为: ③.
【点睛】
本题考查了三角函数解析式的求法,正弦函数的图像与性质的综合应用,属于中档题.
17.必要非充分条件
【分析】
利用等价命题的转化,再根据充分条件,必要条件的定义即可判断.
【详解】
当false时,有false,可知false;
当false时,一定有false,故false,
即“false”是“false”的必要条件.
又当false时,取false,可得false.所以false.
因此,“false”是“false”的必要非充分条件.
【点睛】
本题考查原命题与逆否命题为等价命题,考查充分、必要条件,属于基础题.
18.(1)false
(2)false.
【分析】
(1)直接代入数据化简得到答案.
(2)直接代入数据化简得到答案.
【详解】
(1)false
(2)false.
【点睛】
本题考查了求函数表达式,属于简单题.
19.(1)false; (2)当年3月1日动物种群数量约是750.
【分析】
(1)首先设种群数量false关于false的解析式为false,然后根据图象上最大值和最小值求false和false,根据周期求false,最后代入false ,false求false,得到函数的解析式;(2)3月1日是false ,根据(1)的解析式,求false时的函数值.
【详解】
(1)设种群数量false关于false的解析式为false,
则false,解得false.
又周期false,false,
false.
又当false时,false,
false,false,
false,false可取false,false.
(2)当false时,false,
即当年3月1日动物种群数量约是750.
【点睛】
本题考查根据函数的图象求三角函数的解析式,意在考查分析和整理数据,抽象和概括能力,属于中档题型.
20.(1)最小正周期是false,最小值为false.false的集合为false;
(2)false.
【分析】
(1)化简函数false,结合三角函数的图象与性质,即可求解;
(2)化简false,根据false,求得false的最大值为false,再根据题意,得到false,即可求解.
【详解】
(1)由题意,函数false,
可得其最小正周期是false,
当false,可得false,即false时,
函数false的最小值为false.
此时false的集合为false.
(2)由false
因为false,得false,则false,
所以false,
若false对于false恒成立,则false,
所以false,即求实数false的取值范围false.
【点睛】
本题主要考查了三角恒等变换,以及三角函数的图象与性质综合应用,其中解答中利用三角恒等变换的公式,求得函数的解析式,结合三角函数的图象与性质求解是解答的关键,着重考查了推理与运算能力,属于中档试题.
21.(1)1;(2)增函数,证明见解析;(3)false
【分析】
(1)根据函数奇函数的定义和条件false,求出k的值之后再验证是否满足函数的定义域关于原点对称即可;
(2)根据函数的单调性和对数函数的单调性即可证明;
(3)假设存在false,使得函数false在区间false上的值域为false,由false 在false上递增,程false在false上有两个不等实根,可得false的不等式组,解不等式即可得到实数false的取值范围,即可得到判断存在性.
【详解】
(1)因为函数false为奇函数,所以false,
即false对定义域内任意false恒成立,所以false,即false,
显然false,又当false时,false的定义域关于原点对称.
所以false为满足题意的值.
(2)结论:false在false,false上均为增函数.
证明:由(1)知false,其定义域为false,
任取false,不妨设false,则
false,
因为false,又false,
所以false,所以false,
即false,所以false在false上为增函数.
同理,false在false上为增函数.
(3)由(2)知false在false上为增函数,
又因为函数false在false上的值域为false,
所以false,且false,所以false,
即false是方程false的两实根,
问题等价于方程false在false上有两个不等实根,
令false,对称轴false
则false,
即false,解得false.
【点睛】
本题主要考查函数奇偶性和单调性的应用以及函数和方程的转化以及一元二次方程在给定区间上解的问题,根据函数奇偶性和单调性的定义函数性质是解决本题的关键,考查学生分析问题与解决问题的能力,是难题.
同课章节目录
