人教版数学八年级上册15.3分式方程第一课时课件(30张)
文档属性
| 名称 | 人教版数学八年级上册15.3分式方程第一课时课件(30张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 13:22:50 | ||
图片预览










文档简介
15.3分式方程
第一课时
目标
学习目标:
1.了解分式方程的概念.
2.会用去分母的方法解可化为一元一次方程的简单
的分式方程,体会化归思想和程序化思想.
3.了解解分式方程根需要进行检验的原因.
学习重点:
利用去分母的方法解分式方程.
关键词
1、 是什么方程?什么叫一元一次方程?
回顾
关键词
2、解一元一次方程的一般步骤是什么
去分母;
去括号;
移项;
合并同类项;
系数化为一。
回顾
关键词
探究
轮船在顺水中航行90千米所需的时间和逆水航行60千米所需的时间相同.已知水流的速度是30千米/时,求轮船在静水中的速度.
分析:设轮船在静水中的速度为x千米/时,根据题意,得
自主探究
关键词
上述方程和方程 有何不同?
小组讨论
关键词
总结:
分母里不含有未知数的方程叫整式方程.像这样,分母中含有未知数的方程叫做分式方程.
你还能举出一个分式方程的吗?
关键词
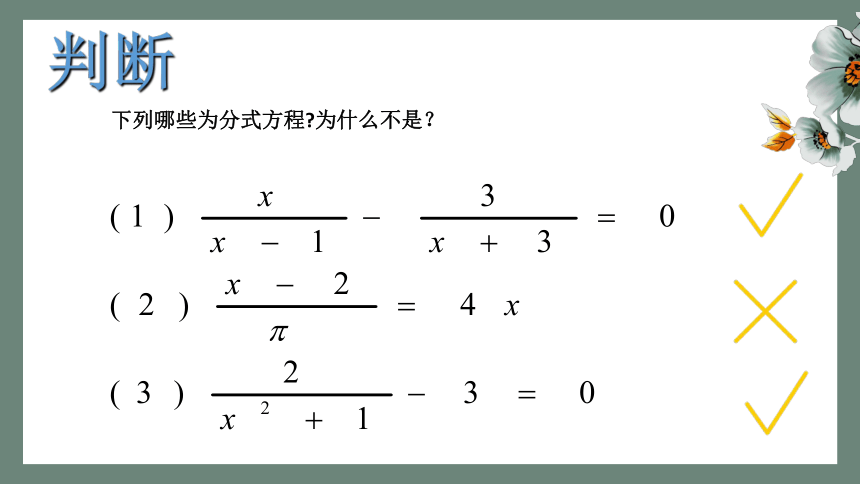
判断
下列哪些为分式方程?为什么不是?
关键词
判断
关键词
思考
分式方程有哪些特点?
特征:方程的两边的代数式是分式。或者说末知数在分母上的方程。
关键词
练习
下列式子中,属于分式方程的是 ,
属于整式方程的是 (填序号)说出各自的特点
关键词
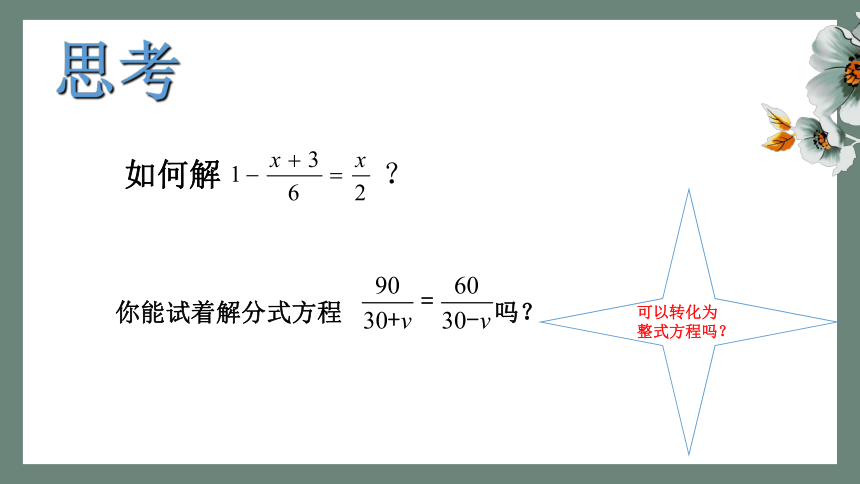
思考
如何解 ?
你能试着解分式方程 吗?
可以转化为整式方程吗?
关键词
思考
先去分母,将分式方程转化为整式方程,再解整式方程.
解分式方程
关键词
思考
(1)如何把分式方程转化为整式方程呢?
(2)怎样去分母?
(3)在方程两边乘以什么样的式子才能把每一个分母
都约去呢?
(4)这样做的依据是什么?
(1)分母中含有未知数的方程,通过去分母就化为整
式方程了.
(2)利用等式的性质2可以在方程两边都乘同一个式子
——各分母的最简公分母.
关键词
例如 解分式方程
解:方程两边同乘各分母的最简公分母
得
解得
关键词
你说我也说
解分式方程的过程,实质上是将分式方程两边乘以最简公分母,约去分母,把分式方程转化为整式方程。
解分式方程一般方法
关键词
练习
解:方程两边同乘各分母的最简公分母
得
解得
关键词
练习
关键词
练习
问题4 解分式方程:
追问1 你得到的解 是分式方程
的解吗?该如何验证呢?
是原分式方程变形后的整式方程的解,但不是
原分式方程的解.
追问2 上面两个分式方程的求解过程中,同样是
去分母将分式方程化为整式方程,为什么整式方程
的解 是分式方程
的解,而整式方程
的解 却不
却不是分式方程
的解?
原因:
在去分母的过程中,对原分式方程进行了变形,而
这种变形是否引起分式方程解的变化,主要取决于所乘
的最简公分母是否为0.
检验的方法主要有两种:
(1)将整式方程的解代入原分式方程,看左右两边是
否相等;
(2)将整式方程的解代入最简公分母,看是否为0.
显然,第2种方法比较简便!
问题5 回顾解分式方程 与方程
路和一般步骤吗?解分式方程应该注意什么?
的过程,你能概括出解分式方程的基本思
基本思路 将分式方程化为整式方程一般步骤:
(1)去分母;
(2)解整式方程;
(3)检验.
注意:
由于去分母后解得的整式方程的解不一定是原分式
方程的解,所以需要检验.
(2)解:方程两边同乘 ,得
=3.
化简,得 =3.
解得 =1.
检验:当 =1时, =0, =1不是原分式
方程的解,所以,原分式方程无解.
例 解下列方程:
解分式方程的步骤:
(1)去分母,将分式方程转化为整式方程;
(2)解这个整式方程;
(3)检验.
归纳解分式方程的步骤
练习 解下列方程:
关键词
整式方程
分式方程
类比
畅谈收获
1.教科书习题15.3第1(1)~(4)题.
2.同步118——119.
3.练习册134——136
布置小结
謝 謝
第一课时
目标
学习目标:
1.了解分式方程的概念.
2.会用去分母的方法解可化为一元一次方程的简单
的分式方程,体会化归思想和程序化思想.
3.了解解分式方程根需要进行检验的原因.
学习重点:
利用去分母的方法解分式方程.
关键词
1、 是什么方程?什么叫一元一次方程?
回顾
关键词
2、解一元一次方程的一般步骤是什么
去分母;
去括号;
移项;
合并同类项;
系数化为一。
回顾
关键词
探究
轮船在顺水中航行90千米所需的时间和逆水航行60千米所需的时间相同.已知水流的速度是30千米/时,求轮船在静水中的速度.
分析:设轮船在静水中的速度为x千米/时,根据题意,得
自主探究
关键词
上述方程和方程 有何不同?
小组讨论
关键词
总结:
分母里不含有未知数的方程叫整式方程.像这样,分母中含有未知数的方程叫做分式方程.
你还能举出一个分式方程的吗?
关键词
判断
下列哪些为分式方程?为什么不是?
关键词
判断
关键词
思考
分式方程有哪些特点?
特征:方程的两边的代数式是分式。或者说末知数在分母上的方程。
关键词
练习
下列式子中,属于分式方程的是 ,
属于整式方程的是 (填序号)说出各自的特点
关键词
思考
如何解 ?
你能试着解分式方程 吗?
可以转化为整式方程吗?
关键词
思考
先去分母,将分式方程转化为整式方程,再解整式方程.
解分式方程
关键词
思考
(1)如何把分式方程转化为整式方程呢?
(2)怎样去分母?
(3)在方程两边乘以什么样的式子才能把每一个分母
都约去呢?
(4)这样做的依据是什么?
(1)分母中含有未知数的方程,通过去分母就化为整
式方程了.
(2)利用等式的性质2可以在方程两边都乘同一个式子
——各分母的最简公分母.
关键词
例如 解分式方程
解:方程两边同乘各分母的最简公分母
得
解得
关键词
你说我也说
解分式方程的过程,实质上是将分式方程两边乘以最简公分母,约去分母,把分式方程转化为整式方程。
解分式方程一般方法
关键词
练习
解:方程两边同乘各分母的最简公分母
得
解得
关键词
练习
关键词
练习
问题4 解分式方程:
追问1 你得到的解 是分式方程
的解吗?该如何验证呢?
是原分式方程变形后的整式方程的解,但不是
原分式方程的解.
追问2 上面两个分式方程的求解过程中,同样是
去分母将分式方程化为整式方程,为什么整式方程
的解 是分式方程
的解,而整式方程
的解 却不
却不是分式方程
的解?
原因:
在去分母的过程中,对原分式方程进行了变形,而
这种变形是否引起分式方程解的变化,主要取决于所乘
的最简公分母是否为0.
检验的方法主要有两种:
(1)将整式方程的解代入原分式方程,看左右两边是
否相等;
(2)将整式方程的解代入最简公分母,看是否为0.
显然,第2种方法比较简便!
问题5 回顾解分式方程 与方程
路和一般步骤吗?解分式方程应该注意什么?
的过程,你能概括出解分式方程的基本思
基本思路 将分式方程化为整式方程一般步骤:
(1)去分母;
(2)解整式方程;
(3)检验.
注意:
由于去分母后解得的整式方程的解不一定是原分式
方程的解,所以需要检验.
(2)解:方程两边同乘 ,得
=3.
化简,得 =3.
解得 =1.
检验:当 =1时, =0, =1不是原分式
方程的解,所以,原分式方程无解.
例 解下列方程:
解分式方程的步骤:
(1)去分母,将分式方程转化为整式方程;
(2)解这个整式方程;
(3)检验.
归纳解分式方程的步骤
练习 解下列方程:
关键词
整式方程
分式方程
类比
畅谈收获
1.教科书习题15.3第1(1)~(4)题.
2.同步118——119.
3.练习册134——136
布置小结
謝 謝
