人教版八年级数学上册课件:12.2三角形全等的判定(共20张PPT)
文档属性
| 名称 | 人教版八年级数学上册课件:12.2三角形全等的判定(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 293.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 00:00:00 | ||
图片预览



文档简介
三角形全等的判定
第二课时
温故知新
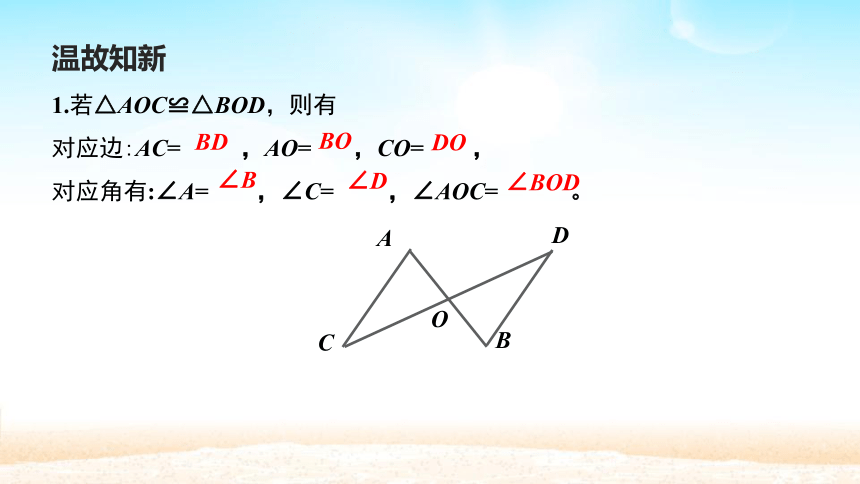
1.若△AOC≌△BOD,则有
对应边:AC= ,AO= ,CO= ,
对应角有:∠A= ,∠C= ,∠AOC= 。
A
B
O
C
D
BD
BO
DO
∠B
∠D
∠BOD
2.填空:
已知:AC=AD,BC=BD。求证:AB是∠DAC的平分线。
AC=AD( ),
BC=BD( ),
= ( ),
∴△ABC≌△ABD( )。
∴∠1=∠2( )。
∴AB是∠DAC的平分线(角平分线定义)。
A
B
C
D
1
2
已知
已知
SSS
证明:在△ABC和△ABD中,
AB AB 公共边
全等三角形的对应角相等
温故知新
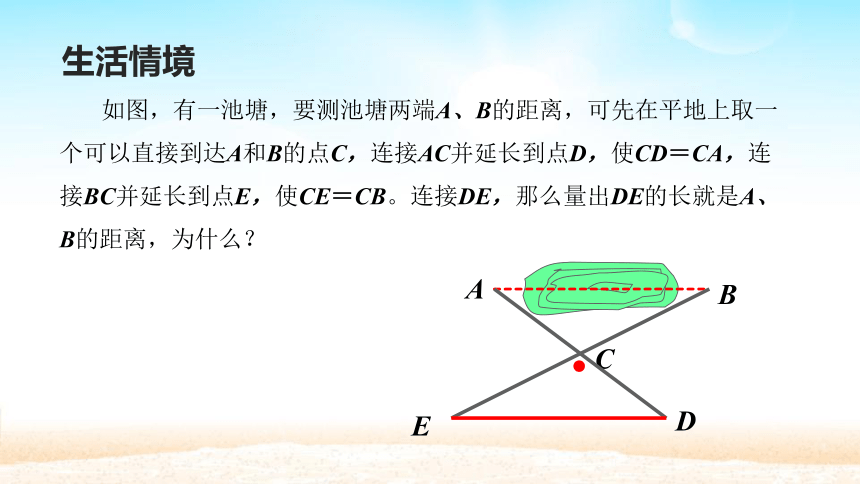
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB。连接DE,那么量出DE的长就是A、B的距离,为什么?
C
·
A
E
D
B
生活情境
作图探究
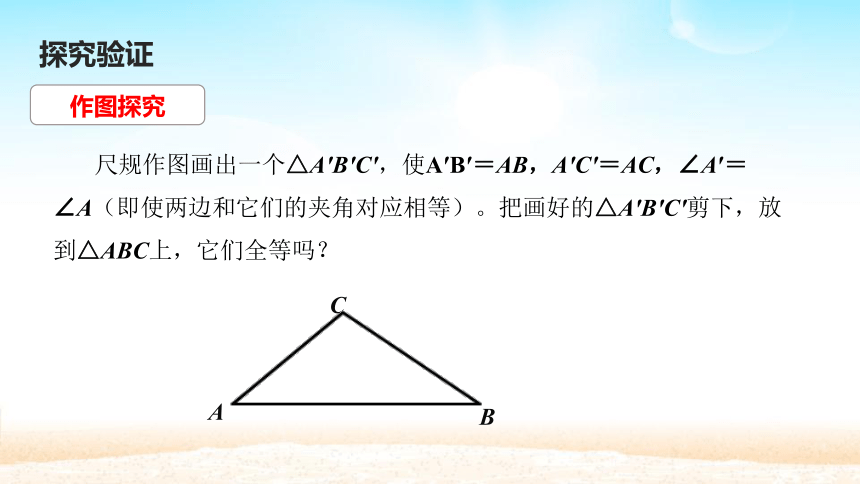
尺规作图画出一个△A′B′C′,使A′B′=AB,A′C′=AC,∠A′=∠A(即使两边和它们的夹角对应相等)。把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
A
B
C
探究验证
A
B
C
A′
D
E
B′
C′
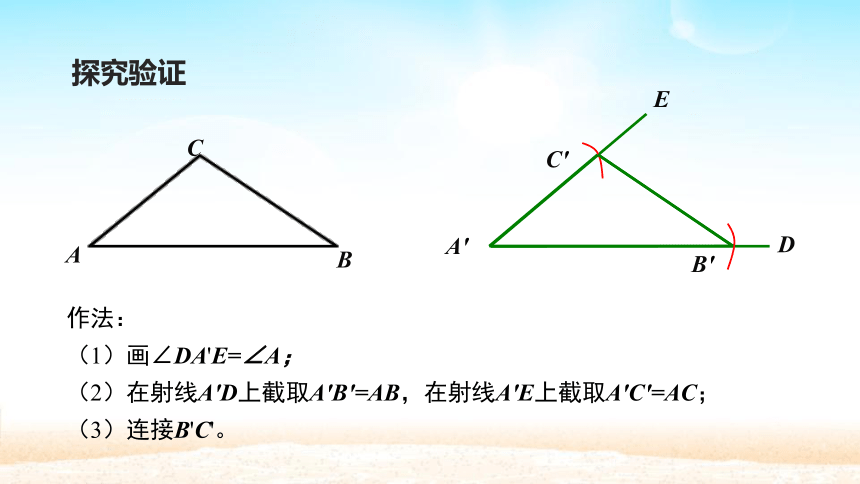
作法:
(1)画∠DA'E=∠A;
(2)在射线A'D上截取A'B'=AB,在射线A'E上截取A'C'=AC;
(3)连接B'C'。
探究验证
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(SAS)。
文字语言:两边和它们的夹角分别相等的两个三角形全等。
(简写成“边角边”或“SAS”)
几何语言:
AB=A′B′,
∠A=∠A′,
AC=A′C′,
A
B
C
A′
B′
C′
必须是两边“夹角”
“边角边”判定方法
探究验证
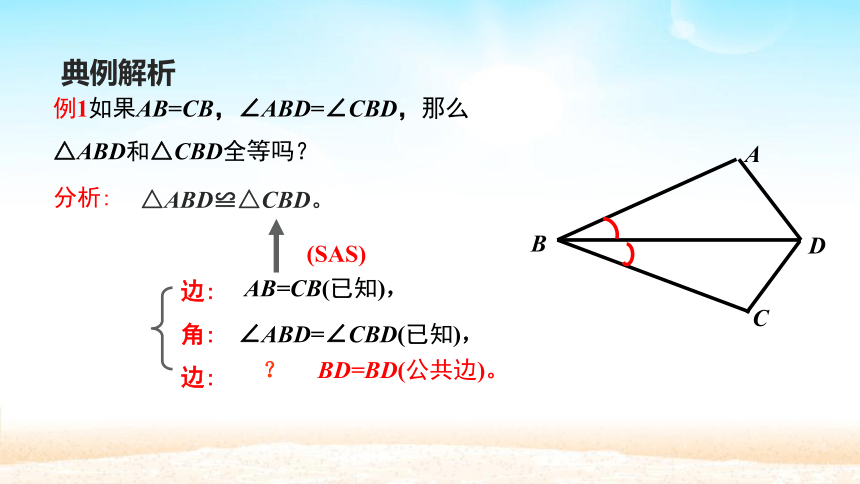
例1如果AB=CB,∠ABD=∠CBD,那么
△ABD和△CBD全等吗?
分析:
△ABD≌△CBD。
边:
角:
边:
AB=CB(已知),
∠ABD=∠CBD(已知),
?
A
B
C
D
(SAS)
BD=BD(公共边)。
典例解析
A
B
C
D
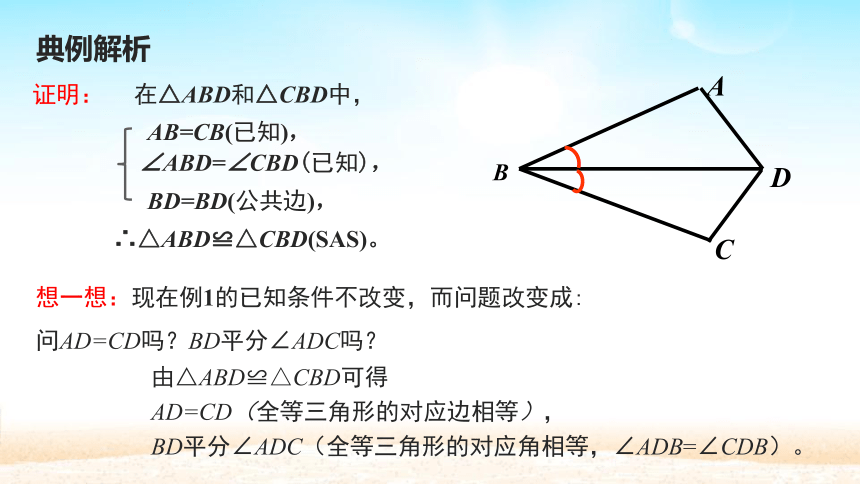
证明:
在△ABD和△CBD中,
AB=CB(已知),
∠ABD=∠CBD(已知),
BD=BD(公共边),
∴△ABD≌△CBD(SAS)。
想一想:现在例1的已知条件不改变,而问题改变成:
问AD=CD吗?BD平分∠ADC吗?
由△ABD≌△CBD可得
AD=CD(全等三角形的对应边相等),
BD平分∠ADC(全等三角形的对应角相等,∠ADB=∠CDB)。
典例解析
例2如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB。连接DE,那么量出DE的长就是A、B的距离,为什么?
C
·
A
E
D
B
分析:
如果能证明△ABC≌△DEC,就可以得出AB=DE。
由题意知,△ABC和△DEC具备“边角边”的条件。
典例解析
证明:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS)。
∴AB=DE
(全等三角形的对应边相等)。
AC=DC(已知),
∠1=∠2(对顶角相等),
CB=EC(已知),
C
·
A
E
D
B
1
2
证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决。
归纳
典例解析
1.下列图形中有没有全等三角形,并说明全等的理由。
甲
8cm
9cm
丙
8cm
9cm
8cm
9cm
乙
30°
30°
30°
甲与丙全等,SAS。
练一练
当堂练习
2.在下列推理中填写需要补充的条件,使结论成立。
(已知),
=
∠A=∠A(公共角),
=
A
D
C
B
E
∴△AEC≌△ADB()。
在△AEC和△ADB中,
AB
AC
AD
AE
SAS
注意:“SAS”中的角必须是两边的夹角,“A”必须在中间。
。
当堂练习
3.已知:如图,AB=DB,CB=EB,∠1=∠2,求证:∠A=∠D。
证明:∵∠1=∠2(已知)
∴∠1+∠DBC=∠2+∠DBC(等式的性质),
即∠ABC=∠DBE。
在△ABC和△DBE中,
AB=DB(已知),
∠ABC=∠DBE(已证),
CB=EB(已知),
∴△ABC≌△DBE(SAS)。
∴∠A=∠D(全等三角形的对应角相等)。
1
A
2
C
B
D
E
当堂练习
4.如图,点E、F在AC上,AD//BC,AD=CB,AE=CF。
求证:△AFD≌△CEB。
F
A
B
D
C
E
证明:
∵AD//BC,
∴∠A=∠C,
∵AE=CF,
在△AFD和△CEB中,
AD=CB
∠A=∠C
AF=CE
∴△AFD≌△CEB(SAS)。
∴AE+EF=CF+EF,
即AF=CE。
(已知),
(已证),
(已证),
当堂练习
两个大小不同的等腰直角三角板如图①放置,图②是由它抽象出的几何图形,点B,C,E在同一条直线上,连接CD。求证:CD⊥BE。
证△ABE≌△ACD(SAS),得∠ACD=∠ABE=45°,
∴∠BCD=∠ACB+∠ACD=45°+45°=90°,
即CD⊥BE。
探索拓展
B
A
C
D
想一想:如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC。固定住长木棍,转动短木棍,得到△ABD。这个实验说明了什么?
这说明,有两边和其中一边的对角分别相等的两个三角形不一定全等。
归纳
△ABC和△ABD满足AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等。
“SSA”不能作为三角形全等的判定定理
我来做
数学活动
今天我们学了什么?
今天我们悟到什么?
今天的质疑和发现?
梳理反思
今天我们学了什么?
今天我们悟到什么?
三角形全等的判定(SAS)
边角边
内容
有两边及夹角对应相等的两个三角形全等
(简写成“SAS”)
应用
为证明线段和角相等提供了新的证法
注意
1。已知两边,必须找“夹角”
2。已知一角和这角的一夹边,必须找这角的另一夹边
梳理反思
谢 谢
第二课时
温故知新
1.若△AOC≌△BOD,则有
对应边:AC= ,AO= ,CO= ,
对应角有:∠A= ,∠C= ,∠AOC= 。
A
B
O
C
D
BD
BO
DO
∠B
∠D
∠BOD
2.填空:
已知:AC=AD,BC=BD。求证:AB是∠DAC的平分线。
AC=AD( ),
BC=BD( ),
= ( ),
∴△ABC≌△ABD( )。
∴∠1=∠2( )。
∴AB是∠DAC的平分线(角平分线定义)。
A
B
C
D
1
2
已知
已知
SSS
证明:在△ABC和△ABD中,
AB AB 公共边
全等三角形的对应角相等
温故知新
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB。连接DE,那么量出DE的长就是A、B的距离,为什么?
C
·
A
E
D
B
生活情境
作图探究
尺规作图画出一个△A′B′C′,使A′B′=AB,A′C′=AC,∠A′=∠A(即使两边和它们的夹角对应相等)。把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
A
B
C
探究验证
A
B
C
A′
D
E
B′
C′
作法:
(1)画∠DA'E=∠A;
(2)在射线A'D上截取A'B'=AB,在射线A'E上截取A'C'=AC;
(3)连接B'C'。
探究验证
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(SAS)。
文字语言:两边和它们的夹角分别相等的两个三角形全等。
(简写成“边角边”或“SAS”)
几何语言:
AB=A′B′,
∠A=∠A′,
AC=A′C′,
A
B
C
A′
B′
C′
必须是两边“夹角”
“边角边”判定方法
探究验证
例1如果AB=CB,∠ABD=∠CBD,那么
△ABD和△CBD全等吗?
分析:
△ABD≌△CBD。
边:
角:
边:
AB=CB(已知),
∠ABD=∠CBD(已知),
?
A
B
C
D
(SAS)
BD=BD(公共边)。
典例解析
A
B
C
D
证明:
在△ABD和△CBD中,
AB=CB(已知),
∠ABD=∠CBD(已知),
BD=BD(公共边),
∴△ABD≌△CBD(SAS)。
想一想:现在例1的已知条件不改变,而问题改变成:
问AD=CD吗?BD平分∠ADC吗?
由△ABD≌△CBD可得
AD=CD(全等三角形的对应边相等),
BD平分∠ADC(全等三角形的对应角相等,∠ADB=∠CDB)。
典例解析
例2如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB。连接DE,那么量出DE的长就是A、B的距离,为什么?
C
·
A
E
D
B
分析:
如果能证明△ABC≌△DEC,就可以得出AB=DE。
由题意知,△ABC和△DEC具备“边角边”的条件。
典例解析
证明:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS)。
∴AB=DE
(全等三角形的对应边相等)。
AC=DC(已知),
∠1=∠2(对顶角相等),
CB=EC(已知),
C
·
A
E
D
B
1
2
证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决。
归纳
典例解析
1.下列图形中有没有全等三角形,并说明全等的理由。
甲
8cm
9cm
丙
8cm
9cm
8cm
9cm
乙
30°
30°
30°
甲与丙全等,SAS。
练一练
当堂练习
2.在下列推理中填写需要补充的条件,使结论成立。
(已知),
=
∠A=∠A(公共角),
=
A
D
C
B
E
∴△AEC≌△ADB()。
在△AEC和△ADB中,
AB
AC
AD
AE
SAS
注意:“SAS”中的角必须是两边的夹角,“A”必须在中间。
。
当堂练习
3.已知:如图,AB=DB,CB=EB,∠1=∠2,求证:∠A=∠D。
证明:∵∠1=∠2(已知)
∴∠1+∠DBC=∠2+∠DBC(等式的性质),
即∠ABC=∠DBE。
在△ABC和△DBE中,
AB=DB(已知),
∠ABC=∠DBE(已证),
CB=EB(已知),
∴△ABC≌△DBE(SAS)。
∴∠A=∠D(全等三角形的对应角相等)。
1
A
2
C
B
D
E
当堂练习
4.如图,点E、F在AC上,AD//BC,AD=CB,AE=CF。
求证:△AFD≌△CEB。
F
A
B
D
C
E
证明:
∵AD//BC,
∴∠A=∠C,
∵AE=CF,
在△AFD和△CEB中,
AD=CB
∠A=∠C
AF=CE
∴△AFD≌△CEB(SAS)。
∴AE+EF=CF+EF,
即AF=CE。
(已知),
(已证),
(已证),
当堂练习
两个大小不同的等腰直角三角板如图①放置,图②是由它抽象出的几何图形,点B,C,E在同一条直线上,连接CD。求证:CD⊥BE。
证△ABE≌△ACD(SAS),得∠ACD=∠ABE=45°,
∴∠BCD=∠ACB+∠ACD=45°+45°=90°,
即CD⊥BE。
探索拓展
B
A
C
D
想一想:如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC。固定住长木棍,转动短木棍,得到△ABD。这个实验说明了什么?
这说明,有两边和其中一边的对角分别相等的两个三角形不一定全等。
归纳
△ABC和△ABD满足AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等。
“SSA”不能作为三角形全等的判定定理
我来做
数学活动
今天我们学了什么?
今天我们悟到什么?
今天的质疑和发现?
梳理反思
今天我们学了什么?
今天我们悟到什么?
三角形全等的判定(SAS)
边角边
内容
有两边及夹角对应相等的两个三角形全等
(简写成“SAS”)
应用
为证明线段和角相等提供了新的证法
注意
1。已知两边,必须找“夹角”
2。已知一角和这角的一夹边,必须找这角的另一夹边
梳理反思
谢 谢
