1.1生活中的立体图形第2课时-北师大版七年级数学上册课件(25张)
文档属性
| 名称 | 1.1生活中的立体图形第2课时-北师大版七年级数学上册课件(25张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 00:00:00 | ||
图片预览


文档简介
1 生活中的立体图形(第2课时)
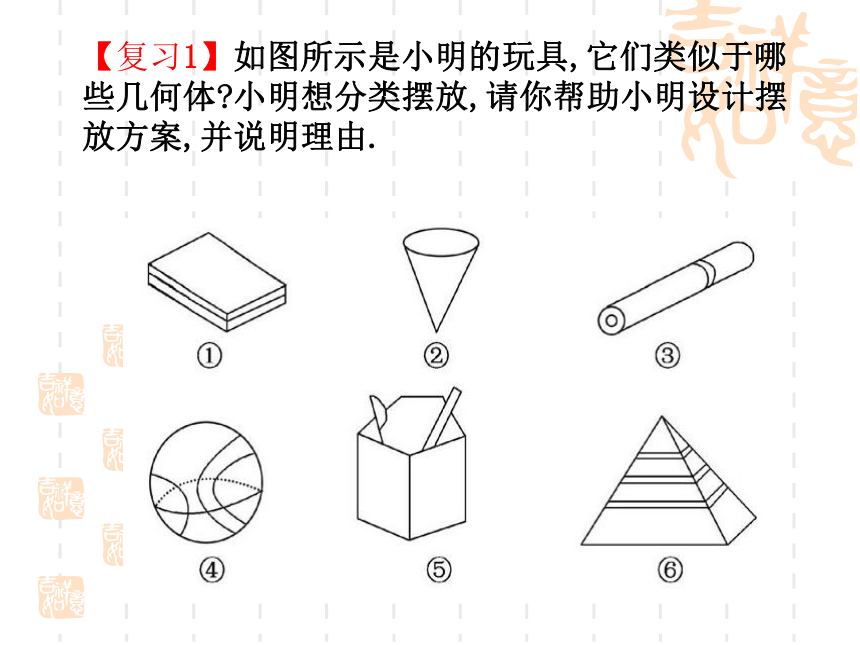
【复习1】如图所示是小明的玩具,它们类似于哪些几何体?小明想分类摆放,请你帮助小明设计摆放方案,并说明理由.
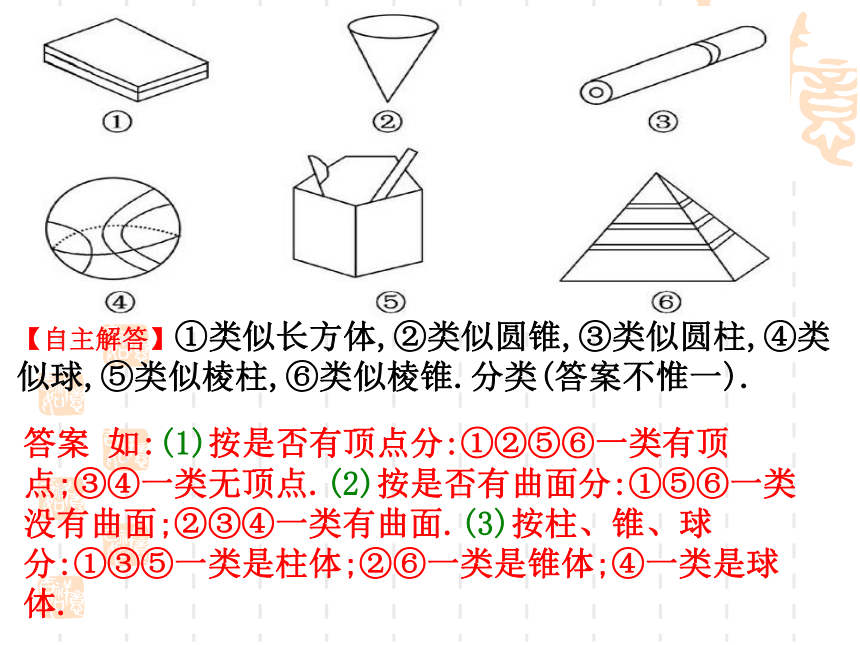
【自主解答】①类似长方体,②类似圆锥,③类似圆柱,④类似球,⑤类似棱柱,⑥类似棱锥.分类(答案不惟一).
答案 如:(1)按是否有顶点分:①②⑤⑥一类有顶点;③④一类无顶点.(2)按是否有曲面分:①⑤⑥一类没有曲面;②③④一类有曲面.(3)按柱、锥、球分:①③⑤一类是柱体;②⑥一类是锥体;④一类是球体.
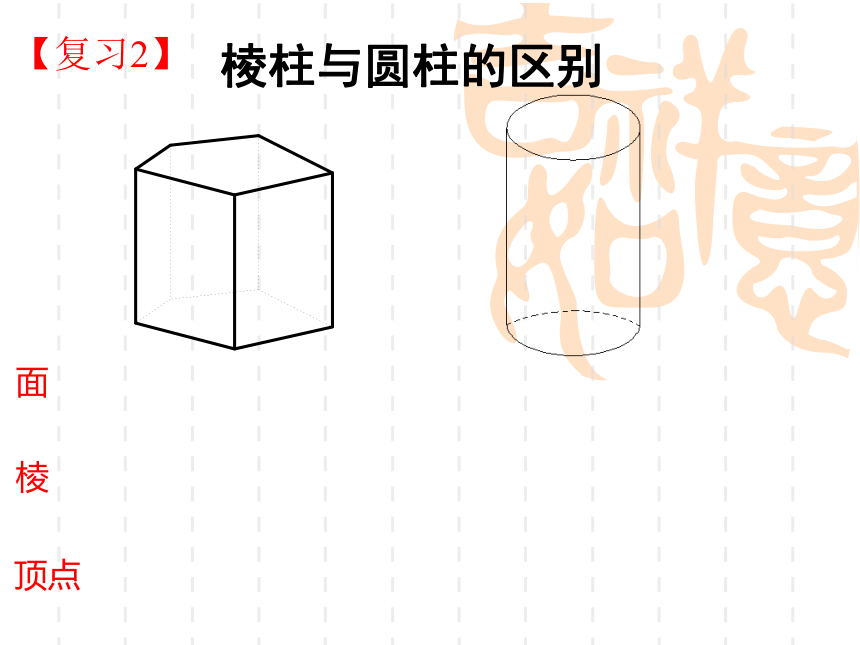
棱柱与圆柱的区别
面
棱
顶点
【复习2】
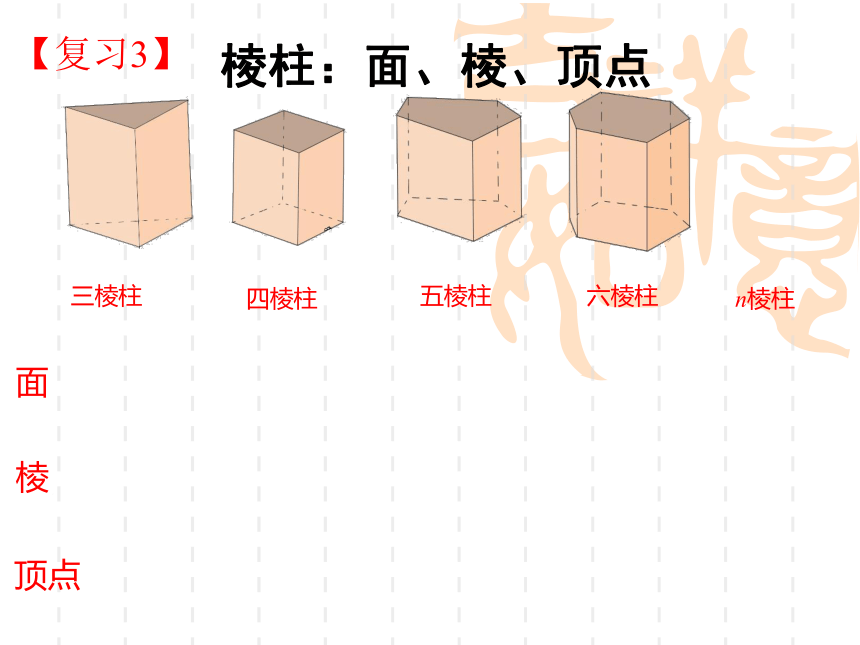
三棱柱
四棱柱
五棱柱
六棱柱
n棱柱
棱柱:面、棱、顶点
面
棱
顶点
【复习3】
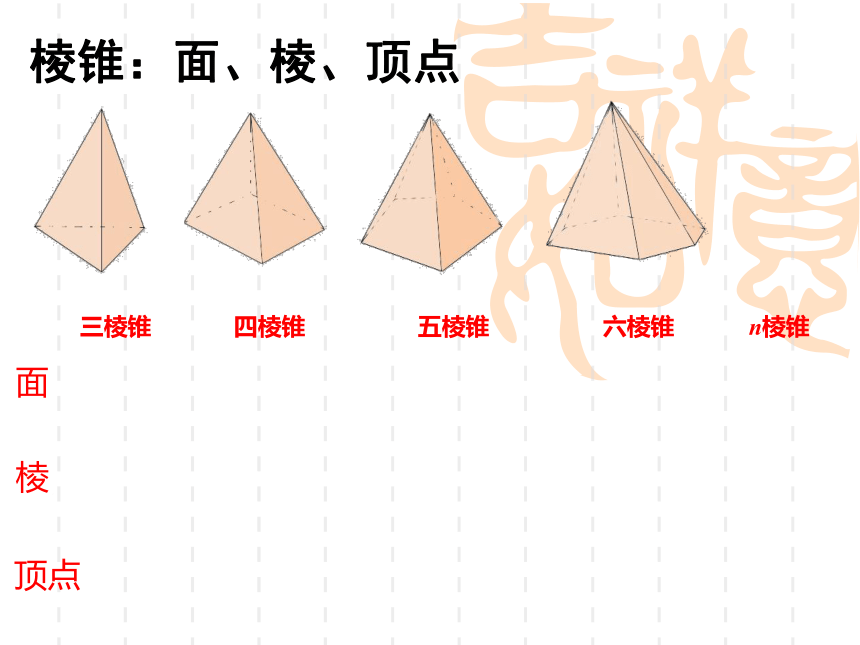
三棱锥
四棱锥
五棱锥
六棱锥
n棱锥
面
棱
顶点
棱锥:面、棱、顶点
世间万物都是由一些基本元素构成的,那么构成这些图形的基本元素是什么呢?
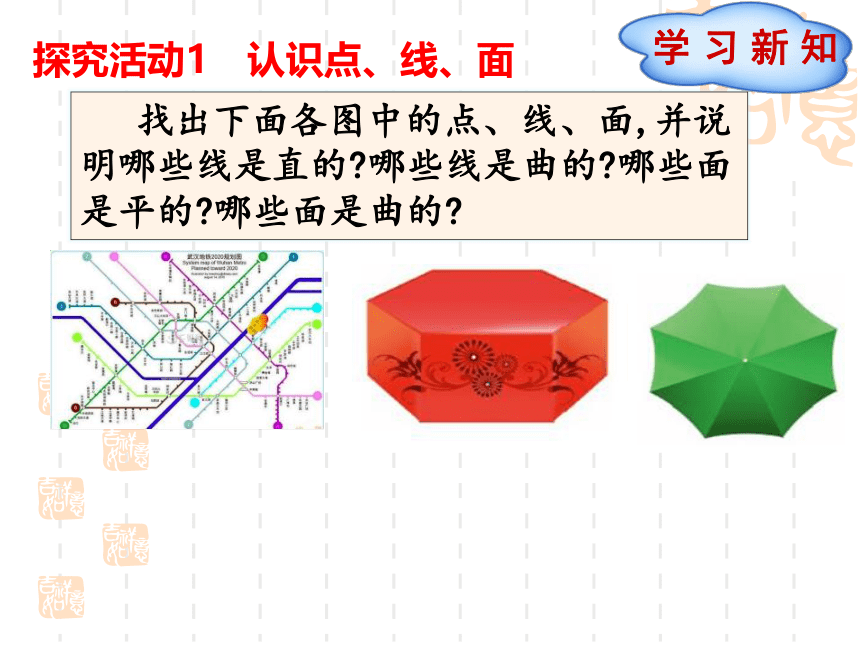
探究活动1 认识点、线、面
找出下面各图中的点、线、面,并说明哪些线是直的?哪些线是曲的?哪些面是平的?哪些面是曲的?
学 习 新 知
结合下图所示的几何体完成以下内容,小组内交流.
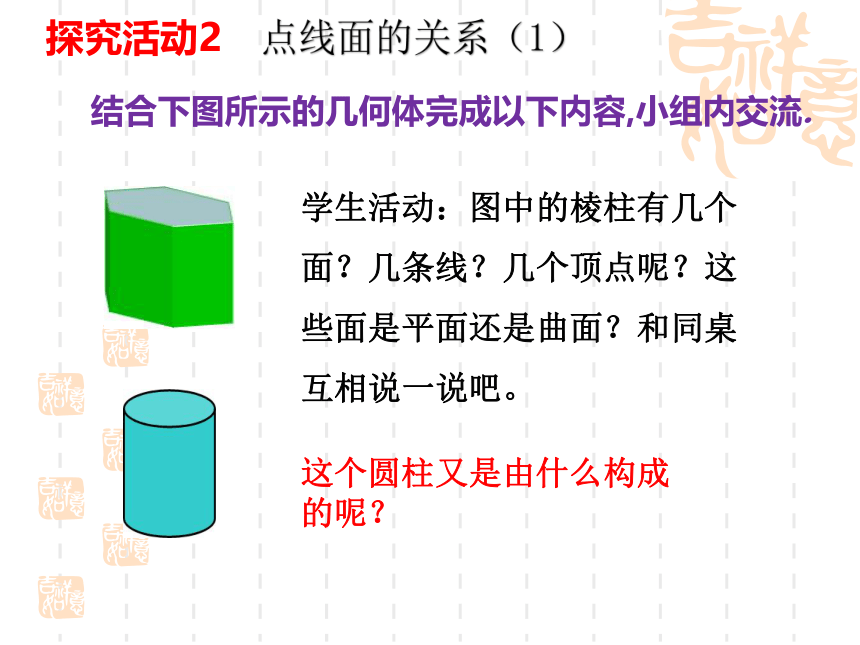
探究活动2 点线面的关系(1)
学生活动:图中的棱柱有几个面?几条线?几个顶点呢?这些面是平面还是曲面?和同桌互相说一说吧。
这个圆柱又是由什么构成的呢?
几何体
名称
几何体的组成
圆柱
长方体
正方体
圆锥
球
由大小相同且互相平行的两个底面(圆)和一个侧面(曲面)围成
由大小相同且互相平行的两个底面(长方形)和四个侧面(长方形)围成
由大小相同且互相平行的两个底面(正方形)和四个侧面(正方形)围成,或者说由六个完全相同的正方形围成
由一个底面(圆)和一个侧面(曲面)围成,有一个“尖尖的角”(顶点)
由一个曲面围成,没有底面,没有侧面,没有顶点
……
静态
面面相交得到线
线线相交得到点
面与面相交的地方得到一条线。
线与线相交的地方就是它们的公共点,也就是交点。
乒乓球(点)运动的轨迹是 ______。
乒乓球发球机
转笔刀削笔
旋转门旋转
门叶( )转动形成圆柱( )的门。
刀锋( )转动把铅笔削乘木屑片( )。
观察下图,你发现了什么?
线
线
面
面
体
探究活动2 点线面的关系(2)
点动成线
线动成面
面动成体
点线面在运动过程中与几何体的关系:
探究活动2 点线面的关系(2)
点,线,面,体关系
你能举出生活中类似以上三幅图的例子吗?
点线面关系图
探究活动3 常见几何体的形成
(1)如图所示的各个花瓶的表面可以看做由哪个平面图形绕虚线旋转一周而得到的?用线连一连.
(2)你能想象出圆柱、圆锥、球是由什么平面图形旋转而成的吗?
18
练习:把下面第一行的平面图形绕线旋转一周,便能形成第二行的某个几何体,请用虚线连一连:
1 2 3 4 5
A B C D E
(1)两平面相交,交线是 ,
一平面与一个曲面相交,交线是 ;?
(2)中国武术中有“枪扎一条线,棍扫一大片”这样的说法,这句话说明 ;?
(3)如右图所示,以BC所在直线为轴,旋转一周,求所得的立体图形的体积.
例题
直线
曲线
点动成线,线动成面
解:(3)旋转而成的立体图形是圆锥,其底面半径为4 cm,高为3 cm,所以体积为
20
1.多姿多彩的图形是由点、线、面、体组成。点是构成图形的基本元素。
2.点无大小,线有直线和曲线,面有平的面和曲的面。
3.点动成线,线动成面,面动成体。
4.体由面围成,面与面相交成线,线与线相交成点。
● 你学到了什么?
拓展提高
练习一:
(1)线与线相交,形成的是( )。
A.点 B.线 C.面 D.体
(2)一只蚂蚁行走的路线可以解释为( )。
A.点动成线 B.线动成面
C.面动成体 D.以上答案都不对
(3)将半圆绕它的直径旋转一周形成的几何是( )。
A.圆柱 B.圆锥 C.球 D.正方体
A
A
C
拓展提高
(4)下面属于现象属于线动成面的实际应用的
是_____。(多选)
① 笔尖在纸上快速滑动写出一个又一个字,
②自行车的辐条运动形成的几何图形,
③汽车雨刷在挡风玻璃上刷出的痕迹,
④旋转一扇门,门在空中运动的痕迹。
②③
(5)如图所示,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,请你把有对应关系的平面图形与立体图形用线连接起来.
(6)已知长方形的长3厘米,宽1厘米,将这个长方形绕一边所在直线旋转一周形成圆柱求所形成的圆柱体积及表面积;
几何体
柱体
锥体
球体
圆柱
棱柱
圆锥
棱锥
所有侧棱长都相等
上下底面的形状相同
侧面都是长方形
n棱柱有(n+2)个面,2n个顶点,3n条棱
课堂小结
【复习1】如图所示是小明的玩具,它们类似于哪些几何体?小明想分类摆放,请你帮助小明设计摆放方案,并说明理由.
【自主解答】①类似长方体,②类似圆锥,③类似圆柱,④类似球,⑤类似棱柱,⑥类似棱锥.分类(答案不惟一).
答案 如:(1)按是否有顶点分:①②⑤⑥一类有顶点;③④一类无顶点.(2)按是否有曲面分:①⑤⑥一类没有曲面;②③④一类有曲面.(3)按柱、锥、球分:①③⑤一类是柱体;②⑥一类是锥体;④一类是球体.
棱柱与圆柱的区别
面
棱
顶点
【复习2】
三棱柱
四棱柱
五棱柱
六棱柱
n棱柱
棱柱:面、棱、顶点
面
棱
顶点
【复习3】
三棱锥
四棱锥
五棱锥
六棱锥
n棱锥
面
棱
顶点
棱锥:面、棱、顶点
世间万物都是由一些基本元素构成的,那么构成这些图形的基本元素是什么呢?
探究活动1 认识点、线、面
找出下面各图中的点、线、面,并说明哪些线是直的?哪些线是曲的?哪些面是平的?哪些面是曲的?
学 习 新 知
结合下图所示的几何体完成以下内容,小组内交流.
探究活动2 点线面的关系(1)
学生活动:图中的棱柱有几个面?几条线?几个顶点呢?这些面是平面还是曲面?和同桌互相说一说吧。
这个圆柱又是由什么构成的呢?
几何体
名称
几何体的组成
圆柱
长方体
正方体
圆锥
球
由大小相同且互相平行的两个底面(圆)和一个侧面(曲面)围成
由大小相同且互相平行的两个底面(长方形)和四个侧面(长方形)围成
由大小相同且互相平行的两个底面(正方形)和四个侧面(正方形)围成,或者说由六个完全相同的正方形围成
由一个底面(圆)和一个侧面(曲面)围成,有一个“尖尖的角”(顶点)
由一个曲面围成,没有底面,没有侧面,没有顶点
……
静态
面面相交得到线
线线相交得到点
面与面相交的地方得到一条线。
线与线相交的地方就是它们的公共点,也就是交点。
乒乓球(点)运动的轨迹是 ______。
乒乓球发球机
转笔刀削笔
旋转门旋转
门叶( )转动形成圆柱( )的门。
刀锋( )转动把铅笔削乘木屑片( )。
观察下图,你发现了什么?
线
线
面
面
体
探究活动2 点线面的关系(2)
点动成线
线动成面
面动成体
点线面在运动过程中与几何体的关系:
探究活动2 点线面的关系(2)
点,线,面,体关系
你能举出生活中类似以上三幅图的例子吗?
点线面关系图
探究活动3 常见几何体的形成
(1)如图所示的各个花瓶的表面可以看做由哪个平面图形绕虚线旋转一周而得到的?用线连一连.
(2)你能想象出圆柱、圆锥、球是由什么平面图形旋转而成的吗?
18
练习:把下面第一行的平面图形绕线旋转一周,便能形成第二行的某个几何体,请用虚线连一连:
1 2 3 4 5
A B C D E
(1)两平面相交,交线是 ,
一平面与一个曲面相交,交线是 ;?
(2)中国武术中有“枪扎一条线,棍扫一大片”这样的说法,这句话说明 ;?
(3)如右图所示,以BC所在直线为轴,旋转一周,求所得的立体图形的体积.
例题
直线
曲线
点动成线,线动成面
解:(3)旋转而成的立体图形是圆锥,其底面半径为4 cm,高为3 cm,所以体积为
20
1.多姿多彩的图形是由点、线、面、体组成。点是构成图形的基本元素。
2.点无大小,线有直线和曲线,面有平的面和曲的面。
3.点动成线,线动成面,面动成体。
4.体由面围成,面与面相交成线,线与线相交成点。
● 你学到了什么?
拓展提高
练习一:
(1)线与线相交,形成的是( )。
A.点 B.线 C.面 D.体
(2)一只蚂蚁行走的路线可以解释为( )。
A.点动成线 B.线动成面
C.面动成体 D.以上答案都不对
(3)将半圆绕它的直径旋转一周形成的几何是( )。
A.圆柱 B.圆锥 C.球 D.正方体
A
A
C
拓展提高
(4)下面属于现象属于线动成面的实际应用的
是_____。(多选)
① 笔尖在纸上快速滑动写出一个又一个字,
②自行车的辐条运动形成的几何图形,
③汽车雨刷在挡风玻璃上刷出的痕迹,
④旋转一扇门,门在空中运动的痕迹。
②③
(5)如图所示,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,请你把有对应关系的平面图形与立体图形用线连接起来.
(6)已知长方形的长3厘米,宽1厘米,将这个长方形绕一边所在直线旋转一周形成圆柱求所形成的圆柱体积及表面积;
几何体
柱体
锥体
球体
圆柱
棱柱
圆锥
棱锥
所有侧棱长都相等
上下底面的形状相同
侧面都是长方形
n棱柱有(n+2)个面,2n个顶点,3n条棱
课堂小结
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
