2.4.1有理数的加法-北师大版七年级数学上册课件(26张)
文档属性
| 名称 | 2.4.1有理数的加法-北师大版七年级数学上册课件(26张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 00:00:00 | ||
图片预览





文档简介
有理数的加法
课前复习
1、一个不等于0的有理数可看作由哪两个部分组成?
(符号、数值)
2、比较下列各组数绝对值哪个大?
(1)-22与15; (2)- 与
(3)2.7与- 3 .5
1
2
1
3
+7 +3.2 -4 -2
学习目标:
1、能概述有理数的加法法则,并熟记
2、能够运用有理数的加法法则进行简单计算。
问题情境
某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不回答得0分。
我们可以把答对一题记为“+1”,答错一题记为“-1”,此时的分数为(+1)+(-1)=0
+
+
+
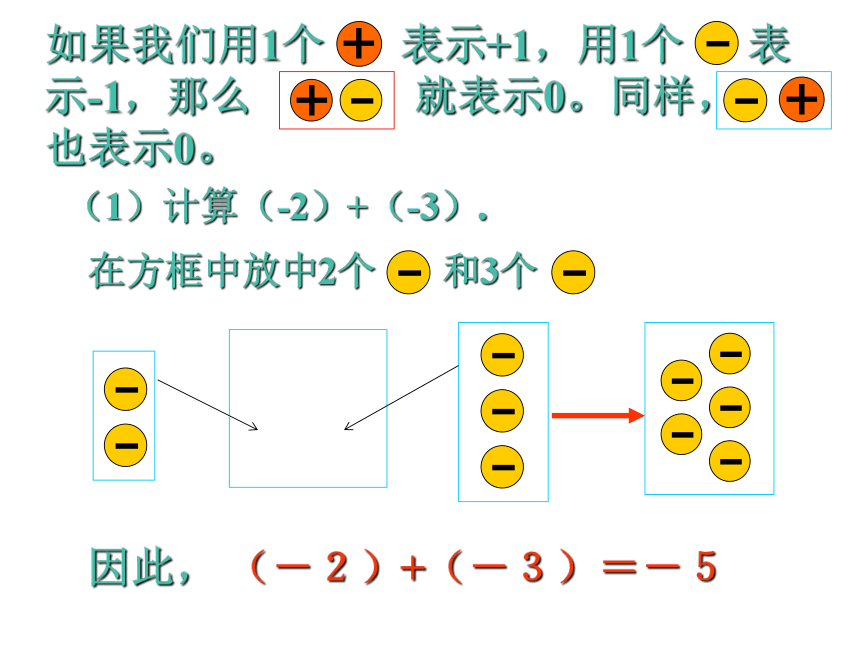
如果我们用1个 表示+1,用1个 表示-1,那么 就表示0。同样, 也表示0。
(1)计算(-2)+(-3).
在方框中放中2个 和3个
因此, (-2)+(-3)=-5
0
1
2
3
4
5
-1
-2
-3
-4
-5
(-2)
(-3)
+
=
-5
(-2)
(-3)
思考:能不能借助数轴计算(-2)+(-3)= ?
+
+
+
+
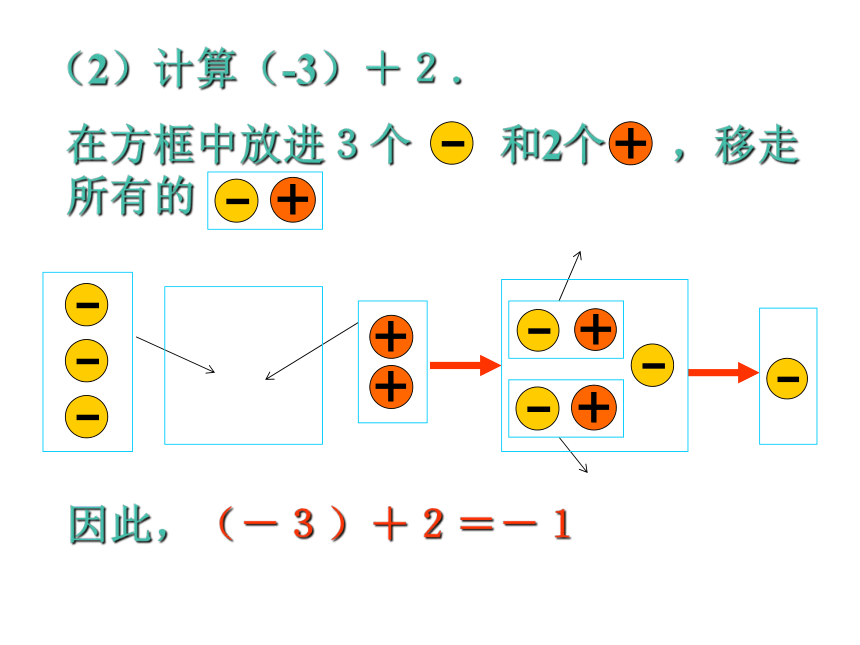
(2)计算(-3)+2.
+
在方框中放进3个 和2个 ,移走所有的
+
因此,(-3)+2=-1
0
1
2
3
4
5
-1
-2
-3
-4
-5
2
-3
(-3)
2
+
=
-1
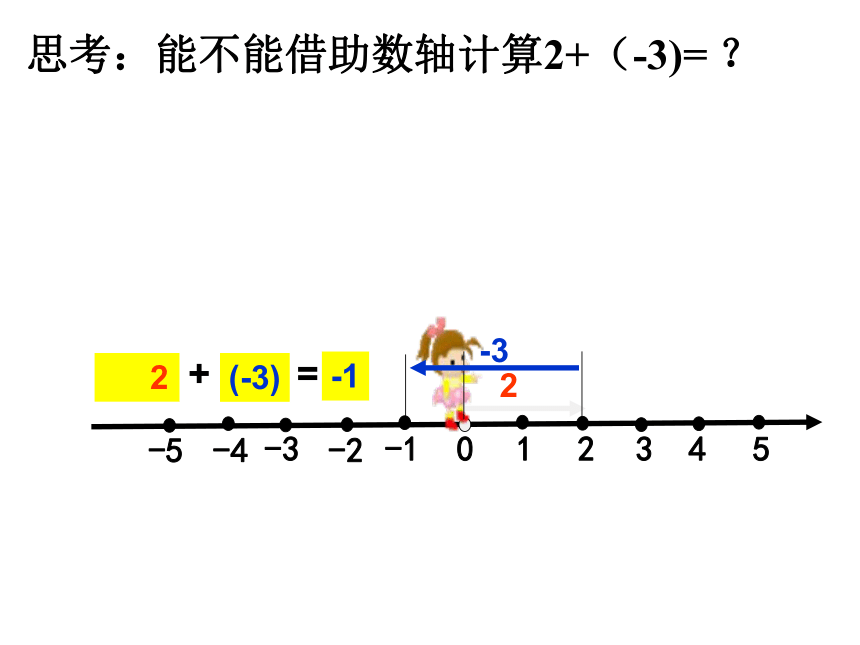
思考:能不能借助数轴计算2+(-3)= ?
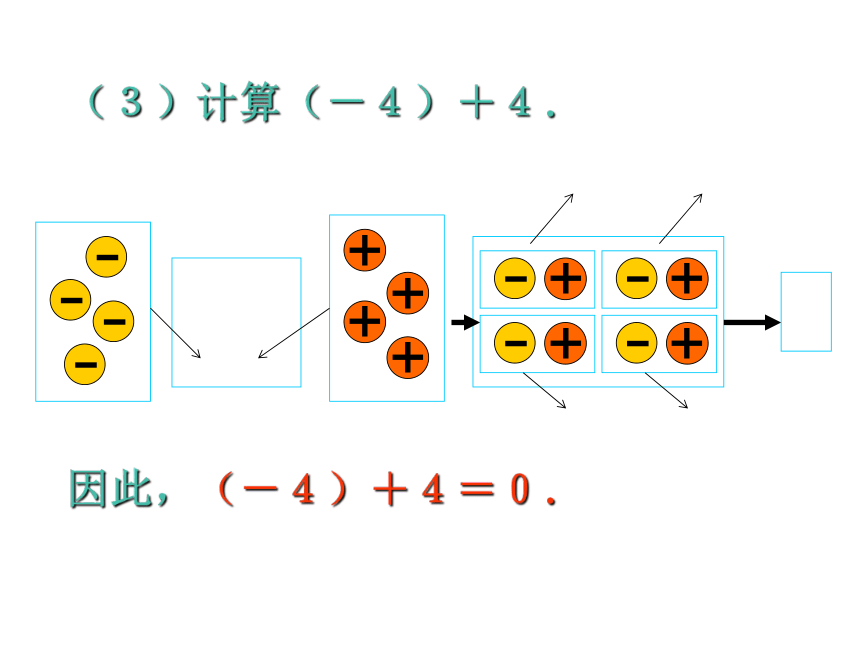
(3)计算(-4)+4.
因此,(-4)+4=0.
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
计算(-2)+ 3
+
+
在方框中放进3个 和2个 ,移走所有的 .
因此,3+(-2)=1
0
1
2
3
4
5
-1
-2
-3
-4
-5
-2
3
3
(-2)
+
=
1
思考:能不能借助数轴计算(-2)+3= ?
( - 4 ) + ( - 8 ) = - ( 4 + 8 )= - 12
↓ ↓ ↓
( - 9 ) + (+ 2) = - ( 9 - 2) = -7
↓ ↓ ↓
两个有理数相加,和的符号怎样确定?和的绝对值如何确定?
议一议
两个加数的绝对 值相加
较大的绝对值减去较小的绝对值
同号两数相加
取相同符号
异号两数相加
取绝对值较大的数的符号
有理数加法法则
(1)同号两数相加,取相同符号,并把绝对值相加.
(2)异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并将较大的绝对值减较小的绝对值.
(3)一个数同0相加,仍得这个数.
总结归纳
归纳有理数的加法法则为一句话
同加 异减 符号大
例1.计算下列各题:
(1)180+(-10) (2)(-10)+(-1)
(3)5+(-5) (4)0+(-2)
解:(1)180+(-10)
=+(180-10)
=170
(2)(-10)+(-1)
= -(10+1)
= -11
(异号两数相加)
(取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值)
(同号两数相加)
(取相同的符号,并把绝对值相加)
(3)5+(-5)
=0
(互为相反数的两数相加)
(4)0+(-2)
=-2
(一个数和0相加)
先确定和的符号;
再进行绝对值的加减运算
判断类型(同号、异号等);
我会算
2.请同学们完成书上P36的随堂练习.
( 1 ) (-25)+(-7);??? ( 2 ) (-13)+5;? ?
( 3 ) (-23)+0; (4 ) 45+(-45)
(1)原式= -(25+7) (2)原式= -(13-5)
= -32 = -8
3. 请同学们完成书上P36习题2.4的第一题
(3)、(4)、(5)、(6)、(7)
(1)(-0.6)+(-2.7); ? (2)3.7+(-8.4);?
(3)(-0.6)+3; (4)3.22+1.78;
(5)7+(-3.3);?? (6)(-1.9)+(-0.11).
当堂练习
1.计算:
答案:(1)-3.3 (2)-4.7 (3)2.4 (4)5
(5)3.7 (6)-2.01
练习一 (口答思考过程和结果)
1、 (-7)+1
2、 (-8)+(-3)
3、(-9)+(+5)
4、 (-6)+(+6)
5、 (-7)+0
6、 8+(-1)
7、 3+8
1. 每袋大米的标准质量为50千克,超过标准质量的数记为正数,不足标准质量的数记为负数,10袋大米称重记录如下(单位:千克): +1.2,-0.4, +1, 0, -1.1, -0.5, +0.3, +0.5,-0.6, -0.9,问这10袋大米总计超过多少千克或不足多少千克? 10袋大米的总质量是多少千克?
有理数加法的应用
二
红队
黄队
蓝队
净胜球
红队
4:1
0:1
2
黄队
1:4
1:0
-2
蓝队
1:0
0:1
0
例2 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
有理数加法的应用
二
解:每个队的进球总数记为正数,失球总数记为负数,这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2
蓝队共进( )球,失( )球,净胜球数为( ).
1
1
(+1)+(-1)=0
2.股民默克上星期五以收盘价67元买进某公司股票1000股,下表为本周内每日该股票的涨跌情况:
星 期
一
二
三
四
五
每股涨跌/元
4
4.5
-1
-2.5
-6
(1)星期三收盘时,每股多少元?
(2)本周内每股最高价为多少元?最低价为多少元?
解:(1)67+(+4)+(+4.5)+(-1)=74.5(元),故星期三收盘时,每股74.5元;
星 期
一
二
三
四
五
每股涨跌/元
4
4.5
-1
-2.5
-6
(2)本周内每股最高价为多少元?最低价为多少元?
解:(2)周一:67+4=71元,
周二:71+4.5=75.5元,
周三:75.5+(-1)=74.5元,
周四:74.5+(-2.5)=72元,
周五:72+(-6)=66元,
∴本周内每股最高价为75.5元,最低价为66元.
思考题:用“>”或“<”号填空:
(1)如果a>0,b>0,那么a+b 0;
(2)如果a<0,b<0,那么a+b 0;
(3)如果a>0,b<0,|a|>|b|,那么a+b 0;
(4)如果a<0,b>0,|a|>|b|,那么a+b 0.
思 维 拓 展
>
<
>
<
2.计算,(分数小数可以互相转化)
1.两个有理数相加,”一观察,二确定,三求和”首先观察判断加法类型,再确定和的符号,最后求和的绝对值
2. 有理数加法法则及其应用。
3. 注意异号的情况。
归纳小结
课前复习
1、一个不等于0的有理数可看作由哪两个部分组成?
(符号、数值)
2、比较下列各组数绝对值哪个大?
(1)-22与15; (2)- 与
(3)2.7与- 3 .5
1
2
1
3
+7 +3.2 -4 -2
学习目标:
1、能概述有理数的加法法则,并熟记
2、能够运用有理数的加法法则进行简单计算。
问题情境
某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不回答得0分。
我们可以把答对一题记为“+1”,答错一题记为“-1”,此时的分数为(+1)+(-1)=0
+
+
+
如果我们用1个 表示+1,用1个 表示-1,那么 就表示0。同样, 也表示0。
(1)计算(-2)+(-3).
在方框中放中2个 和3个
因此, (-2)+(-3)=-5
0
1
2
3
4
5
-1
-2
-3
-4
-5
(-2)
(-3)
+
=
-5
(-2)
(-3)
思考:能不能借助数轴计算(-2)+(-3)= ?
+
+
+
+
(2)计算(-3)+2.
+
在方框中放进3个 和2个 ,移走所有的
+
因此,(-3)+2=-1
0
1
2
3
4
5
-1
-2
-3
-4
-5
2
-3
(-3)
2
+
=
-1
思考:能不能借助数轴计算2+(-3)= ?
(3)计算(-4)+4.
因此,(-4)+4=0.
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
计算(-2)+ 3
+
+
在方框中放进3个 和2个 ,移走所有的 .
因此,3+(-2)=1
0
1
2
3
4
5
-1
-2
-3
-4
-5
-2
3
3
(-2)
+
=
1
思考:能不能借助数轴计算(-2)+3= ?
( - 4 ) + ( - 8 ) = - ( 4 + 8 )= - 12
↓ ↓ ↓
( - 9 ) + (+ 2) = - ( 9 - 2) = -7
↓ ↓ ↓
两个有理数相加,和的符号怎样确定?和的绝对值如何确定?
议一议
两个加数的绝对 值相加
较大的绝对值减去较小的绝对值
同号两数相加
取相同符号
异号两数相加
取绝对值较大的数的符号
有理数加法法则
(1)同号两数相加,取相同符号,并把绝对值相加.
(2)异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并将较大的绝对值减较小的绝对值.
(3)一个数同0相加,仍得这个数.
总结归纳
归纳有理数的加法法则为一句话
同加 异减 符号大
例1.计算下列各题:
(1)180+(-10) (2)(-10)+(-1)
(3)5+(-5) (4)0+(-2)
解:(1)180+(-10)
=+(180-10)
=170
(2)(-10)+(-1)
= -(10+1)
= -11
(异号两数相加)
(取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值)
(同号两数相加)
(取相同的符号,并把绝对值相加)
(3)5+(-5)
=0
(互为相反数的两数相加)
(4)0+(-2)
=-2
(一个数和0相加)
先确定和的符号;
再进行绝对值的加减运算
判断类型(同号、异号等);
我会算
2.请同学们完成书上P36的随堂练习.
( 1 ) (-25)+(-7);??? ( 2 ) (-13)+5;? ?
( 3 ) (-23)+0; (4 ) 45+(-45)
(1)原式= -(25+7) (2)原式= -(13-5)
= -32 = -8
3. 请同学们完成书上P36习题2.4的第一题
(3)、(4)、(5)、(6)、(7)
(1)(-0.6)+(-2.7); ? (2)3.7+(-8.4);?
(3)(-0.6)+3; (4)3.22+1.78;
(5)7+(-3.3);?? (6)(-1.9)+(-0.11).
当堂练习
1.计算:
答案:(1)-3.3 (2)-4.7 (3)2.4 (4)5
(5)3.7 (6)-2.01
练习一 (口答思考过程和结果)
1、 (-7)+1
2、 (-8)+(-3)
3、(-9)+(+5)
4、 (-6)+(+6)
5、 (-7)+0
6、 8+(-1)
7、 3+8
1. 每袋大米的标准质量为50千克,超过标准质量的数记为正数,不足标准质量的数记为负数,10袋大米称重记录如下(单位:千克): +1.2,-0.4, +1, 0, -1.1, -0.5, +0.3, +0.5,-0.6, -0.9,问这10袋大米总计超过多少千克或不足多少千克? 10袋大米的总质量是多少千克?
有理数加法的应用
二
红队
黄队
蓝队
净胜球
红队
4:1
0:1
2
黄队
1:4
1:0
-2
蓝队
1:0
0:1
0
例2 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
有理数加法的应用
二
解:每个队的进球总数记为正数,失球总数记为负数,这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2
蓝队共进( )球,失( )球,净胜球数为( ).
1
1
(+1)+(-1)=0
2.股民默克上星期五以收盘价67元买进某公司股票1000股,下表为本周内每日该股票的涨跌情况:
星 期
一
二
三
四
五
每股涨跌/元
4
4.5
-1
-2.5
-6
(1)星期三收盘时,每股多少元?
(2)本周内每股最高价为多少元?最低价为多少元?
解:(1)67+(+4)+(+4.5)+(-1)=74.5(元),故星期三收盘时,每股74.5元;
星 期
一
二
三
四
五
每股涨跌/元
4
4.5
-1
-2.5
-6
(2)本周内每股最高价为多少元?最低价为多少元?
解:(2)周一:67+4=71元,
周二:71+4.5=75.5元,
周三:75.5+(-1)=74.5元,
周四:74.5+(-2.5)=72元,
周五:72+(-6)=66元,
∴本周内每股最高价为75.5元,最低价为66元.
思考题:用“>”或“<”号填空:
(1)如果a>0,b>0,那么a+b 0;
(2)如果a<0,b<0,那么a+b 0;
(3)如果a>0,b<0,|a|>|b|,那么a+b 0;
(4)如果a<0,b>0,|a|>|b|,那么a+b 0.
思 维 拓 展
>
<
>
<
2.计算,(分数小数可以互相转化)
1.两个有理数相加,”一观察,二确定,三求和”首先观察判断加法类型,再确定和的符号,最后求和的绝对值
2. 有理数加法法则及其应用。
3. 注意异号的情况。
归纳小结
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
