4.4.2一次函数的应用(1)-北师大版八年级数学上册课件(17张)
文档属性
| 名称 | 4.4.2一次函数的应用(1)-北师大版八年级数学上册课件(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 263.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 00:00:00 | ||
图片预览



文档简介
4.4.2 一次函数的应用
第四章 一次函数
1、求一次函数关系式关键是要确定关系式中的
待定系数_ _、___的值,所以需要___个条
件.求正比例函数关系式只需要___个条件。
2、用待定系数法求一次函数关系式的步骤?
① 设-根据已知关系设____ ___;
② 代-把已知条件代入___ __;
③ 求-求出____值,____值;
④ 写-把___和____的值代回所设的关系式。
复习回顾(1分钟)
k
b
2
1
函数关系式
函数关系式
k
b
k
b
学习目标:(1分钟)
1.会利用一次函数的图象和关系式解决简
单实际问题;
2.了解一元一次方程与一次函数之间的联系.
自学指导1(1分钟)
学生自学,教师巡视(4分钟)
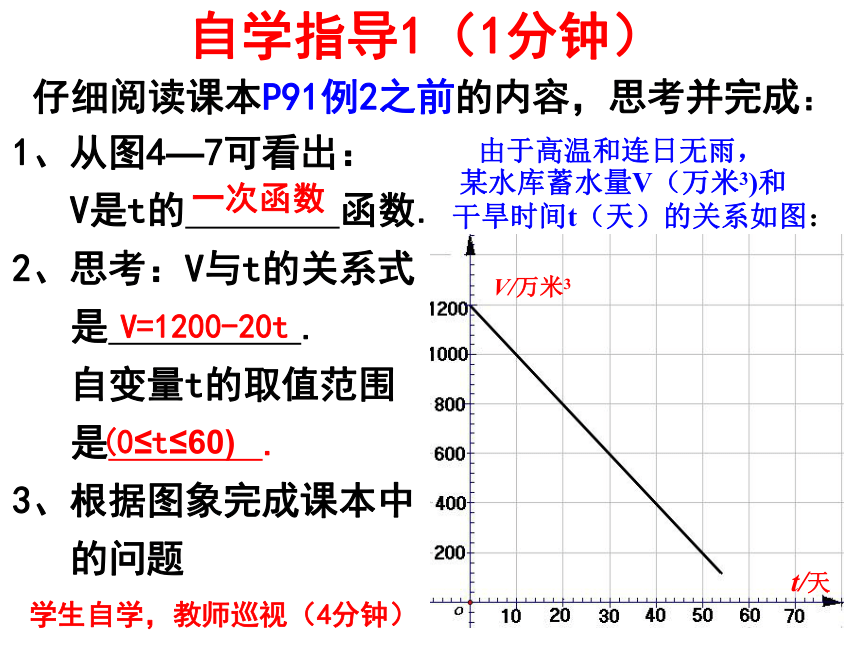
仔细阅读课本P91例2之前的内容,思考并完成:
1、从图4—7可看出:
V是t的 函数.
2、思考:V与t的关系式
是 .
自变量t的取值范围
是 .
3、根据图象完成课本中
的问题
由于高温和连日无雨,
某水库蓄水量V(万米3)和
干旱时间t(天)的关系如图:
V/万米3
t/天
(0≤t≤60)
一次函数
V=1200-20t
自学检测1:(6分钟)
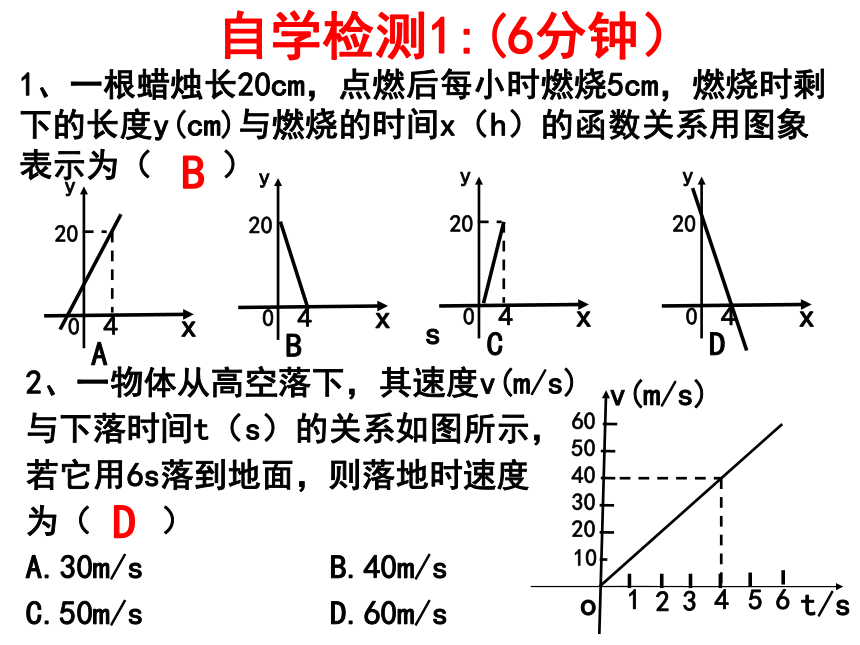
1、一根蜡烛长20cm,点燃后每小时燃烧5cm,燃烧时剩下的长度y(cm)与燃烧的时间x(h)的函数关系用图象表示为( )
x
0
y
4
20
A
B
y
x
0
4
20
B
y
x
0
4
20
C
y
x
0
4
20
D
2、一物体从高空落下,其速度v(m/s)
与下落时间t(s)的关系如图所示,
若它用6s落到地面,则落地时速度
为( )
A.30m/s B.40m/s
C.50m/s D.60m/s
s
t/s
o
3
10
2
v(m/s)
1
4
5
6
20
30
40
50
60
D
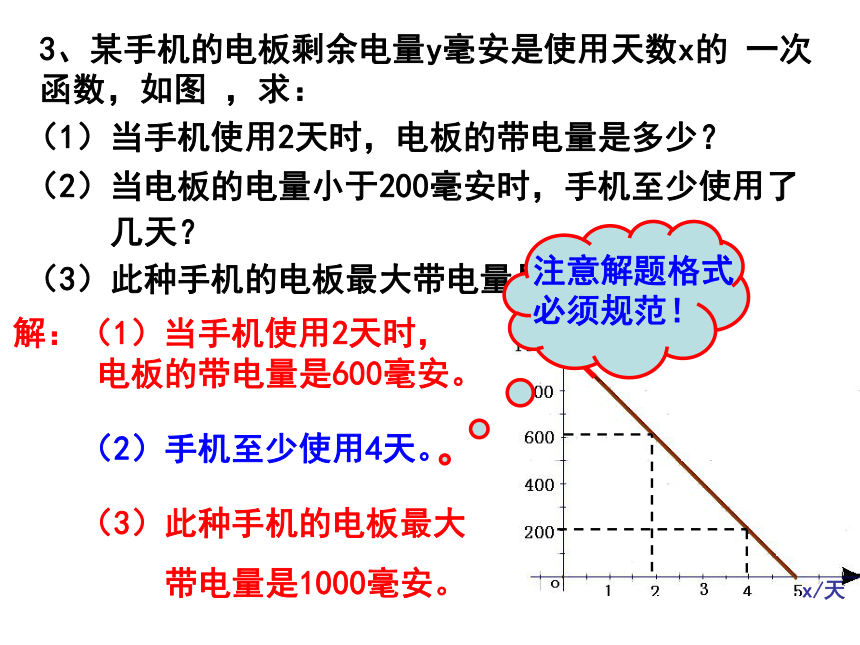
3、某手机的电板剩余电量y毫安是使用天数x的 一次函数,如图 ,求:
y/毫安
x/天
(3)此种手机的电板最大带电量是多少?
(1)当手机使用2天时,电板的带电量是多少?
(2)当电板的电量小于200毫安时,手机至少使用了
几天?
解:(1)当手机使用2天时,
电板的带电量是600毫安。
(2)手机至少使用4天。
(3)此种手机的电板最大
带电量是1000毫安。
注意解题格式
必须规范!
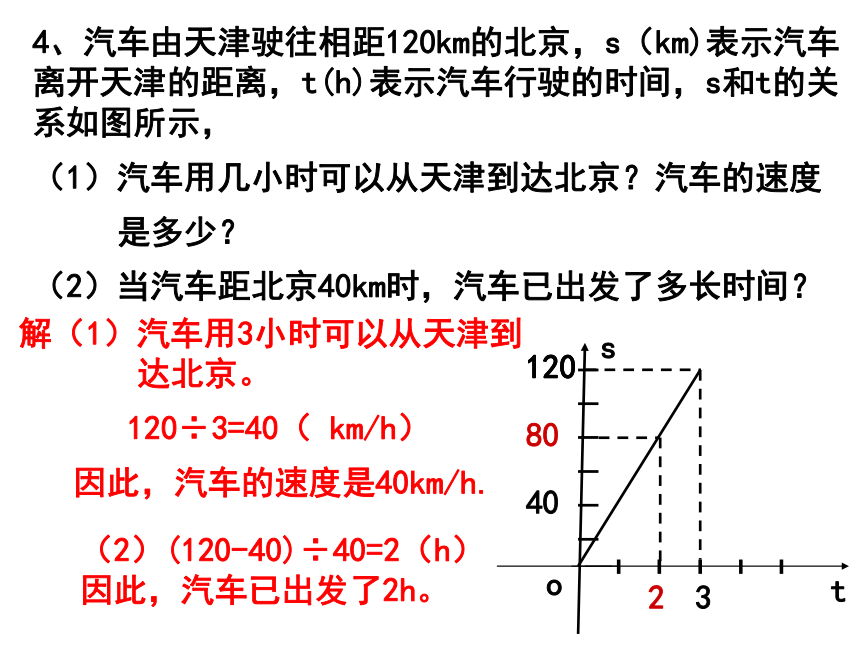
4、汽车由天津驶往相距120km的北京,s(km)表示汽车离开天津的距离,t(h)表示汽车行驶的时间,s和t的关系如图所示,
(1)汽车用几小时可以从天津到达北京?汽车的速度
是多少?
(2)当汽车距北京40km时,汽车已出发了多长时间?
t
s
o
3
120
80
40
2
(2)(120-40)÷40=2(h)
因此,汽车已出发了2h。
120
解(1)汽车用3小时可以从天津到
达北京。
120÷3=40( km/h)
因此,汽车的速度是40km/h.
自学指导2(1分钟)
学生自学,教师巡视(3分钟)
1、认真自学例2;
2、完成P92做一做;
3、思考:一次函数y=kx+b与方程kx+b=0有什
么联系?
仔细阅读课本P91例2—P92的内容,思考并完成:
2、一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系?
从“形”的方面看,函数y=0.5x+1与x轴交点的横坐标,即为方程0.5x+1=0的解。
2
0
1
3
1
2
3
-1
-2
-3
-1
-2
-3
x
y
1.看图填空:(1)当y=0时,x=__;
(2)直线的函数关系式是________
2.一元一次方程0.5x+1=0的解是x= .
直线y=0.5x+1与x轴的交点坐标是 .
-2
y=0.5x+1
1、讨论课本P92“做一做”和“议一议”,解答下列问题:
(-2,0)
-2
更正、点拨(3分钟)
从“数”的方面看,当一次函数y=0.5x+1的函数值为0时,相应的自变量的值即为方程0.5x+1=0的解。
(1)排水前,蓄水池共有水______m3,
最多用_____小时排完;
(3)排水6小时后,蓄水池的剩余
水量是______,当蓄水池中只剩50m3的水
时,排水时间是____小时。
1、如图,是蓄水池的剩余水量V(m3)与排水时间t(h)之间的关系图形,请根据图象解答下列问题:
(2)每小时排水____m3 ,剩余
水量V与排水时间t的函数关
系式是___________,自变量
的取值范围是________.
400
8
50
V=-50t+400
0≤t≤8
100
t(h)
0
4
8
200
400
V(m3)
7
自学检测2:(8分钟)
4、如图,直线y=kx+b与x轴交于
点A(-4,0),则关于x的一
元一次方程kx+b=0的解
是___ .
2、方程2x-5=0的解是____ ,直线y=2x-5
与x轴的交点坐标是____ .
3、已知函数y=kx+b的图象如图所示,则方程
kx+b=0的解是( )
A.x=1 B.x=2
C.x=0 D.不能确定
x=-4
x=2.5
(2.5,0)
X
y
O
A
-4
y=kx+b
2
0
1
1
2
-1
-1
x
y
A
小结(1分钟)
注意:(1)明确坐标轴代表的实际意义。
(2)自变量的取值范围。
3、理解一元一次方程与一次函数的联系。
1、会从图象的形状、图象上点的坐标、某一量
的取值范围获取准确的信息。
2、理解图象与两坐标轴的交点坐标的实际意义。
1、某植物t天后的高度为ycm,
l反映了y与t之间的关系,
根据图象回答下列问题:
(课本P93 T2)
(1)3天后该植物高度为多少?
(2)预测植物12天后的高度;
(3)几天后该植物高度为10cm?
(4)图象对应的一次函数y=kt+b中,k和t的实际意义分
别是什么?
当堂训练(15分钟)
2
1
3
4
5
6
7
y/cm
l
1
2
3
4
5
6
7
t/天
8
9
10
0
8
9
10
解:3天后该植物高度5cm.
12天后的高度11.4cm.
10天高度为10cm
k表示增长的速度,b表示开始时的高度。
2、直线y=ax+b与x轴的交点坐标为(3,0)则方程ax+b=0的解是______;已知3x+m=0的解是x=-5,则直线y=3x+m与x轴的交点坐标是_______。
x=3
(-5,0)
3、某市自来水公司采取分段收费标准,右图反映的是每月收取水费y (元)与用水量x(吨)之间的函数关系。
(1)小明家五月份用水8吨,应交费______元;
(2)按上述收费标准,小明家三、四月份分别交水费26元和18元,四月份比三月份节约用水______吨。
X/吨
y/元
0
20
20
10
50
16
3
4、某汽车离开某城市的距离y(km)与行驶时间t(h)之间的关系式为y=kt+30,其图象如图所示:
(1)在1h至3h之间,汽车行驶的路程是多少?
(2)你能确定k的值吗?这里k的具体含义是什么?
解:(1)当t=1时,y=90;当t=3时,y=_____;
210-90=120
所以,在1时至3时之间,汽车行驶的路程是______千米
210
120
(2)把t=1,y=90代人
得K=60,K表示汽车行驶的速度。
课本P93“数学理解” T3
x/kg
o
y
/cm
20
20
10
解:(1)弹簧未挂物体时的长度
是10cm;
(2)弹簧所挂物体的最大质量是
20kg,此时弹簧的长度是20cm
选做题:5、弹簧的长度与所挂物体的质量的关系如图
所示,观察图象回答:
(1)弹簧未挂物体时的长度是多少?
(2)弹簧所挂物体的最大质量是多少?这时弹簧的长
度是多少?
(3)在弹性限度内,求出y(cm)与x(kg)的函数关系式。
(3)
6、如图4,点A的坐标为(4,0),点P在第一象限且在
直线y=-x+6上.
(1)设点P坐标为(x,y),写出△OPA的面积S与x之
间的关系式(其中P点横坐标在O与A点之间变化;
(2)当S=10时,求点P坐标;
(3)若△OPA是以OA为底边的等腰三角形,你能求出P
的坐标吗?若能,请求出坐标;若不能,请说明
理由.
(2)P点坐标为(1,5).
(3)P点坐标为(2,4).
解:(1)
(0<x≤4)
第四章 一次函数
1、求一次函数关系式关键是要确定关系式中的
待定系数_ _、___的值,所以需要___个条
件.求正比例函数关系式只需要___个条件。
2、用待定系数法求一次函数关系式的步骤?
① 设-根据已知关系设____ ___;
② 代-把已知条件代入___ __;
③ 求-求出____值,____值;
④ 写-把___和____的值代回所设的关系式。
复习回顾(1分钟)
k
b
2
1
函数关系式
函数关系式
k
b
k
b
学习目标:(1分钟)
1.会利用一次函数的图象和关系式解决简
单实际问题;
2.了解一元一次方程与一次函数之间的联系.
自学指导1(1分钟)
学生自学,教师巡视(4分钟)
仔细阅读课本P91例2之前的内容,思考并完成:
1、从图4—7可看出:
V是t的 函数.
2、思考:V与t的关系式
是 .
自变量t的取值范围
是 .
3、根据图象完成课本中
的问题
由于高温和连日无雨,
某水库蓄水量V(万米3)和
干旱时间t(天)的关系如图:
V/万米3
t/天
(0≤t≤60)
一次函数
V=1200-20t
自学检测1:(6分钟)
1、一根蜡烛长20cm,点燃后每小时燃烧5cm,燃烧时剩下的长度y(cm)与燃烧的时间x(h)的函数关系用图象表示为( )
x
0
y
4
20
A
B
y
x
0
4
20
B
y
x
0
4
20
C
y
x
0
4
20
D
2、一物体从高空落下,其速度v(m/s)
与下落时间t(s)的关系如图所示,
若它用6s落到地面,则落地时速度
为( )
A.30m/s B.40m/s
C.50m/s D.60m/s
s
t/s
o
3
10
2
v(m/s)
1
4
5
6
20
30
40
50
60
D
3、某手机的电板剩余电量y毫安是使用天数x的 一次函数,如图 ,求:
y/毫安
x/天
(3)此种手机的电板最大带电量是多少?
(1)当手机使用2天时,电板的带电量是多少?
(2)当电板的电量小于200毫安时,手机至少使用了
几天?
解:(1)当手机使用2天时,
电板的带电量是600毫安。
(2)手机至少使用4天。
(3)此种手机的电板最大
带电量是1000毫安。
注意解题格式
必须规范!
4、汽车由天津驶往相距120km的北京,s(km)表示汽车离开天津的距离,t(h)表示汽车行驶的时间,s和t的关系如图所示,
(1)汽车用几小时可以从天津到达北京?汽车的速度
是多少?
(2)当汽车距北京40km时,汽车已出发了多长时间?
t
s
o
3
120
80
40
2
(2)(120-40)÷40=2(h)
因此,汽车已出发了2h。
120
解(1)汽车用3小时可以从天津到
达北京。
120÷3=40( km/h)
因此,汽车的速度是40km/h.
自学指导2(1分钟)
学生自学,教师巡视(3分钟)
1、认真自学例2;
2、完成P92做一做;
3、思考:一次函数y=kx+b与方程kx+b=0有什
么联系?
仔细阅读课本P91例2—P92的内容,思考并完成:
2、一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系?
从“形”的方面看,函数y=0.5x+1与x轴交点的横坐标,即为方程0.5x+1=0的解。
2
0
1
3
1
2
3
-1
-2
-3
-1
-2
-3
x
y
1.看图填空:(1)当y=0时,x=__;
(2)直线的函数关系式是________
2.一元一次方程0.5x+1=0的解是x= .
直线y=0.5x+1与x轴的交点坐标是 .
-2
y=0.5x+1
1、讨论课本P92“做一做”和“议一议”,解答下列问题:
(-2,0)
-2
更正、点拨(3分钟)
从“数”的方面看,当一次函数y=0.5x+1的函数值为0时,相应的自变量的值即为方程0.5x+1=0的解。
(1)排水前,蓄水池共有水______m3,
最多用_____小时排完;
(3)排水6小时后,蓄水池的剩余
水量是______,当蓄水池中只剩50m3的水
时,排水时间是____小时。
1、如图,是蓄水池的剩余水量V(m3)与排水时间t(h)之间的关系图形,请根据图象解答下列问题:
(2)每小时排水____m3 ,剩余
水量V与排水时间t的函数关
系式是___________,自变量
的取值范围是________.
400
8
50
V=-50t+400
0≤t≤8
100
t(h)
0
4
8
200
400
V(m3)
7
自学检测2:(8分钟)
4、如图,直线y=kx+b与x轴交于
点A(-4,0),则关于x的一
元一次方程kx+b=0的解
是___ .
2、方程2x-5=0的解是____ ,直线y=2x-5
与x轴的交点坐标是____ .
3、已知函数y=kx+b的图象如图所示,则方程
kx+b=0的解是( )
A.x=1 B.x=2
C.x=0 D.不能确定
x=-4
x=2.5
(2.5,0)
X
y
O
A
-4
y=kx+b
2
0
1
1
2
-1
-1
x
y
A
小结(1分钟)
注意:(1)明确坐标轴代表的实际意义。
(2)自变量的取值范围。
3、理解一元一次方程与一次函数的联系。
1、会从图象的形状、图象上点的坐标、某一量
的取值范围获取准确的信息。
2、理解图象与两坐标轴的交点坐标的实际意义。
1、某植物t天后的高度为ycm,
l反映了y与t之间的关系,
根据图象回答下列问题:
(课本P93 T2)
(1)3天后该植物高度为多少?
(2)预测植物12天后的高度;
(3)几天后该植物高度为10cm?
(4)图象对应的一次函数y=kt+b中,k和t的实际意义分
别是什么?
当堂训练(15分钟)
2
1
3
4
5
6
7
y/cm
l
1
2
3
4
5
6
7
t/天
8
9
10
0
8
9
10
解:3天后该植物高度5cm.
12天后的高度11.4cm.
10天高度为10cm
k表示增长的速度,b表示开始时的高度。
2、直线y=ax+b与x轴的交点坐标为(3,0)则方程ax+b=0的解是______;已知3x+m=0的解是x=-5,则直线y=3x+m与x轴的交点坐标是_______。
x=3
(-5,0)
3、某市自来水公司采取分段收费标准,右图反映的是每月收取水费y (元)与用水量x(吨)之间的函数关系。
(1)小明家五月份用水8吨,应交费______元;
(2)按上述收费标准,小明家三、四月份分别交水费26元和18元,四月份比三月份节约用水______吨。
X/吨
y/元
0
20
20
10
50
16
3
4、某汽车离开某城市的距离y(km)与行驶时间t(h)之间的关系式为y=kt+30,其图象如图所示:
(1)在1h至3h之间,汽车行驶的路程是多少?
(2)你能确定k的值吗?这里k的具体含义是什么?
解:(1)当t=1时,y=90;当t=3时,y=_____;
210-90=120
所以,在1时至3时之间,汽车行驶的路程是______千米
210
120
(2)把t=1,y=90代人
得K=60,K表示汽车行驶的速度。
课本P93“数学理解” T3
x/kg
o
y
/cm
20
20
10
解:(1)弹簧未挂物体时的长度
是10cm;
(2)弹簧所挂物体的最大质量是
20kg,此时弹簧的长度是20cm
选做题:5、弹簧的长度与所挂物体的质量的关系如图
所示,观察图象回答:
(1)弹簧未挂物体时的长度是多少?
(2)弹簧所挂物体的最大质量是多少?这时弹簧的长
度是多少?
(3)在弹性限度内,求出y(cm)与x(kg)的函数关系式。
(3)
6、如图4,点A的坐标为(4,0),点P在第一象限且在
直线y=-x+6上.
(1)设点P坐标为(x,y),写出△OPA的面积S与x之
间的关系式(其中P点横坐标在O与A点之间变化;
(2)当S=10时,求点P坐标;
(3)若△OPA是以OA为底边的等腰三角形,你能求出P
的坐标吗?若能,请求出坐标;若不能,请说明
理由.
(2)P点坐标为(1,5).
(3)P点坐标为(2,4).
解:(1)
(0<x≤4)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
