22.1.4 二次函数y=ax?+bx+c的图象和性质-人教版九年级数学上册课件(19张)
文档属性
| 名称 | 22.1.4 二次函数y=ax?+bx+c的图象和性质-人教版九年级数学上册课件(19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 407.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
22.1.4
二次函数y=ax?+bx+c的图象和性质(1)
河北省宁晋县第六中学
王涛
你能说出二次函数y=—x
-6x+21图像的特征吗?
2
1
2
温故知新
1、你能说出函数
的开口方向,对称轴、顶点坐标吗?
2、函数
的图象与函数
y=
的图象有什么关系?
目
标
1.能将一般式化为顶点式,掌握顶点坐标公式,对称轴的求法.
2.会画二次函数y=ax2+bx+c的图象,知道其性质。
学习目标:
预习导学
1.组长组织交流检查核对导学案,其他同学用红笔标注存在的疑问或达不成一致意见的题目。
2.组长带头解疑答惑,互帮互助
3.小组内都不能解决的问题,上传至本组黑板上或口头提出。
预习展示(一)
我们已经知道y=a(x-h)2+k的图象和性质,能否利用这些知识来讨论
的图象和性质?
问题1
怎样将
化成y=a(x-h)2+k的形式?
想一想,配方的方法及步骤是什么?
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式
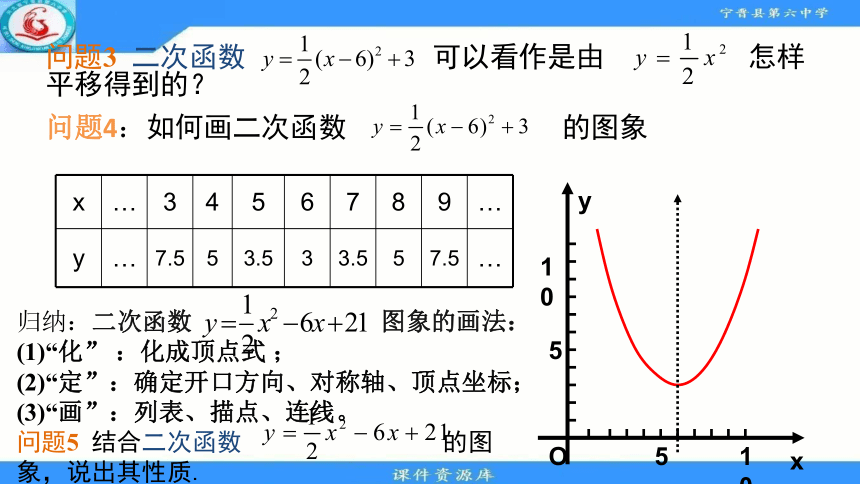
问题3
二次函数
可以看作是由
怎样平移得到的?
问题4:如何画二次函数
的图象
x
…
3
4
5
6
7
8
9
…
y
…
7.5
5
3.5
3
3.5
5
7.5
…
5
10
5
10
O
x
y
归纳:二次函数
图象的画法:
(1)“化”
:化成顶点式
;
(2)“定”:确定开口方向、对称轴、顶点坐标;
(3)“画”:列表、描点、连线。
问题5
结合二次函数
的图象,说出其性质.
配方:
提取二次项系数
配方:加上再减去一次项系数绝对值一半的平方
整理:前三项化为平方形式,后两项合并同类项
化简:去掉中括号
这个结果通常称为求顶点坐标公式.
预习展示二
思考:抛物线y=ax?+bx+c的对称轴、顶点坐标是什么?你是如何得到的?
函数y=ax?+bx+c的对称轴、顶点坐标是什么?
x
y
O
x
y
O
如果a>0,当x<
时,y随x的增大而减小;当x>
时,y随x的增大而增大.
如果a<0,当x<
时,y随x的增大而增大;
当x>
时,y随x的增大而减小.
预习自测
1、确定下列二次函数图象的对称轴和顶点坐标
2、抛物线y=2x2+bx+c的顶点坐标为(-1,2),则b=___,c=___.
互动探究
一
求抛物线y=-2x2-5x+7的对称轴和顶点坐标(用两种方法)并画出草图。
对于y=ax2+bx+c我们可以确定它的开口方向,求出它的对称轴、顶点坐标、与y轴的交点坐标、与x轴的交点坐标(有交点时),这样就可以画出它的大致图象。
1、抛物线y=x2+bx+c的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为
y=(x-1)2-4,则b、c的值为_________
変式演练1.将抛物线y=x2-6x+5向____平移____
个单位长度,则得到抛物线y=x2-6x+9.
2.将抛物线y=x2-4x+3向右平移2个单位长度后所得新的抛物线的顶点坐标为_______________
互动探究二
互动探究三
二次函数y=-x2+bx+c的图象如图所示,若点A(x1,y1),B(x2,y2)在此函数图象上,且x1<x2<1,则y1与y2的大小关
系是_____
___________。
y1<y2
已知二次函数y=ax2+bx+c的图像如图所示,有下列结论:①abc>0;②b=2a;③a+b+c<0;④a-b+c>0。其中正确的个数是(
)
互动探究四
二次函数
的图象如下图所示,请根据二次函数的性质填空:
x
y
O
x=0时,y=c
开口向上,a>0
a1
___
0,a2___
0
b1___
0,
b2___
0
c1___
0,
c2___
0
x
y
O
x=0时,y=c.
对称轴是y轴,x=0
对称轴在y轴右侧,x>0
a3___
0
b3___
0
c3___
0
a4___
0
b4___
0
c4___
0
二次函数y=ax2+bx+c的图象与a、b、c的关系
字母符号
图象的特征
a>0
开口_____________________
a<0
开口_____________________
b=0
对称轴为_____轴
a、b同号
对称轴在y轴的____侧
a、b异号
对称轴在y轴的____侧
c=0
经过原点
c>0
与y轴交于_____半轴
c<0
与y轴交于_____半轴
小
结
1.形如y=ax?+bx+c(a≠0)的二次函数的顶点坐标及对称轴的确定:
(1)当二次函数
y=ax?+bx+c
容易配方时,可采用配方法来确定顶点坐标及对称轴方程;
(2)当a,b,c比较复杂时,可直接用公式来确定:抛物线y=ax?+bx+c的对称轴为x=
,顶点坐标是
(
,
).
2.解决二次函数y=ax?+bx+c的问题时,应先将它转化为y=a(x-h)?+k形式后,再进行研究.
课堂小结:
当堂检测
必做:导测16页1、2、3(全体学生)
选做:4--9题(3号和4号)
10--12题(1号和2号)
预习安排
1.阅读课本39-40页待定系数法及例题,完成练习。
2.完成导学案31页预习导学的内容,组长下节课上课前组织校对答案,经组内讨论不能解决的问题课前把题号或疑问上传本组黑板上。
22.1.4
二次函数y=ax?+bx+c的图象和性质(1)
河北省宁晋县第六中学
王涛
你能说出二次函数y=—x
-6x+21图像的特征吗?
2
1
2
温故知新
1、你能说出函数
的开口方向,对称轴、顶点坐标吗?
2、函数
的图象与函数
y=
的图象有什么关系?
目
标
1.能将一般式化为顶点式,掌握顶点坐标公式,对称轴的求法.
2.会画二次函数y=ax2+bx+c的图象,知道其性质。
学习目标:
预习导学
1.组长组织交流检查核对导学案,其他同学用红笔标注存在的疑问或达不成一致意见的题目。
2.组长带头解疑答惑,互帮互助
3.小组内都不能解决的问题,上传至本组黑板上或口头提出。
预习展示(一)
我们已经知道y=a(x-h)2+k的图象和性质,能否利用这些知识来讨论
的图象和性质?
问题1
怎样将
化成y=a(x-h)2+k的形式?
想一想,配方的方法及步骤是什么?
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式
问题3
二次函数
可以看作是由
怎样平移得到的?
问题4:如何画二次函数
的图象
x
…
3
4
5
6
7
8
9
…
y
…
7.5
5
3.5
3
3.5
5
7.5
…
5
10
5
10
O
x
y
归纳:二次函数
图象的画法:
(1)“化”
:化成顶点式
;
(2)“定”:确定开口方向、对称轴、顶点坐标;
(3)“画”:列表、描点、连线。
问题5
结合二次函数
的图象,说出其性质.
配方:
提取二次项系数
配方:加上再减去一次项系数绝对值一半的平方
整理:前三项化为平方形式,后两项合并同类项
化简:去掉中括号
这个结果通常称为求顶点坐标公式.
预习展示二
思考:抛物线y=ax?+bx+c的对称轴、顶点坐标是什么?你是如何得到的?
函数y=ax?+bx+c的对称轴、顶点坐标是什么?
x
y
O
x
y
O
如果a>0,当x<
时,y随x的增大而减小;当x>
时,y随x的增大而增大.
如果a<0,当x<
时,y随x的增大而增大;
当x>
时,y随x的增大而减小.
预习自测
1、确定下列二次函数图象的对称轴和顶点坐标
2、抛物线y=2x2+bx+c的顶点坐标为(-1,2),则b=___,c=___.
互动探究
一
求抛物线y=-2x2-5x+7的对称轴和顶点坐标(用两种方法)并画出草图。
对于y=ax2+bx+c我们可以确定它的开口方向,求出它的对称轴、顶点坐标、与y轴的交点坐标、与x轴的交点坐标(有交点时),这样就可以画出它的大致图象。
1、抛物线y=x2+bx+c的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为
y=(x-1)2-4,则b、c的值为_________
変式演练1.将抛物线y=x2-6x+5向____平移____
个单位长度,则得到抛物线y=x2-6x+9.
2.将抛物线y=x2-4x+3向右平移2个单位长度后所得新的抛物线的顶点坐标为_______________
互动探究二
互动探究三
二次函数y=-x2+bx+c的图象如图所示,若点A(x1,y1),B(x2,y2)在此函数图象上,且x1<x2<1,则y1与y2的大小关
系是_____
___________。
y1<y2
已知二次函数y=ax2+bx+c的图像如图所示,有下列结论:①abc>0;②b=2a;③a+b+c<0;④a-b+c>0。其中正确的个数是(
)
互动探究四
二次函数
的图象如下图所示,请根据二次函数的性质填空:
x
y
O
x=0时,y=c
开口向上,a>0
a1
___
0,a2___
0
b1___
0,
b2___
0
c1___
0,
c2___
0
x
y
O
x=0时,y=c.
对称轴是y轴,x=0
对称轴在y轴右侧,x>0
a3___
0
b3___
0
c3___
0
a4___
0
b4___
0
c4___
0
二次函数y=ax2+bx+c的图象与a、b、c的关系
字母符号
图象的特征
a>0
开口_____________________
a<0
开口_____________________
b=0
对称轴为_____轴
a、b同号
对称轴在y轴的____侧
a、b异号
对称轴在y轴的____侧
c=0
经过原点
c>0
与y轴交于_____半轴
c<0
与y轴交于_____半轴
小
结
1.形如y=ax?+bx+c(a≠0)的二次函数的顶点坐标及对称轴的确定:
(1)当二次函数
y=ax?+bx+c
容易配方时,可采用配方法来确定顶点坐标及对称轴方程;
(2)当a,b,c比较复杂时,可直接用公式来确定:抛物线y=ax?+bx+c的对称轴为x=
,顶点坐标是
(
,
).
2.解决二次函数y=ax?+bx+c的问题时,应先将它转化为y=a(x-h)?+k形式后,再进行研究.
课堂小结:
当堂检测
必做:导测16页1、2、3(全体学生)
选做:4--9题(3号和4号)
10--12题(1号和2号)
预习安排
1.阅读课本39-40页待定系数法及例题,完成练习。
2.完成导学案31页预习导学的内容,组长下节课上课前组织校对答案,经组内讨论不能解决的问题课前把题号或疑问上传本组黑板上。
同课章节目录
