22.3实际问题与二次函数(2)-人教版九年级数学上册课件(24张)
文档属性
| 名称 | 22.3实际问题与二次函数(2)-人教版九年级数学上册课件(24张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 186.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 13:55:05 | ||
图片预览







文档简介
22.3.2实际问题与二次函数--利润问题
温故知新
单件利润=售价 - 进价
销售额= 售价×销售量
总利润=销售额- 总成本=单件利润×销售量
2.已知二次函数y=-10x2+100x+6000,当x为何值时,y有最大值,最大值是多少?
1、已知某商品的进价为每件40元,售价是每件60元,每星期可卖出300件。那么一周的利润是多少?
学习目标
1.能将现实生活中的利润问题转化为二次函数问题及确定自变量的取值范围;
2.会利用二次函数的“最值”求利润问题中的最值.
1.当每件涨价x元时,售价为( )元,每周少卖出( )件。
2.实际卖出( )件,销售额为( )元。
3.买进商品需付( )元。
4.故,总利润( )元。
60+x
10x
300-10x
(60+x)(300-10x)
40(300-10x)
(60+x)(300-10x)-40(300-10x)
预习展示
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
涨价销售①每件涨价x元,则每星期售出商品的利润y元,填空:
②自变量x的取值范围如何确定?
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤30.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+100x+6000,
即定价65元时,最大利润是6250元.
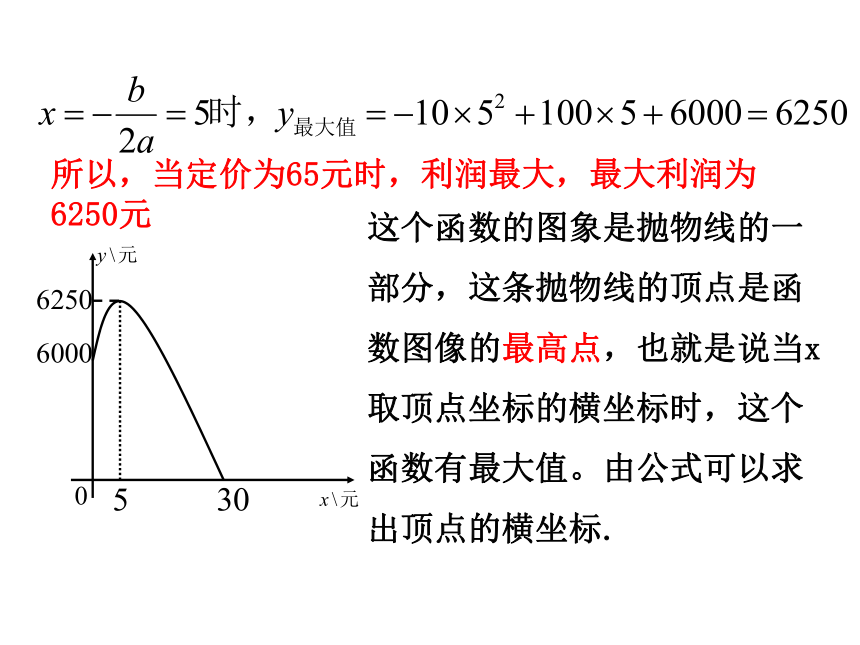
当 时,
y最大= -10×52+100×5+6000=6250.
所以,当定价为65元时,利润最大,最大利润为6250元
这个函数的图象是抛物线的一部分,这条抛物线的顶点是函数图像的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值。由公式可以求出顶点的横坐标.
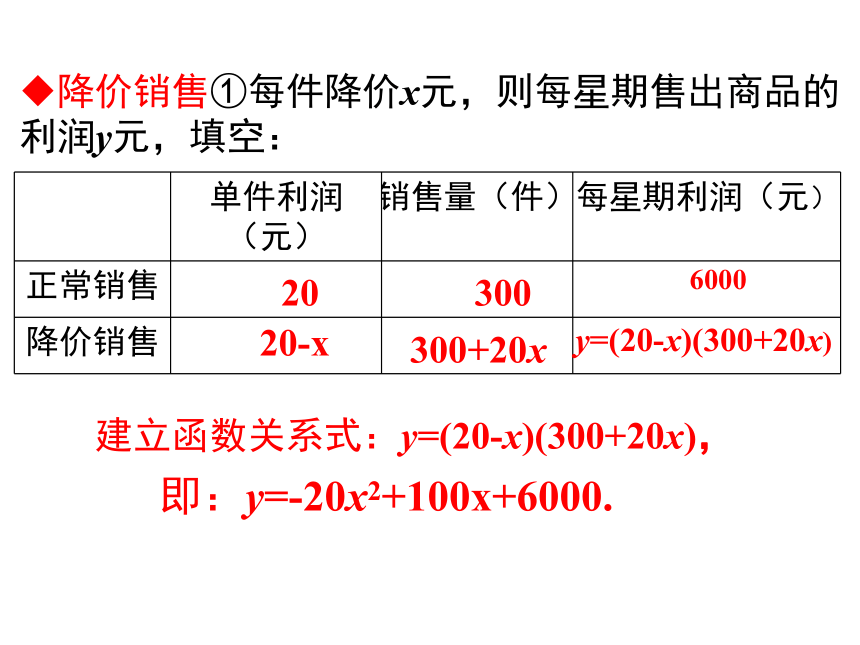
降价销售①每件降价x元,则每星期售出商品的利润y元,填空:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单件利润(元)
销售量(件)
每星期利润(元)
正常销售
降价销售
20
300
20-x
300+20x
y=(20-x)(300+20x)
建立函数关系式:y=(20-x)(300+20x),
即:y=-20x2+100x+6000.
6000
综合可知,应定价65元时,才能使利润最大。
②自变量x的取值范围如何确定?
营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤20.
③涨价多少元时,利润最大,是多少?
?
归纳总结
利用二次函数解决最大利润问题的一般步骤:
1.设 自变量写出函数解析式
2.结合实际意义,确定自变量的取值范围
3.在自变量的取值范围内确定最大利润:根据顶点公式或配方法,也可以画出函数的简图,利用简图和性质求出最大值或最小值
预习自测
某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件。根据销售经验,提高单价会导致销售量的减少,即销售单价每提高2元,销售量相应减少20件,则售价提高多少元时,才能在半个月内获得最大利润?
互动探究1
进价为80元的某件定价100元时,每月可卖2000件,价格每上涨2元,销售量便减少10件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为 .
每月利润w(元)与衬衣售价x(元)之间的函数关系为 。并求x为何值时,w最大?
注意x有时表示的是涨价或降价,有时表示是售价
由实际问题转化为函数问题很关键
解:∵y=-n 2 +15n-36=0,
∴n 2 -15n+36=0,
∴n 1 =3,n 2 =12,
∵a=-1<0,
∴抛物线开口向下,
∴n=1和n=2时,y<0,
∴该企业一年中应停产的月份是1月,2月,3月,12月.
互动探究2
生产季节性产品的企业,当它的产品无利润时就会及时停产,现有一生产季节性产品的企业,一年中获得利润y与月份n之间的函数关系式是y=-n 2 +15n-36,那么该企业一年中应停产的月份是( )
A.1月,2月 B.1月,2月,3月
C.3月,12月 D.1月,2月,3月,12月
合作探究3
某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:
y=-2x+80.设这种产品每天的销售利润为w元。
(1)w与x之间的函数解析式。写出x的取值范围
w=(x﹣20)y=(x﹣20)(﹣2x+80)
=﹣2x?2?+120x﹣1600,
由题意,有 ?,
解得20≤x≤40.
由题意,有 ?,
解得20≤x≤40.
解得20≤x≤40.
由题意,有
(2) 该产品定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
∵w=﹣2x?2?+120x﹣1600=﹣2(x﹣30)?2?+200,
∴当x=30时,w有最大值200.
故当销售价定为30元/千克时,每天可获最大销售利润200元;
(3)如果物价部门规定这种产品的销售价不高于28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
当w=150时,可得方程﹣2x?2?+120x﹣1600=150,
整理,得x?2?﹣60x+875=0,
解得x?1?=25,x?2?=35.
∵物价部门规定这种产品的销售价不得高于28元/千克,∴x?2?=35不合题意,应舍去.
变式
1、若每天获得不低于150元的销售利润,销售定价应定为每千克多少元?
x
W
150
25
35
由图象知,25≤x≤35
当w=150时,﹣2x?2?+120x﹣1600=150,
解得x?1?=25,x?2?=35.
变式
2、若销售单价不高于28元/千克,求最大销售利润?
x
W
28
20
30
∵当20≤x≤28时
W随x的增大而增大
∴当x = 28时,W最大= 192
注意:在实际问题中必须考虑自变量的取值范围内是否包含顶点,
顶点是二次函数的最值,不一定是实际问题的最值
变式
x
W
27
35
30
3、若销售单价不高于35元/千克,不低于27元/千克,求销售利润最小值?
当x=35时 ,W最小= 150
有时利用图象观察更简单
(2)当售价在50~70元时,每月销售量与售价的关系如图所示,则此时当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:当50≤x≤70时,
设y与x函数关系式为y=kx+b,
∵线段过(50,60)和(70,20).
50k+b=60
70k+b=20
∴
∴y =-2x +160(50≤x≤70)
解得:
k =-2
b = 160
某商店试销一种新商品,新商品的进价为30元/件,经过一段时间的试销发现,每月的销售量会因售价的调整而不同.令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
(1)当售价在40~50元时,每月销售量都为60件,则此时每月的总利润最多是多少元?
解:由题意得:当40≤x≤50时,
Q = 60(x-30)= 60x-1800
∵ y = 60 > 0,Q随x的增大而增大
∴当x最大= 50时,Q最大= 1200
答:此时每月的总利润最多是1200元.
能力提升
∴y =-2x +160(50≤x≤70)
∴Q=(x-30)y
=(x-30)(-2x + 160)
=-2x2 + 220x- 4800
=-2(x-55)2 +1250 (50≤x≤70)
∵a = -2<0,图象开口向下,
∴当x = 55时,Q最大= 1250
∴当售价在50~70元时,售价x是55元时,获利最大,
最大利润是1250元.
②当50≤x≤70时,
令Q = 1218,得
-2(x-55)2 +1250=1218
解得:x1=51,x2=59
由图象和性质可知:
当51≤x≤59时,Q≥1218
x
Q
0
55
1218
59
51
1250
(3)若该商店销售该商品所获利润不低于1218元,试确定该商品的售价x的取值范围;
解:①当40≤x≤50时,
∵Q最大= 1200<1218,
∴此情况不存在.
(4)在(3)的条件下,已知该商店采购这种新商品的进货款不低于1620元,则售价x为多少元时,利润最大,最大利润是多少元?
解:由题意得:
51≤x≤59
30 (-2 x +160)≥1620
解得:51≤x≤53
∵Q=-2(x-55)2 +1250的顶点
不在51≤x≤53范围内,
又∵a =-2<0,
∴当51≤x≤53时 ,
Q随x的增大而增大
∴当x最大 = 53时,Q最大= 1242
∴此时售价x应定为53元,
利润最大,最大利润是1242元.
x
Q
0
55
1242
53
51
最大利润问题
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降件:要保证单件利润≥0.
确定最大利润
利用配方法或公式求最大值或利用函数简图和性质求出.
课堂小结
思想方法:建模思想。建立函数关系,用函数的观点、思想去分析实际问题。
当堂检测
导学测评第22页
必做:第1,2,3, 6题
选做:第4, 5题
温故知新
单件利润=售价 - 进价
销售额= 售价×销售量
总利润=销售额- 总成本=单件利润×销售量
2.已知二次函数y=-10x2+100x+6000,当x为何值时,y有最大值,最大值是多少?
1、已知某商品的进价为每件40元,售价是每件60元,每星期可卖出300件。那么一周的利润是多少?
学习目标
1.能将现实生活中的利润问题转化为二次函数问题及确定自变量的取值范围;
2.会利用二次函数的“最值”求利润问题中的最值.
1.当每件涨价x元时,售价为( )元,每周少卖出( )件。
2.实际卖出( )件,销售额为( )元。
3.买进商品需付( )元。
4.故,总利润( )元。
60+x
10x
300-10x
(60+x)(300-10x)
40(300-10x)
(60+x)(300-10x)-40(300-10x)
预习展示
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
涨价销售①每件涨价x元,则每星期售出商品的利润y元,填空:
②自变量x的取值范围如何确定?
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤30.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+100x+6000,
即定价65元时,最大利润是6250元.
当 时,
y最大= -10×52+100×5+6000=6250.
所以,当定价为65元时,利润最大,最大利润为6250元
这个函数的图象是抛物线的一部分,这条抛物线的顶点是函数图像的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值。由公式可以求出顶点的横坐标.
降价销售①每件降价x元,则每星期售出商品的利润y元,填空:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单件利润(元)
销售量(件)
每星期利润(元)
正常销售
降价销售
20
300
20-x
300+20x
y=(20-x)(300+20x)
建立函数关系式:y=(20-x)(300+20x),
即:y=-20x2+100x+6000.
6000
综合可知,应定价65元时,才能使利润最大。
②自变量x的取值范围如何确定?
营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤20.
③涨价多少元时,利润最大,是多少?
?
归纳总结
利用二次函数解决最大利润问题的一般步骤:
1.设 自变量写出函数解析式
2.结合实际意义,确定自变量的取值范围
3.在自变量的取值范围内确定最大利润:根据顶点公式或配方法,也可以画出函数的简图,利用简图和性质求出最大值或最小值
预习自测
某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件。根据销售经验,提高单价会导致销售量的减少,即销售单价每提高2元,销售量相应减少20件,则售价提高多少元时,才能在半个月内获得最大利润?
互动探究1
进价为80元的某件定价100元时,每月可卖2000件,价格每上涨2元,销售量便减少10件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为 .
每月利润w(元)与衬衣售价x(元)之间的函数关系为 。并求x为何值时,w最大?
注意x有时表示的是涨价或降价,有时表示是售价
由实际问题转化为函数问题很关键
解:∵y=-n 2 +15n-36=0,
∴n 2 -15n+36=0,
∴n 1 =3,n 2 =12,
∵a=-1<0,
∴抛物线开口向下,
∴n=1和n=2时,y<0,
∴该企业一年中应停产的月份是1月,2月,3月,12月.
互动探究2
生产季节性产品的企业,当它的产品无利润时就会及时停产,现有一生产季节性产品的企业,一年中获得利润y与月份n之间的函数关系式是y=-n 2 +15n-36,那么该企业一年中应停产的月份是( )
A.1月,2月 B.1月,2月,3月
C.3月,12月 D.1月,2月,3月,12月
合作探究3
某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:
y=-2x+80.设这种产品每天的销售利润为w元。
(1)w与x之间的函数解析式。写出x的取值范围
w=(x﹣20)y=(x﹣20)(﹣2x+80)
=﹣2x?2?+120x﹣1600,
由题意,有 ?,
解得20≤x≤40.
由题意,有 ?,
解得20≤x≤40.
解得20≤x≤40.
由题意,有
(2) 该产品定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
∵w=﹣2x?2?+120x﹣1600=﹣2(x﹣30)?2?+200,
∴当x=30时,w有最大值200.
故当销售价定为30元/千克时,每天可获最大销售利润200元;
(3)如果物价部门规定这种产品的销售价不高于28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
当w=150时,可得方程﹣2x?2?+120x﹣1600=150,
整理,得x?2?﹣60x+875=0,
解得x?1?=25,x?2?=35.
∵物价部门规定这种产品的销售价不得高于28元/千克,∴x?2?=35不合题意,应舍去.
变式
1、若每天获得不低于150元的销售利润,销售定价应定为每千克多少元?
x
W
150
25
35
由图象知,25≤x≤35
当w=150时,﹣2x?2?+120x﹣1600=150,
解得x?1?=25,x?2?=35.
变式
2、若销售单价不高于28元/千克,求最大销售利润?
x
W
28
20
30
∵当20≤x≤28时
W随x的增大而增大
∴当x = 28时,W最大= 192
注意:在实际问题中必须考虑自变量的取值范围内是否包含顶点,
顶点是二次函数的最值,不一定是实际问题的最值
变式
x
W
27
35
30
3、若销售单价不高于35元/千克,不低于27元/千克,求销售利润最小值?
当x=35时 ,W最小= 150
有时利用图象观察更简单
(2)当售价在50~70元时,每月销售量与售价的关系如图所示,则此时当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:当50≤x≤70时,
设y与x函数关系式为y=kx+b,
∵线段过(50,60)和(70,20).
50k+b=60
70k+b=20
∴
∴y =-2x +160(50≤x≤70)
解得:
k =-2
b = 160
某商店试销一种新商品,新商品的进价为30元/件,经过一段时间的试销发现,每月的销售量会因售价的调整而不同.令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
(1)当售价在40~50元时,每月销售量都为60件,则此时每月的总利润最多是多少元?
解:由题意得:当40≤x≤50时,
Q = 60(x-30)= 60x-1800
∵ y = 60 > 0,Q随x的增大而增大
∴当x最大= 50时,Q最大= 1200
答:此时每月的总利润最多是1200元.
能力提升
∴y =-2x +160(50≤x≤70)
∴Q=(x-30)y
=(x-30)(-2x + 160)
=-2x2 + 220x- 4800
=-2(x-55)2 +1250 (50≤x≤70)
∵a = -2<0,图象开口向下,
∴当x = 55时,Q最大= 1250
∴当售价在50~70元时,售价x是55元时,获利最大,
最大利润是1250元.
②当50≤x≤70时,
令Q = 1218,得
-2(x-55)2 +1250=1218
解得:x1=51,x2=59
由图象和性质可知:
当51≤x≤59时,Q≥1218
x
Q
0
55
1218
59
51
1250
(3)若该商店销售该商品所获利润不低于1218元,试确定该商品的售价x的取值范围;
解:①当40≤x≤50时,
∵Q最大= 1200<1218,
∴此情况不存在.
(4)在(3)的条件下,已知该商店采购这种新商品的进货款不低于1620元,则售价x为多少元时,利润最大,最大利润是多少元?
解:由题意得:
51≤x≤59
30 (-2 x +160)≥1620
解得:51≤x≤53
∵Q=-2(x-55)2 +1250的顶点
不在51≤x≤53范围内,
又∵a =-2<0,
∴当51≤x≤53时 ,
Q随x的增大而增大
∴当x最大 = 53时,Q最大= 1242
∴此时售价x应定为53元,
利润最大,最大利润是1242元.
x
Q
0
55
1242
53
51
最大利润问题
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降件:要保证单件利润≥0.
确定最大利润
利用配方法或公式求最大值或利用函数简图和性质求出.
课堂小结
思想方法:建模思想。建立函数关系,用函数的观点、思想去分析实际问题。
当堂检测
导学测评第22页
必做:第1,2,3, 6题
选做:第4, 5题
同课章节目录
