23.1成比例线段(2)平行线分线段成比例-华东师大版九年级数学上册课件(14张)
文档属性
| 名称 | 23.1成比例线段(2)平行线分线段成比例-华东师大版九年级数学上册课件(14张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 443.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 13:57:29 | ||
图片预览


文档简介
§23.1 成比例线段(2)
——平行线分线段成比例
知识探索
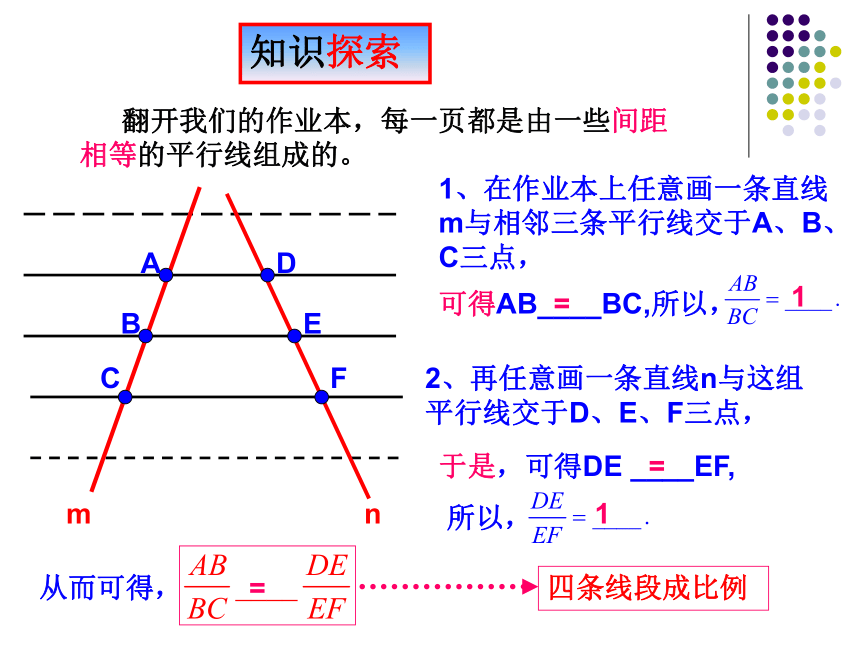
翻开我们的作业本,每一页都是由一些间距相等的平行线组成的。
A
C
B
m
1、在作业本上任意画一条直线m与相邻三条平行线交于A、B、C三点,
可得AB____BC,所以,
=
1
2、再任意画一条直线n与这组平行线交于D、E、F三点,
n
D
E
F
于是,可得DE ____EF,
所以,
=
1
从而可得,
=
四条线段成比例
问题
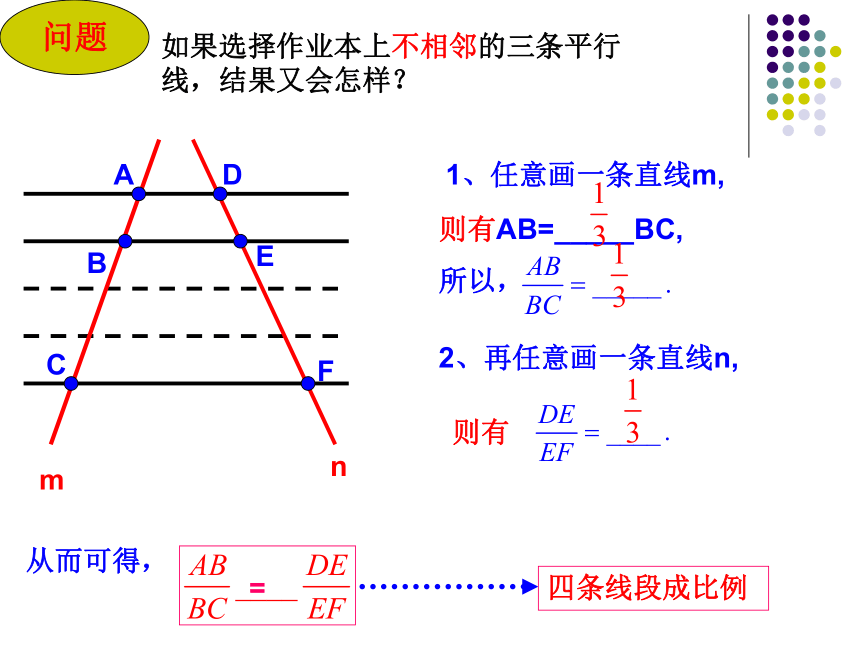
如果选择作业本上不相邻的三条平行线,结果又会怎样?
1、任意画一条直线m,
m
A
B
C
则有AB=_____BC,
所以,
2、再任意画一条直线n,
n
D
E
F
则有
从而可得,
=
四条线段成比例
m
A
B
C
n
D
E
F
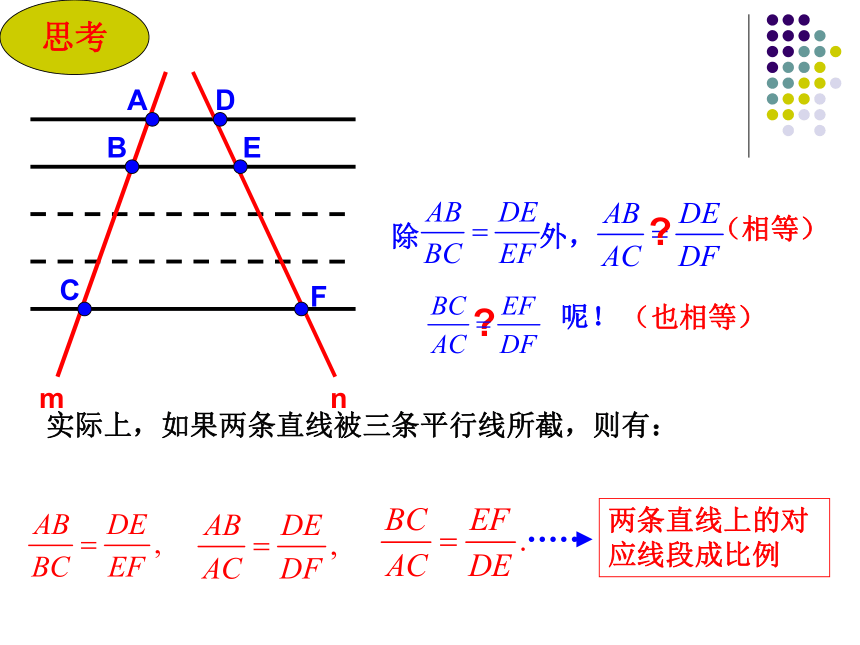
思考
除 外,
?
(相等)
(也相等)
?
呢!
实际上,如果两条直线被三条平行线所截,则有:
两条直线上的对应线段成比例
知识概括
n
m
C
E
F
A
D
B
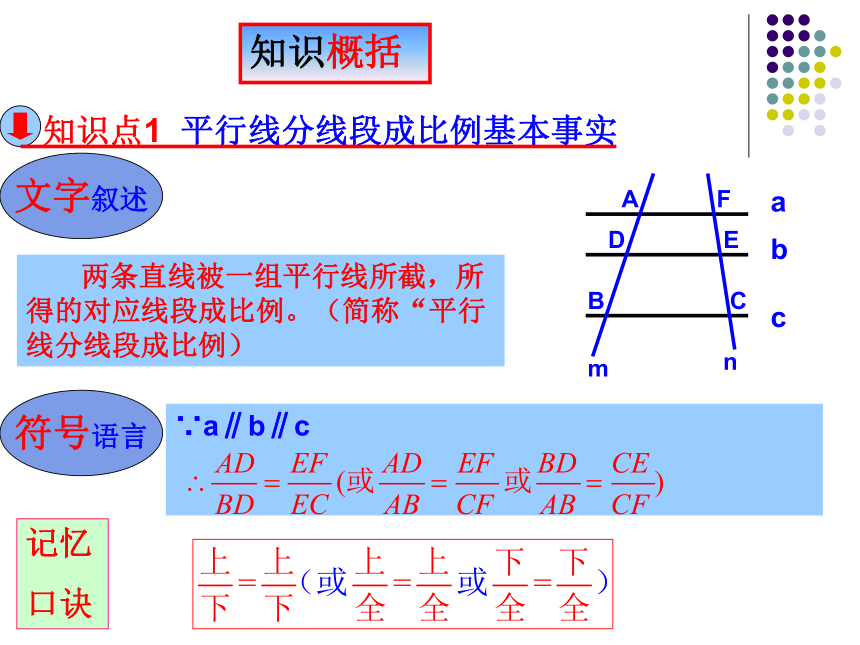
知识点1 平行线分线段成比例基本事实
两条直线被一组平行线所截,所得的对应线段成比例。(简称“平行线分线段成比例)
文字叙述
a
b
c
符号语言
∵a∥b∥c
记忆
口诀
例题解析
例1
F
E
D
A
B
C
如图, ,AB=4,
DE=3,EF=6.求BC的长。
分析:
找准对应线段,正确列出比例式
DE
AB
_______
BC
_______
EF
【解】
( )
平行线分线段成比例
∵AB=4,DE=3,EF=6
∴BC=8
课本P53例题
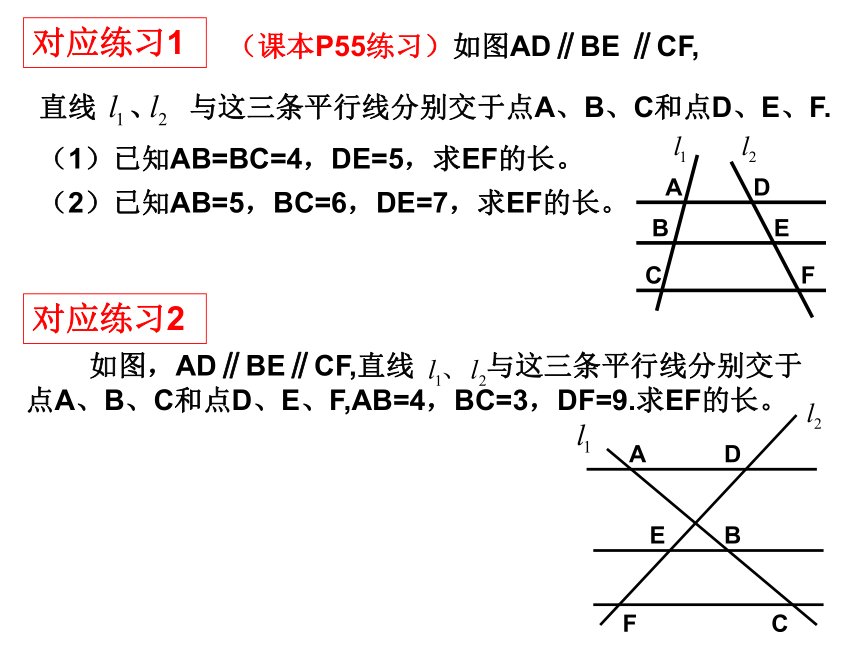
对应练习1
(课本P55练习)如图AD∥BE ∥CF,
直线 、 与这三条平行线分别交于点A、B、C和点D、E、F.
(1)已知AB=BC=4,DE=5,求EF的长。
F
E
D
A
B
C
(2)已知AB=5,BC=6,DE=7,求EF的长。
对应练习2
如图,AD∥BE∥CF,直线 与这三条平行线分别交于点A、B、C和点D、E、F,AB=4,BC=3,DF=9.求EF的长。
F
A
B
C
D
E
学法
指导
平行线分线段成比例两种图式:
A
D
B
①
F
E
C
A
D
B
②
F
E
C
同样有对应线段成比例,即
知识探索
A
D
B
F
E
C
A
D
B
F
E
C
思考1
将右边直线平行移动,使得点F与点A重合。两条直线上的对应线段成比例吗?
D
A
E
B
C
去掉△ABC周围部分
可视为:DE截△ABC的两边AB、AC所得线段对应成比例
D
A
B
E
C
F
思考2
将右边直线平行移动,使得点F与点A重合。两条直线上的对应线段成比例吗?
D
A
B
E
F
C
去掉△ABC周围部分
C
D
E
A
B
可视为:DE截△ABC的两边AB、AC的延长线所得线段对应成比例
知识概括
知识点2 平行线分线段成比例基本事实推论
文字叙述
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
符号语言
∵DE∥BC
例题解析
E
F
D
C
O
B
A
例2
如图,E为 ABCD的边CD的延长线
上一点,连结BE,交AD于点F,
求证:
分析:
___∥___
AF
BC
___∥___
AB
CE
【证明】
∵AF∥BC
(平行线分线段成比例)
∵AB∥CE
(平行线分线段成比例)
对应练习3
(课本P53做一做)
如图,DE∥AF∥BC,找出图中成比例的线段,写出比例式。
课堂小结
1、平行线分线段成比例基本事实:
两条直线被一组平行线所截,所得的对应线段成比例。(简称“平行线分线段成比例)
2、平行线分线段成比例基本事实推论:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
——平行线分线段成比例
知识探索
翻开我们的作业本,每一页都是由一些间距相等的平行线组成的。
A
C
B
m
1、在作业本上任意画一条直线m与相邻三条平行线交于A、B、C三点,
可得AB____BC,所以,
=
1
2、再任意画一条直线n与这组平行线交于D、E、F三点,
n
D
E
F
于是,可得DE ____EF,
所以,
=
1
从而可得,
=
四条线段成比例
问题
如果选择作业本上不相邻的三条平行线,结果又会怎样?
1、任意画一条直线m,
m
A
B
C
则有AB=_____BC,
所以,
2、再任意画一条直线n,
n
D
E
F
则有
从而可得,
=
四条线段成比例
m
A
B
C
n
D
E
F
思考
除 外,
?
(相等)
(也相等)
?
呢!
实际上,如果两条直线被三条平行线所截,则有:
两条直线上的对应线段成比例
知识概括
n
m
C
E
F
A
D
B
知识点1 平行线分线段成比例基本事实
两条直线被一组平行线所截,所得的对应线段成比例。(简称“平行线分线段成比例)
文字叙述
a
b
c
符号语言
∵a∥b∥c
记忆
口诀
例题解析
例1
F
E
D
A
B
C
如图, ,AB=4,
DE=3,EF=6.求BC的长。
分析:
找准对应线段,正确列出比例式
DE
AB
_______
BC
_______
EF
【解】
( )
平行线分线段成比例
∵AB=4,DE=3,EF=6
∴BC=8
课本P53例题
对应练习1
(课本P55练习)如图AD∥BE ∥CF,
直线 、 与这三条平行线分别交于点A、B、C和点D、E、F.
(1)已知AB=BC=4,DE=5,求EF的长。
F
E
D
A
B
C
(2)已知AB=5,BC=6,DE=7,求EF的长。
对应练习2
如图,AD∥BE∥CF,直线 与这三条平行线分别交于点A、B、C和点D、E、F,AB=4,BC=3,DF=9.求EF的长。
F
A
B
C
D
E
学法
指导
平行线分线段成比例两种图式:
A
D
B
①
F
E
C
A
D
B
②
F
E
C
同样有对应线段成比例,即
知识探索
A
D
B
F
E
C
A
D
B
F
E
C
思考1
将右边直线平行移动,使得点F与点A重合。两条直线上的对应线段成比例吗?
D
A
E
B
C
去掉△ABC周围部分
可视为:DE截△ABC的两边AB、AC所得线段对应成比例
D
A
B
E
C
F
思考2
将右边直线平行移动,使得点F与点A重合。两条直线上的对应线段成比例吗?
D
A
B
E
F
C
去掉△ABC周围部分
C
D
E
A
B
可视为:DE截△ABC的两边AB、AC的延长线所得线段对应成比例
知识概括
知识点2 平行线分线段成比例基本事实推论
文字叙述
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
符号语言
∵DE∥BC
例题解析
E
F
D
C
O
B
A
例2
如图,E为 ABCD的边CD的延长线
上一点,连结BE,交AD于点F,
求证:
分析:
___∥___
AF
BC
___∥___
AB
CE
【证明】
∵AF∥BC
(平行线分线段成比例)
∵AB∥CE
(平行线分线段成比例)
对应练习3
(课本P53做一做)
如图,DE∥AF∥BC,找出图中成比例的线段,写出比例式。
课堂小结
1、平行线分线段成比例基本事实:
两条直线被一组平行线所截,所得的对应线段成比例。(简称“平行线分线段成比例)
2、平行线分线段成比例基本事实推论:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
