23.1图形的旋转(1)-人教版九年级数学上册课件(17张)
文档属性
| 名称 | 23.1图形的旋转(1)-人教版九年级数学上册课件(17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 291.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 13:59:20 | ||
图片预览






文档简介
(共17张PPT)
23.1 图形的旋转
第一课时旋转及其性质
学习目标
1.理解旋转及其有关概念;
2.掌握旋转的性质,能利用旋转的性质进行简单的证明。
预习导学
1、 组长组织交流检查核对导学案,其他同学用红笔标注存在的疑问或达不成一致意见的题目。
2、组长带头解疑答惑,互帮互助
3、小组内都不能解决的问题,抄写至本组黑板上或口头提出。
知识点一:旋转的有关概念
(1)上面情境中的转动现象,有什么共同的特征?
(2)钟表的指针、风车、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
预习展示
归纳总结:
(1)把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的______。
(2)旋转的三要素是______ 、______ 、______。
旋转
旋转中心
旋转方向
旋转角
D
E
A
B
F
C
O
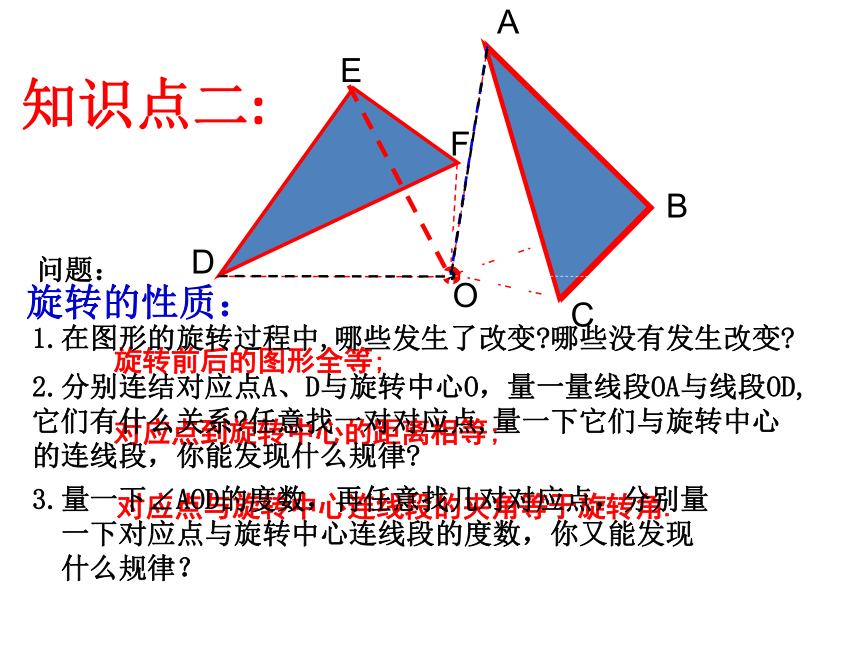
问题:
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心连线段的夹角等于旋转角.
旋转的性质:
1.在图形的旋转过程中,哪些发生了改变 哪些没有发生改变
2.分别连结对应点A、D与旋转中心O,量一量线段OA与线段OD,它们有什么关系 任意找一对对应点,量一下它们与旋转中心的连线段,你能发现什么规律
3.量一下∠AOD的度数,再任意找几对对应点,分别量
一下对应点与旋转中心连线段的度数,你又能发现
什么规律?
知识点二:
归纳总结:
旋转的性质:
1.对应点到旋转中心的距离______;
2.对应点与旋转中心所连线段的夹角等于______;
3.旋转前、后的图形______.
相等
全等
旋转角
A
B
O
C
D
点B的对应点是________;
线段OB的对应线段是________;
线段CD的对应线段是________;
∠AOB的对应角是________;
∠B的对应角是________;
旋转中心是________;
旋转角是_________________;
如图,△ABO绕点O旋转得到△CDO,则:
点D
线段OD
线段AB
∠COD
∠D
点O
∠AOC
∠BOD
预习自测
互动探究一
△OAB绕点O旋转600到△OCD的位置,点E是线段AB的中点。
(1)点E对应的点是那个点。
(2)∠AOC与∠BOD有什么关系,为什么?
E
.
关键是确定旋转三要素,找到旋转前后的对应元素,再利用旋转的性质解决问题。
合作探究二
如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连结AA1。
(1)写出旋转角的度数;
(2)求证:△A1AB是等腰三角形。
在确定旋转角时,先找对应点,再找对应点与旋转中心连线的夹角,就得到了旋转角。
已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.
变式
变式
已知,在Rt△ABC中,∠C=90°∠BAC=45°,AC=2,将△ABC绕点A顺时针旋转60°得到△ADE,连接BE,交AD于点F,求BE的长.
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形.
能力提升
课堂小结
旋转的定义:在平面内,将一个图形绕一个定点沿着某个方向转动一定的角度,这样的图形运动称为旋转. 这个定点称为旋转中心,转动的角称为旋转角.
旋转的性质:
旋转不改变图形的大小与形状,但可改变定向;
旋转前后两图形任意一对对应点与旋转中心的连线所成的角都是旋转角,
对应点到旋转中心的距离相等.
当堂检测
导学测评:必做题:1---7题
选做题:9题
预习安排
1.阅读课本61页,完成练习。
2.完成导学案45页预习导学的内容,组长下节课上课前组织校对答案,经组内讨论不能解决的问题课前把题号或疑问上传本组黑板上。
谢谢大家
23.1 图形的旋转
第一课时旋转及其性质
学习目标
1.理解旋转及其有关概念;
2.掌握旋转的性质,能利用旋转的性质进行简单的证明。
预习导学
1、 组长组织交流检查核对导学案,其他同学用红笔标注存在的疑问或达不成一致意见的题目。
2、组长带头解疑答惑,互帮互助
3、小组内都不能解决的问题,抄写至本组黑板上或口头提出。
知识点一:旋转的有关概念
(1)上面情境中的转动现象,有什么共同的特征?
(2)钟表的指针、风车、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
预习展示
归纳总结:
(1)把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的______。
(2)旋转的三要素是______ 、______ 、______。
旋转
旋转中心
旋转方向
旋转角
D
E
A
B
F
C
O
问题:
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心连线段的夹角等于旋转角.
旋转的性质:
1.在图形的旋转过程中,哪些发生了改变 哪些没有发生改变
2.分别连结对应点A、D与旋转中心O,量一量线段OA与线段OD,它们有什么关系 任意找一对对应点,量一下它们与旋转中心的连线段,你能发现什么规律
3.量一下∠AOD的度数,再任意找几对对应点,分别量
一下对应点与旋转中心连线段的度数,你又能发现
什么规律?
知识点二:
归纳总结:
旋转的性质:
1.对应点到旋转中心的距离______;
2.对应点与旋转中心所连线段的夹角等于______;
3.旋转前、后的图形______.
相等
全等
旋转角
A
B
O
C
D
点B的对应点是________;
线段OB的对应线段是________;
线段CD的对应线段是________;
∠AOB的对应角是________;
∠B的对应角是________;
旋转中心是________;
旋转角是_________________;
如图,△ABO绕点O旋转得到△CDO,则:
点D
线段OD
线段AB
∠COD
∠D
点O
∠AOC
∠BOD
预习自测
互动探究一
△OAB绕点O旋转600到△OCD的位置,点E是线段AB的中点。
(1)点E对应的点是那个点。
(2)∠AOC与∠BOD有什么关系,为什么?
E
.
关键是确定旋转三要素,找到旋转前后的对应元素,再利用旋转的性质解决问题。
合作探究二
如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连结AA1。
(1)写出旋转角的度数;
(2)求证:△A1AB是等腰三角形。
在确定旋转角时,先找对应点,再找对应点与旋转中心连线的夹角,就得到了旋转角。
已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.
变式
变式
已知,在Rt△ABC中,∠C=90°∠BAC=45°,AC=2,将△ABC绕点A顺时针旋转60°得到△ADE,连接BE,交AD于点F,求BE的长.
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形.
能力提升
课堂小结
旋转的定义:在平面内,将一个图形绕一个定点沿着某个方向转动一定的角度,这样的图形运动称为旋转. 这个定点称为旋转中心,转动的角称为旋转角.
旋转的性质:
旋转不改变图形的大小与形状,但可改变定向;
旋转前后两图形任意一对对应点与旋转中心的连线所成的角都是旋转角,
对应点到旋转中心的距离相等.
当堂检测
导学测评:必做题:1---7题
选做题:9题
预习安排
1.阅读课本61页,完成练习。
2.完成导学案45页预习导学的内容,组长下节课上课前组织校对答案,经组内讨论不能解决的问题课前把题号或疑问上传本组黑板上。
谢谢大家
同课章节目录
