23.1图形的旋转(2)-人教版九年级数学上册课件(27张)
文档属性
| 名称 | 23.1图形的旋转(2)-人教版九年级数学上册课件(27张) |  | |
| 格式 | pptx | ||
| 文件大小 | 462.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 14:00:11 | ||
图片预览



文档简介
23.1 图形的旋转(2)
旋转作图
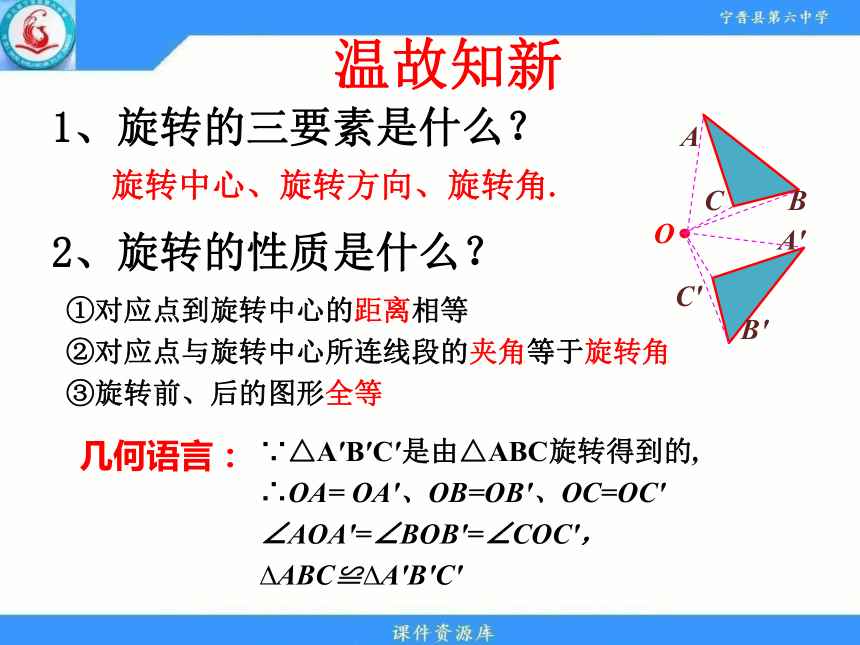
1、旋转的三要素是什么?
2、旋转的性质是什么?
①对应点到旋转中心的距离相等
②对应点与旋转中心所连线段的夹角等于旋转角
③旋转前、后的图形全等
∵△A′B′C′是由△ABC旋转得到的,
∴OA= OA′、OB=OB′、OC=OC′
∠AOA′=∠BOB′=∠COC′,?ABC≌?A′B′C′
A′
B′
C′
O
A
B
C
几何语言:
旋转中心、旋转方向、旋转角.
温故知新
学习目标
1 、会按要求做出简单平面图形旋转前后的图形,能根据给出的旋转前后的图形,确定旋转中心和旋转角。
2、体会旋转在图形变换中的作用,会利用旋转作图进行计算。
预习导学
组长组织交流预习导学,用红笔标注自己通过预学存在的问题,组长将记录各题完成情况,组织成员讨论出错题目,将未解决问题上传至本组黑板上或准备口头提出。
如无问题则进入反转环节。
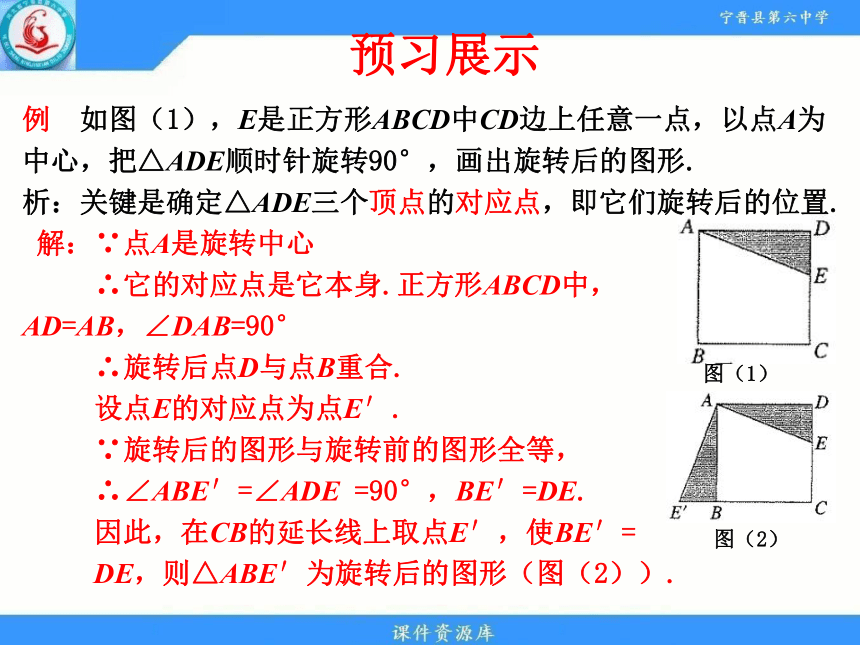
例 如图(1),E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
解:∵点A是旋转中心
∴它的对应点是它本身.正方形ABCD中,
AD=AB,∠DAB=90°
∴旋转后点D与点B重合.
设点E的对应点为点E′.
∵旋转后的图形与旋转前的图形全等,
∴∠ABE′=∠ADE =90°,BE′=DE.
因此,在CB的延长线上取点E′,使BE′=
DE,则△ABE′为旋转后的图形(图(2)).
图(1)
图(2)
预习展示
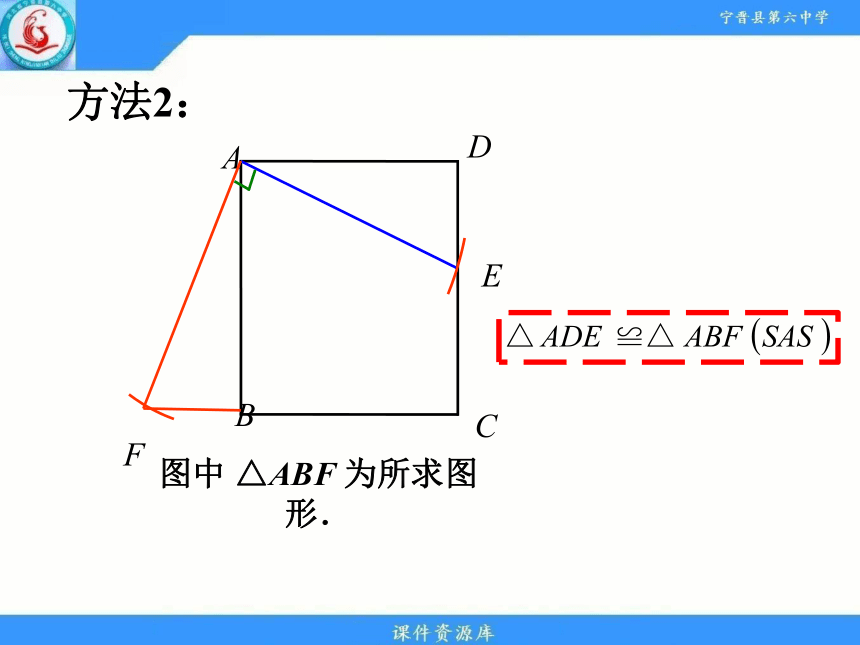
方法2:
F
图中 △ABF 为所求图形.
A
B
C
E
D
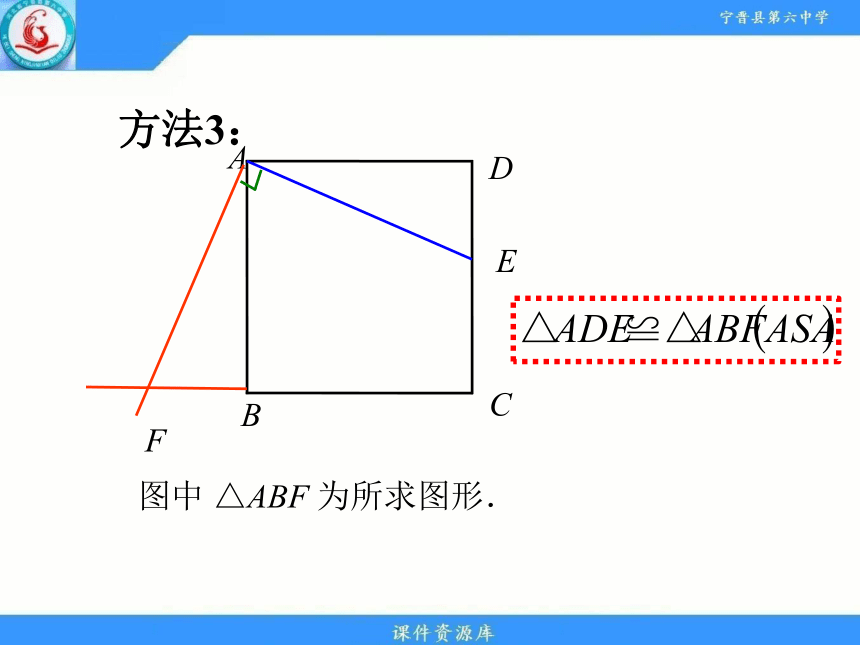
方法3:
F
图中 △ABF 为所求图形.
A
B
C
E
D
A
O
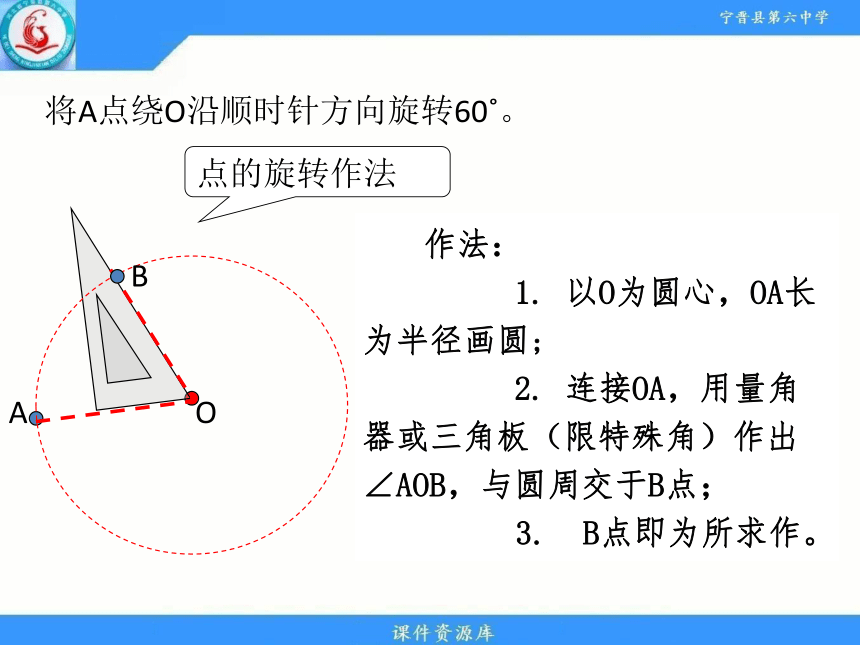
将A点绕O沿顺时针方向旋转60?。
作法:
1. 以O为圆心,OA长为半径画圆;
2. 连接OA,用量角器或三角板(限特殊角)作出∠AOB,与圆周交于B点;
3. B点即为所求作。
B
点的旋转作法
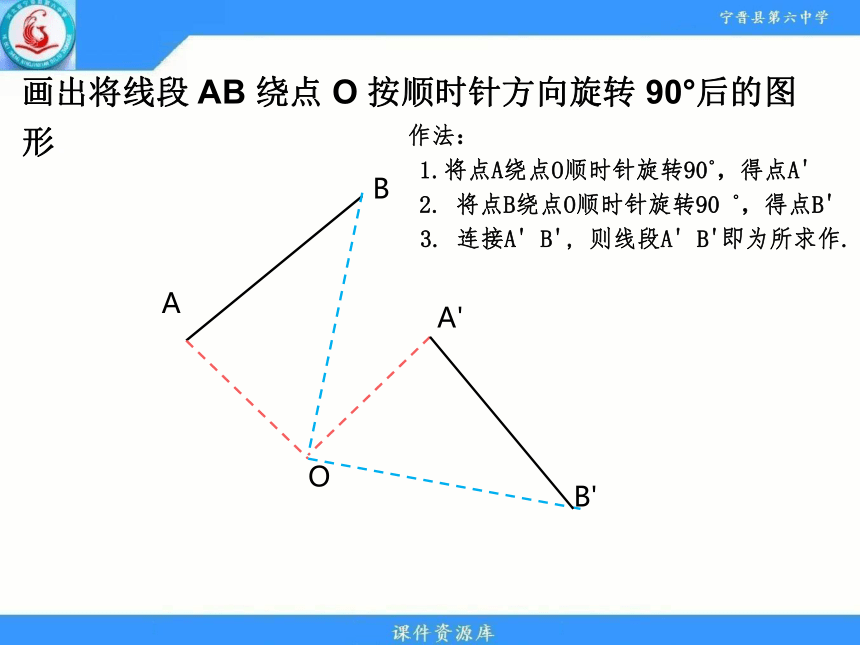
画出将线段 AB 绕点 O 按顺时针方向旋转 90°后的图形.
A
B
?
O
A'
B'
作法:
1.将点A绕点O顺时针旋转90?,得点A'
2. 将点B绕点O顺时针旋转90 ?,得点B'
3. 连接A' B', 则线段A' B'即为所求作.
已知△OAB,画出△OAB绕点O逆时针旋转100°后的图形。
B
A
O
A′
B′
1. 作∠AOC=100°,在OC上截取OA′=OA 。
2. 作∠BOD=100°,
在OD上截OB′=OB 。
C
D
注:作旋转后的图形可以转化为作旋转后的对应点。
3. 连接A′B′,则△OA′B′即为所求作。
作法:
归纳总结:旋转作图的步骤
(1)确定旋转 ,旋转 ,旋转 ;
(2)找出图形的关键点;
(3)做出关键点经旋转后的 点;
(4)按图形的顺序依次连接 点,得到旋转后的图形;
(5)写出结论。
中心
角
方向
对应
对应
旋转作图的依据是旋转的 。
性质
12
1.下列图形中,不能由其中一个图形通过旋转而构成的是( )
2.如图所示的图案中,可以由
一个“基本图案”连续旋转45°
得到的图案有 .(填序号)
C
(2)
预习自测
3、等边三角形绕它的中心旋转多少度能与自身重合?正方形呢?正n边形呢?
A/
B/
C/
任意画一个△ABC,以AC中点为中心,把这个三角形旋转180°
预习自测
在Rt△ABC中,∠B=90°,AB=3,,BC=4,请以点A为旋转中心将△ABC逆时针旋转90°。
(1)作出旋转后的图形;
(2)点C的对应点为C ′,求CC ′的长.
B
A
C
C′
B′
互动探究一
利用勾股定理和旋转的性质
变式
如图,△ABC绕点O旋转后,顶点A的对应点为点D,试确定顶点B、C对应点的位置,以及旋转后的三角形.
先将对应点与旋转中心连接,确定旋转方向和旋转角,在此基础上,分别找到各个关键点的对应点所在的射线,然后利用对应点到旋转中心的距离相等来确定对应点的具体位置
已知旋转中心和一对对应点作旋转后的图形的方法:
下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°, 你能画出△OAB 旋转后的图形 △O A ′ B ′ 吗?
A
B
O
A'
B'
互动探究二
网格中旋转90°的画法
归纳:
1.确定关键点与旋转中心所在的矩形.
2.搞清楚是顺时针还是逆时针,旋转矩形,确定对应点.
3.确定旋转后的图形.
如图,在方格纸上建立的平面直角坐标系中,将△ABO绕点O按顺时针方向旋转90°,得到△A1B1O,那么点A1的坐标为( )
变式
(2018?中考)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°
后得到△A2B2C2,请画出△A2B2C2;
变式
A
B
C
D
E
F
ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心.
.
O
确定旋转中心的步骤:
互动探究三
1.连接两组对应点.
2.作对应点连线的垂直平分线.
3.交点就是旋转中心.
变式
在如图所示的4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△ M1N1P1,则其旋转中心是 ,旋转度数是
归纳总结:1、在网格中确定旋转中心,可利
用 ,在所给的点中找到与各对对应点距
离 的点即可。
2、连接两对对应点,分别作出这两条连线的垂直平分线,交点即为旋转中心
如图,△ADE可由△CAB旋转而成,点B的对应点是E,点A的对应点是D,在平面直角坐标系中,三点坐标为A(1,0)、B(3,0)、C(1,4).
请找出旋转中心P的位置,并写出P的坐标和旋转角度
A
B
O
C
D
E
x
y
P(3,2)
变式
如图,点E是正方形ABCD内一点,连接AE、BE、CE,,若AE=1,BE=2,CE=3,则求∠BEA的度数.
解析:将△ABE绕点B顺时针旋转90°到△CBE′的位置,连接EE′,
由旋转性质知BE=BE′=2,∠EBE′=90°,
∴∠BE'E=45°,则根据勾股定理,得
在△EE′C中,E′C=1,EC=3,
EE′=????????
?
EE′=????????
?
由勾股定理逆定理可知∠EE′C=90°,
∴∠BE′C=∠BE′E+∠EE′C=135°.
互动探究四
能力提升
探究问题:
(1)方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF。
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上,
∵∠EAF=45°,
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°,
∵∠1=∠2,
∴∠1+∠3=45°,
即∠GAF=∠_________,
又AG=AE,AF=AF,
∴△GAF≌_______,
∴_________=EF,
故DE+BF=EF;
(2)方法迁移:
如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF= ∠DAB,试猜想DE,BF,EF之间有何数量关系,并证明你的猜想;
(3)问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF= ∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF,请直接写出你的猜想(不必说明理由)。
旋转的作图
作旋转图形的步骤
作图基本步骤五步:1.明确三要素;2.找出关键点;3.作出对应点;4.作出新图形;5.写出结论
确定旋转中心
两对对应点连线的垂直平分线的交点
课堂小结
当堂检测
1、完成课本第62页第4题
2、导测
预习安排
1、阅读课本64-66页,完成练习;
2、 完成导学案47页预习导学的内容,组长下节课上课前组织校对答案,经组内讨论不能解决的问题课前把题号或疑问上传本组黑板上。
旋转作图
1、旋转的三要素是什么?
2、旋转的性质是什么?
①对应点到旋转中心的距离相等
②对应点与旋转中心所连线段的夹角等于旋转角
③旋转前、后的图形全等
∵△A′B′C′是由△ABC旋转得到的,
∴OA= OA′、OB=OB′、OC=OC′
∠AOA′=∠BOB′=∠COC′,?ABC≌?A′B′C′
A′
B′
C′
O
A
B
C
几何语言:
旋转中心、旋转方向、旋转角.
温故知新
学习目标
1 、会按要求做出简单平面图形旋转前后的图形,能根据给出的旋转前后的图形,确定旋转中心和旋转角。
2、体会旋转在图形变换中的作用,会利用旋转作图进行计算。
预习导学
组长组织交流预习导学,用红笔标注自己通过预学存在的问题,组长将记录各题完成情况,组织成员讨论出错题目,将未解决问题上传至本组黑板上或准备口头提出。
如无问题则进入反转环节。
例 如图(1),E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
解:∵点A是旋转中心
∴它的对应点是它本身.正方形ABCD中,
AD=AB,∠DAB=90°
∴旋转后点D与点B重合.
设点E的对应点为点E′.
∵旋转后的图形与旋转前的图形全等,
∴∠ABE′=∠ADE =90°,BE′=DE.
因此,在CB的延长线上取点E′,使BE′=
DE,则△ABE′为旋转后的图形(图(2)).
图(1)
图(2)
预习展示
方法2:
F
图中 △ABF 为所求图形.
A
B
C
E
D
方法3:
F
图中 △ABF 为所求图形.
A
B
C
E
D
A
O
将A点绕O沿顺时针方向旋转60?。
作法:
1. 以O为圆心,OA长为半径画圆;
2. 连接OA,用量角器或三角板(限特殊角)作出∠AOB,与圆周交于B点;
3. B点即为所求作。
B
点的旋转作法
画出将线段 AB 绕点 O 按顺时针方向旋转 90°后的图形.
A
B
?
O
A'
B'
作法:
1.将点A绕点O顺时针旋转90?,得点A'
2. 将点B绕点O顺时针旋转90 ?,得点B'
3. 连接A' B', 则线段A' B'即为所求作.
已知△OAB,画出△OAB绕点O逆时针旋转100°后的图形。
B
A
O
A′
B′
1. 作∠AOC=100°,在OC上截取OA′=OA 。
2. 作∠BOD=100°,
在OD上截OB′=OB 。
C
D
注:作旋转后的图形可以转化为作旋转后的对应点。
3. 连接A′B′,则△OA′B′即为所求作。
作法:
归纳总结:旋转作图的步骤
(1)确定旋转 ,旋转 ,旋转 ;
(2)找出图形的关键点;
(3)做出关键点经旋转后的 点;
(4)按图形的顺序依次连接 点,得到旋转后的图形;
(5)写出结论。
中心
角
方向
对应
对应
旋转作图的依据是旋转的 。
性质
12
1.下列图形中,不能由其中一个图形通过旋转而构成的是( )
2.如图所示的图案中,可以由
一个“基本图案”连续旋转45°
得到的图案有 .(填序号)
C
(2)
预习自测
3、等边三角形绕它的中心旋转多少度能与自身重合?正方形呢?正n边形呢?
A/
B/
C/
任意画一个△ABC,以AC中点为中心,把这个三角形旋转180°
预习自测
在Rt△ABC中,∠B=90°,AB=3,,BC=4,请以点A为旋转中心将△ABC逆时针旋转90°。
(1)作出旋转后的图形;
(2)点C的对应点为C ′,求CC ′的长.
B
A
C
C′
B′
互动探究一
利用勾股定理和旋转的性质
变式
如图,△ABC绕点O旋转后,顶点A的对应点为点D,试确定顶点B、C对应点的位置,以及旋转后的三角形.
先将对应点与旋转中心连接,确定旋转方向和旋转角,在此基础上,分别找到各个关键点的对应点所在的射线,然后利用对应点到旋转中心的距离相等来确定对应点的具体位置
已知旋转中心和一对对应点作旋转后的图形的方法:
下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°, 你能画出△OAB 旋转后的图形 △O A ′ B ′ 吗?
A
B
O
A'
B'
互动探究二
网格中旋转90°的画法
归纳:
1.确定关键点与旋转中心所在的矩形.
2.搞清楚是顺时针还是逆时针,旋转矩形,确定对应点.
3.确定旋转后的图形.
如图,在方格纸上建立的平面直角坐标系中,将△ABO绕点O按顺时针方向旋转90°,得到△A1B1O,那么点A1的坐标为( )
变式
(2018?中考)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°
后得到△A2B2C2,请画出△A2B2C2;
变式
A
B
C
D
E
F
ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心.
.
O
确定旋转中心的步骤:
互动探究三
1.连接两组对应点.
2.作对应点连线的垂直平分线.
3.交点就是旋转中心.
变式
在如图所示的4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△ M1N1P1,则其旋转中心是 ,旋转度数是
归纳总结:1、在网格中确定旋转中心,可利
用 ,在所给的点中找到与各对对应点距
离 的点即可。
2、连接两对对应点,分别作出这两条连线的垂直平分线,交点即为旋转中心
如图,△ADE可由△CAB旋转而成,点B的对应点是E,点A的对应点是D,在平面直角坐标系中,三点坐标为A(1,0)、B(3,0)、C(1,4).
请找出旋转中心P的位置,并写出P的坐标和旋转角度
A
B
O
C
D
E
x
y
P(3,2)
变式
如图,点E是正方形ABCD内一点,连接AE、BE、CE,,若AE=1,BE=2,CE=3,则求∠BEA的度数.
解析:将△ABE绕点B顺时针旋转90°到△CBE′的位置,连接EE′,
由旋转性质知BE=BE′=2,∠EBE′=90°,
∴∠BE'E=45°,则根据勾股定理,得
在△EE′C中,E′C=1,EC=3,
EE′=????????
?
EE′=????????
?
由勾股定理逆定理可知∠EE′C=90°,
∴∠BE′C=∠BE′E+∠EE′C=135°.
互动探究四
能力提升
探究问题:
(1)方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF。
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上,
∵∠EAF=45°,
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°,
∵∠1=∠2,
∴∠1+∠3=45°,
即∠GAF=∠_________,
又AG=AE,AF=AF,
∴△GAF≌_______,
∴_________=EF,
故DE+BF=EF;
(2)方法迁移:
如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF= ∠DAB,试猜想DE,BF,EF之间有何数量关系,并证明你的猜想;
(3)问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF= ∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF,请直接写出你的猜想(不必说明理由)。
旋转的作图
作旋转图形的步骤
作图基本步骤五步:1.明确三要素;2.找出关键点;3.作出对应点;4.作出新图形;5.写出结论
确定旋转中心
两对对应点连线的垂直平分线的交点
课堂小结
当堂检测
1、完成课本第62页第4题
2、导测
预习安排
1、阅读课本64-66页,完成练习;
2、 完成导学案47页预习导学的内容,组长下节课上课前组织校对答案,经组内讨论不能解决的问题课前把题号或疑问上传本组黑板上。
同课章节目录
