23.2.1中心对称-人教版九年级数学上册课件(19张)
文档属性
| 名称 | 23.2.1中心对称-人教版九年级数学上册课件(19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 14:01:04 | ||
图片预览




文档简介
23.2.1 中心对称
学习目标
1. 能说出中心对称、对称中心、关于对称中心的对称点等概念。
2.会利用中心对称的性质作出 与某一图形成中心对称的图形,会确定对称中心的位置。
A
B
D
C
O
A
B
D
C
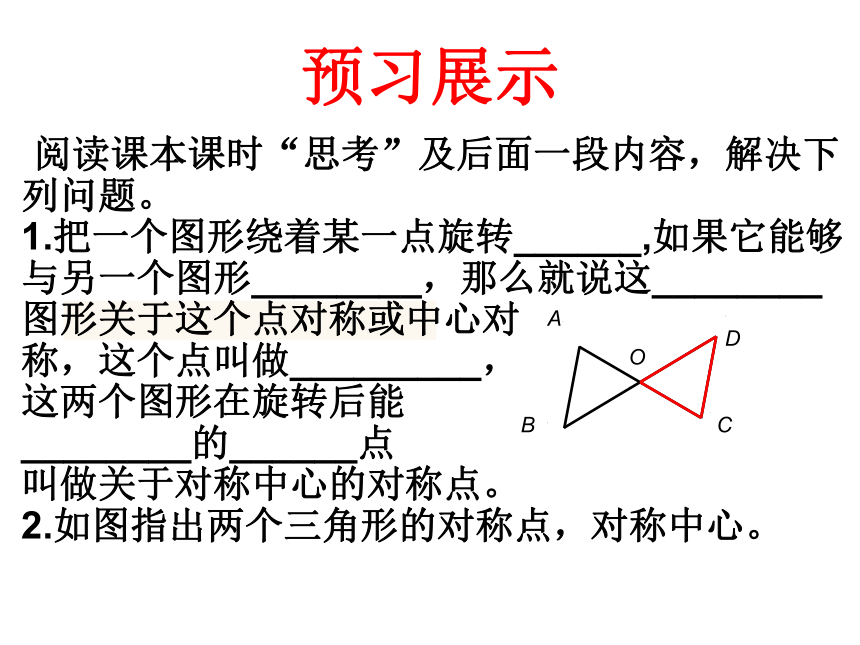
预习展示
阅读课本课时“思考”及后面一段内容,解决下列问题。
1.把一个图形绕着某一点旋转______,如果它能够与另一个图形________,那么就说这________图形关于这个点对称或中心对
称,这个点叫做_________,
这两个图形在旋转后能
________的______点
叫做关于对称中心的对称点。
2.如图指出两个三角形的对称点,对称中心。
O
阅读课本课时“思考”后面第二段开始至本课时结束,解决导学案P47页中间问题,总结中心对称的性质:
中心对称的______图形,
对称点所连线段都经过
______,而且被_______
平分。中心对称的两个图形是______图形。
预习展示
轴对称 与中心对称定义、性质对比图
轴对称
中心对称
定
义
1
2
3
有一条对称轴—直线
图形沿轴对折,(翻转达180度。)
翻转后与另一个图形重合。
有一个对称中心—点。
图形绕中心旋转180度。
旋转后与另一个图形重合。
性
质
1
2
两个图形是全等形。
对称轴是对称点连线的垂直平分线。
两个图形是全等形。
对称点连线都过对称中心,
且被对称中心平分
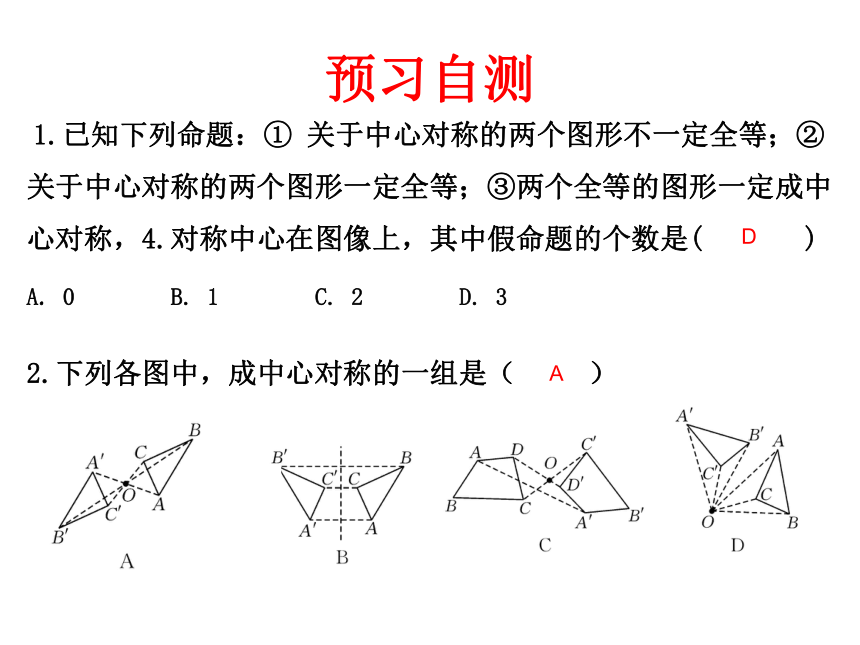
预习自测
1.已知下列命题:① 关于中心对称的两个图形不一定全等;②关于中心对称的两个图形一定全等;③两个全等的图形一定成中心对称,4.对称中心在图像上,其中假命题的个数是( )
A. 0 B. 1 C. 2 D. 3
.
D
2.下列各图中,成中心对称的一组是( )
A
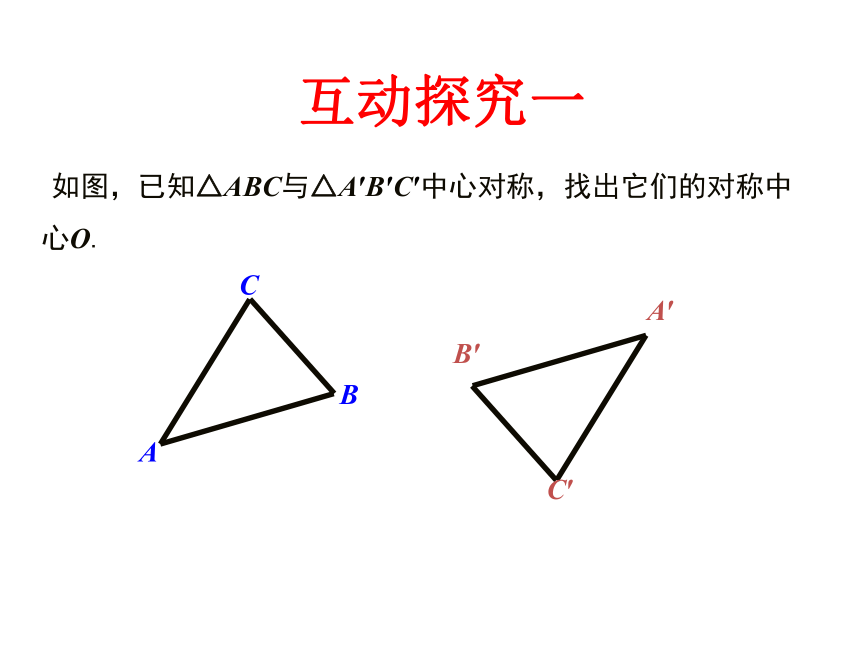
如图,已知△ABC与△A′B′C′中心对称,找出它们的对称中心O.
A
B
C
A′
B′
C′
互动探究一
解法1:根据观察,B、B′应是对应点,连结BB′,用刻度尺找出BB′的中点O,则点O即为所求(如图).
A
B
C
A′
B′
C′
O
O
解法2:根据观察,B、B′及C、C′应是两组对应点,连结BB′、CC′,BB′、CC′相交于点O,则点O即为所求(如图).
A
B
C
A′
B′
C′
注意:如果限制只用直尺作图,我们用解法2.
新课讲解
合作探究二
变式演练:如图,将一张直角三角形纸片ABC沿中位线D E剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E 到了点E′位置,则四边形ACE′E 的形状是 ( )(说明理由)
追问:(1)若DE=2;求EE,的长
(2)四边形BEB, E,形状?说明理由
如图,已知△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中CD边上的高是( )
A.2 B.4
C.6 D.8
A
B
C
D
O
如图23.2-5,选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.
解:
A′
C′
B′
△A′B′C′即为所求的三角形。
合作探究三
[归纳总结] 作中心对称的图形的一般步骤是
①确定代表性的点(线段的端点)
②作出每个代表性的点的对称点;
③按照原图形的形状顺次连接各对称点.
A
B
C
D
O
∴四边形A`B`C`D是
所求的四边形。
A`
.
D`
.
C`
.
B`
.
若点O是BC的中点呢?
合作探究四
追问:求B1B2
(2,-1)
能力提升
当堂检测
如图,已知等边△ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称.
O
A
B
C
(7,-2)
课堂小结
把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就是对称中心.
(1)中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分.
(2)中心对称的两个图形是全等图形.
当堂检测
在规定的时间内,完成导学测评第1-9(必做)和10(选做)题,组长收齐后校对答案,将完成情况给老师汇报。
预习安排
1.阅读课本66-67页,完成练习。
2.完成导学案49页预习导学的内容,组长下节课上课前组织校对答案,经组内讨论不能解决的问题课前把题号或疑问上传本组黑板上。
谢谢大家
学习目标
1. 能说出中心对称、对称中心、关于对称中心的对称点等概念。
2.会利用中心对称的性质作出 与某一图形成中心对称的图形,会确定对称中心的位置。
A
B
D
C
O
A
B
D
C
预习展示
阅读课本课时“思考”及后面一段内容,解决下列问题。
1.把一个图形绕着某一点旋转______,如果它能够与另一个图形________,那么就说这________图形关于这个点对称或中心对
称,这个点叫做_________,
这两个图形在旋转后能
________的______点
叫做关于对称中心的对称点。
2.如图指出两个三角形的对称点,对称中心。
O
阅读课本课时“思考”后面第二段开始至本课时结束,解决导学案P47页中间问题,总结中心对称的性质:
中心对称的______图形,
对称点所连线段都经过
______,而且被_______
平分。中心对称的两个图形是______图形。
预习展示
轴对称 与中心对称定义、性质对比图
轴对称
中心对称
定
义
1
2
3
有一条对称轴—直线
图形沿轴对折,(翻转达180度。)
翻转后与另一个图形重合。
有一个对称中心—点。
图形绕中心旋转180度。
旋转后与另一个图形重合。
性
质
1
2
两个图形是全等形。
对称轴是对称点连线的垂直平分线。
两个图形是全等形。
对称点连线都过对称中心,
且被对称中心平分
预习自测
1.已知下列命题:① 关于中心对称的两个图形不一定全等;②关于中心对称的两个图形一定全等;③两个全等的图形一定成中心对称,4.对称中心在图像上,其中假命题的个数是( )
A. 0 B. 1 C. 2 D. 3
.
D
2.下列各图中,成中心对称的一组是( )
A
如图,已知△ABC与△A′B′C′中心对称,找出它们的对称中心O.
A
B
C
A′
B′
C′
互动探究一
解法1:根据观察,B、B′应是对应点,连结BB′,用刻度尺找出BB′的中点O,则点O即为所求(如图).
A
B
C
A′
B′
C′
O
O
解法2:根据观察,B、B′及C、C′应是两组对应点,连结BB′、CC′,BB′、CC′相交于点O,则点O即为所求(如图).
A
B
C
A′
B′
C′
注意:如果限制只用直尺作图,我们用解法2.
新课讲解
合作探究二
变式演练:如图,将一张直角三角形纸片ABC沿中位线D E剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E 到了点E′位置,则四边形ACE′E 的形状是 ( )(说明理由)
追问:(1)若DE=2;求EE,的长
(2)四边形BEB, E,形状?说明理由
如图,已知△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中CD边上的高是( )
A.2 B.4
C.6 D.8
A
B
C
D
O
如图23.2-5,选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.
解:
A′
C′
B′
△A′B′C′即为所求的三角形。
合作探究三
[归纳总结] 作中心对称的图形的一般步骤是
①确定代表性的点(线段的端点)
②作出每个代表性的点的对称点;
③按照原图形的形状顺次连接各对称点.
A
B
C
D
O
∴四边形A`B`C`D是
所求的四边形。
A`
.
D`
.
C`
.
B`
.
若点O是BC的中点呢?
合作探究四
追问:求B1B2
(2,-1)
能力提升
当堂检测
如图,已知等边△ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称.
O
A
B
C
(7,-2)
课堂小结
把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就是对称中心.
(1)中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分.
(2)中心对称的两个图形是全等图形.
当堂检测
在规定的时间内,完成导学测评第1-9(必做)和10(选做)题,组长收齐后校对答案,将完成情况给老师汇报。
预习安排
1.阅读课本66-67页,完成练习。
2.完成导学案49页预习导学的内容,组长下节课上课前组织校对答案,经组内讨论不能解决的问题课前把题号或疑问上传本组黑板上。
谢谢大家
同课章节目录
