23.3相似三角形(1)平行线判定三角形相似-华东师大版九年级数学上册课件(15张)
文档属性
| 名称 | 23.3相似三角形(1)平行线判定三角形相似-华东师大版九年级数学上册课件(15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 00:00:00 | ||
图片预览


文档简介
§23.3 相似三角形(1)
——平行线判定相似
1、两个边数相同的多边形,如果各边对应_________,
各角对应_______,那么这两个多边形相似。
2、相似多边形的______________成比例,
________相等。
成比例
相等
对应边
对应角
知识回顾
知识点
1
相似三角形的概念
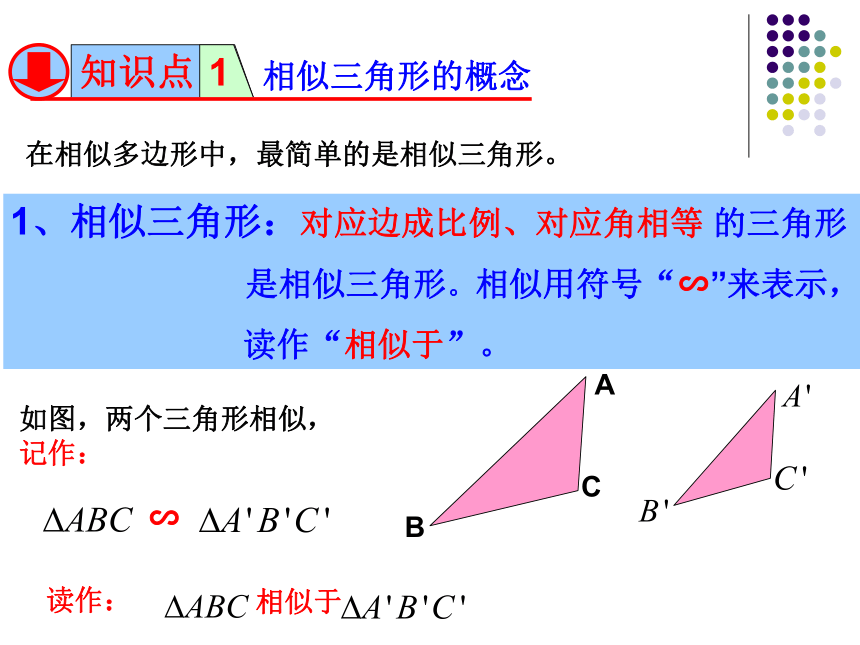
在相似多边形中,最简单的是相似三角形。
1、相似三角形:对应边成比例、对应角相等 的三角形
是相似三角形。相似用符号“∽”来表示,
读作“相似于”。
C
A
B
如图,两个三角形相似,记作:
∽
读作:
相似于
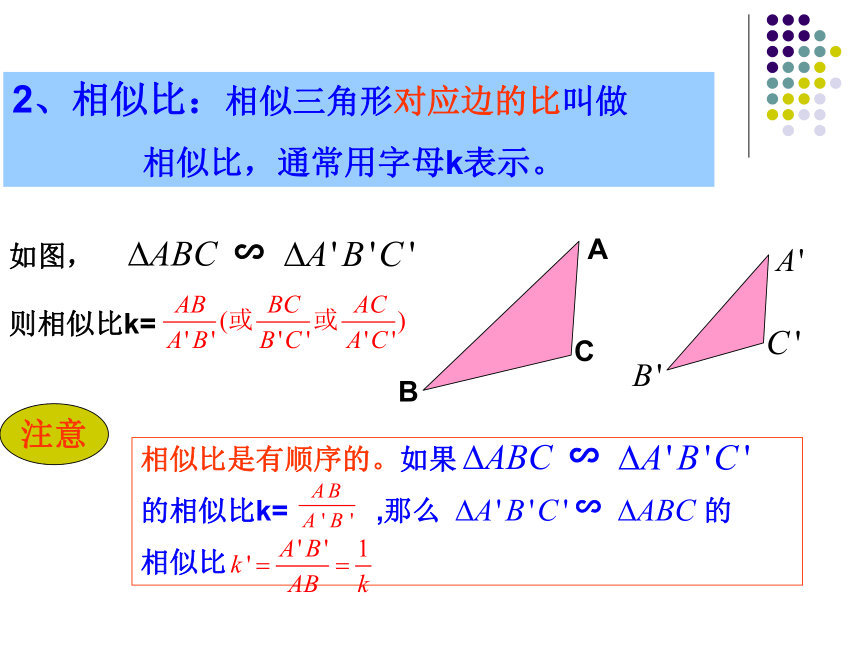
2、相似比:相似三角形对应边的比叫做
相似比,通常用字母k表示。
C
A
B
如图,
∽
则相似比k=
注意
相似比是有顺序的。如果
的相似比k= ,那么 的
相似比
∽
∽
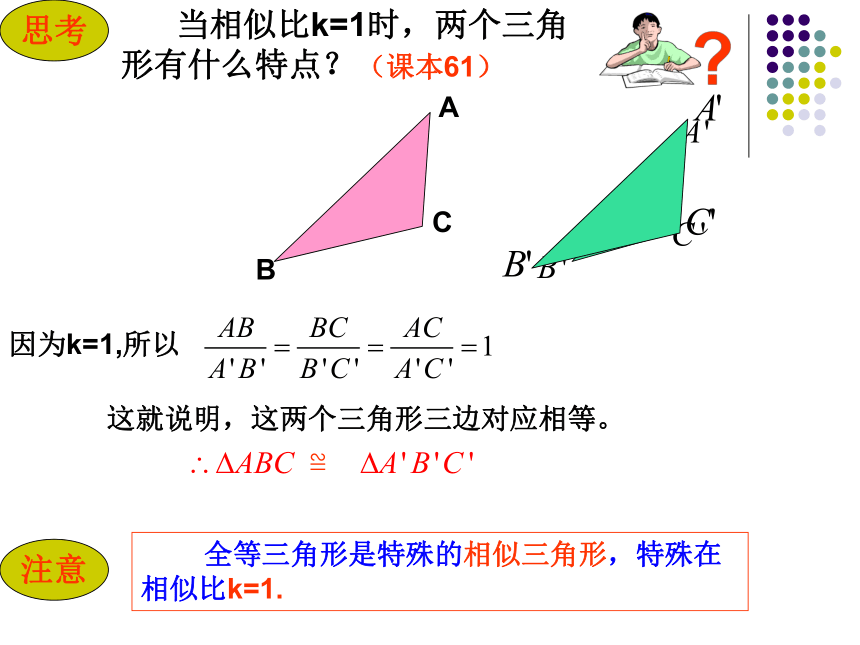
思考
当相似比k=1时,两个三角形有什么特点?
C
A
B
因为k=1,所以
这就说明,这两个三角形三边对应相等。
≌
注意
全等三角形是特殊的相似三角形,特殊在相似比k=1.
(课本61)
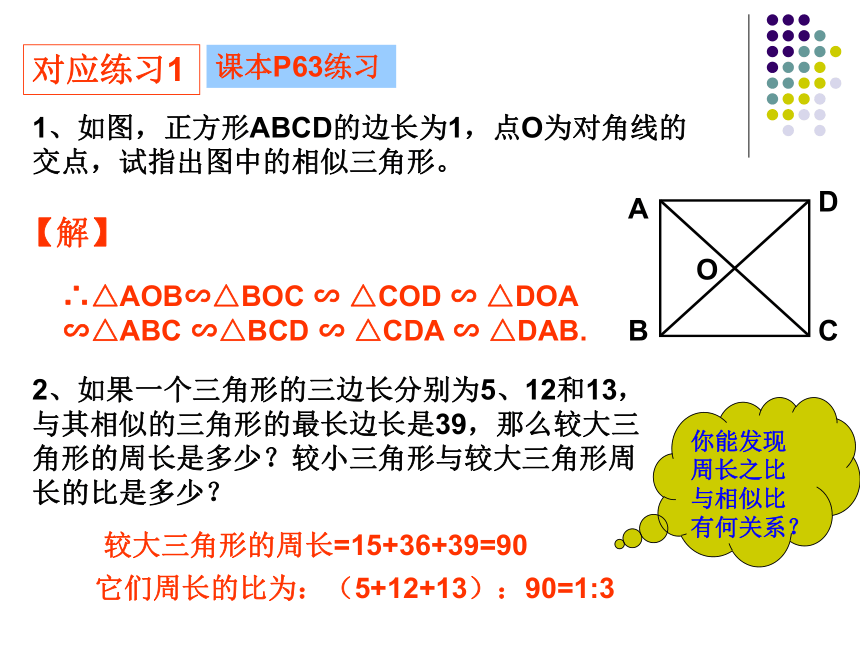
对应练习1
课本P63练习
1、如图,正方形ABCD的边长为1,点O为对角线的交点,试指出图中的相似三角形。
O
A
B
C
D
【解】
∴△AOB∽△BOC ∽ △COD ∽ △DOA
∽△ABC ∽△BCD ∽ △CDA ∽ △DAB.
2、如果一个三角形的三边长分别为5、12和13,与其相似的三角形的最长边长是39,那么较大三角形的周长是多少?较小三角形与较大三角形周长的比是多少?
你能发现周长之比与相似比有何关系?
较大三角形的周长=15+36+39=90
它们周长的比为:(5+12+13):90=1:3
知识点
2
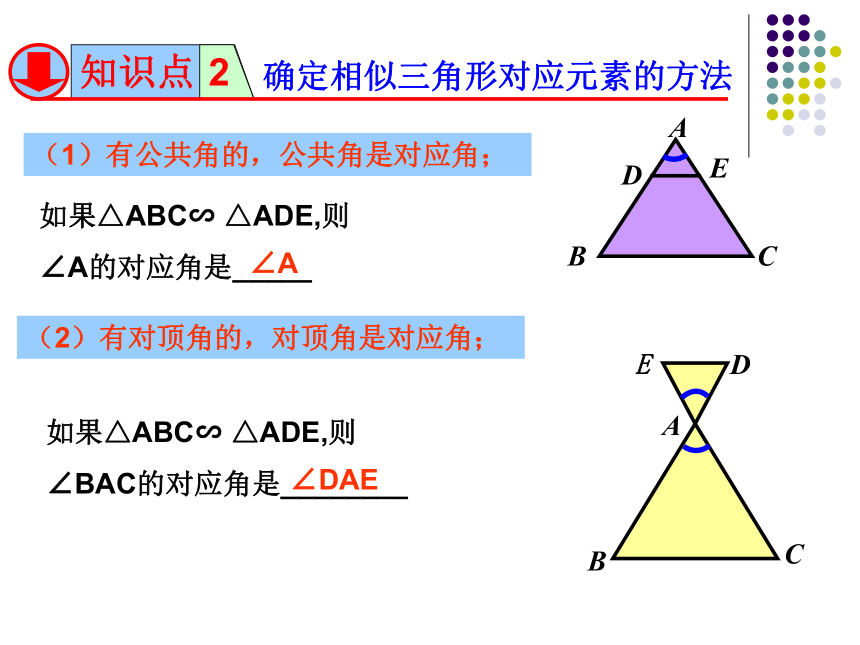
确定相似三角形对应元素的方法
(1)有公共角的,公共角是对应角;
A
B
C
D
E
如果△ABC∽ △ADE,则
∠A的对应角是_____
∠A
(2)有对顶角的,对顶角是对应角;
A
B
C
E
D
如果△ABC∽ △ADE,则
∠BAC的对应角是________
∠DAE
C
A
B
D
E
F
(△ABC∽△DFE)
(3)对应角所对的边是对应边,对应角所夹的边是对应边;
如果∠A= ∠D,则BC
EF
∠A= ∠D
∠B= ∠F
如果
则AB
DF
(4)对应边所对的角是对应角,对应边所夹的角是对应角;
C
A
B
D
E
F
(△ABC∽△DFE)
如果AB对应DF,则∠C=______;
∠E
如果AB对应DF,
BC对应EF
则∠B=____.
∠F
知识探索
问题1
如图,DE∥BC, △ADE与△ABC是否相似?
要说明△ADE∽△ABC,根据定义,就要证明①对应角相等;②对应边成比例。
①在△ADE与△ABC中, ∠A=∠A,
∵DE//BC,
∴∠ADE=∠B, ∠AED=∠C.
F
②过点D作DF∥AC交BC于F点。
∵DE∥BC,
∴DECF是平行四边形,
∴CF=DE
∵DE∥BC,
又∵DF∥AC
而CF=DE
又∵
∴△ADE∽△ABC
而∠A=∠A,∠ADE=∠B, ∠AED=∠C.
A
B
C
E
D
问题2
如图,DE∥BC, △ADE与△ABC是否相似?
∴△ADE∽△ABC
将△ADE绕A点旋转 得到
如图,则△ADE与 ______.
全等
由问题1知:
△ABC
∽
(课本P63思考)
知识概括
平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似.
A
B
C
D
E
“A”字形
∵DE∥BC, ∴△ADE∽ △ABC
A
B
C
D
E
“X”字形
∵DE∥BC, ∴△ADE∽ △ABC
知识点
3
利用平行线判定三角形相似
例1
例题解析
如图,在△ABC中,点D是边AB三等分点,DE∥BC,DE=5,求BC的长。
B
A
C
D
E
分析:
点D是边AB三等分点
DE∥BC
【解】
∵DE∥BC
∴△ADE∽ △ABC(
)
平行于三角形一边的直线,
和其他两边相交所构成的三角形和原三角形相似
∵点D是边AB三等分点
∴BC=3DE=15
对应练习1
课本P64练习
如图,在△ABC中,点D是边AB四等分
点,DE∥AC,DF ∥ BC,AC=8,BC=12.
求四边形DECF的周长。
F
A
B
C
D
E
课堂小结
1、相似三角形的性质:
对应边成比例,对应角相等。
2、相似三角形的相似比:
对应边的比叫做相似比,它有顺序之分。
3、对应边和对应角的找法怎样?
4、相似三角形判定的预备定理:
A
B
C
D
E
“A”字形
A
B
C
D
E
“X”字形
——平行线判定相似
1、两个边数相同的多边形,如果各边对应_________,
各角对应_______,那么这两个多边形相似。
2、相似多边形的______________成比例,
________相等。
成比例
相等
对应边
对应角
知识回顾
知识点
1
相似三角形的概念
在相似多边形中,最简单的是相似三角形。
1、相似三角形:对应边成比例、对应角相等 的三角形
是相似三角形。相似用符号“∽”来表示,
读作“相似于”。
C
A
B
如图,两个三角形相似,记作:
∽
读作:
相似于
2、相似比:相似三角形对应边的比叫做
相似比,通常用字母k表示。
C
A
B
如图,
∽
则相似比k=
注意
相似比是有顺序的。如果
的相似比k= ,那么 的
相似比
∽
∽
思考
当相似比k=1时,两个三角形有什么特点?
C
A
B
因为k=1,所以
这就说明,这两个三角形三边对应相等。
≌
注意
全等三角形是特殊的相似三角形,特殊在相似比k=1.
(课本61)
对应练习1
课本P63练习
1、如图,正方形ABCD的边长为1,点O为对角线的交点,试指出图中的相似三角形。
O
A
B
C
D
【解】
∴△AOB∽△BOC ∽ △COD ∽ △DOA
∽△ABC ∽△BCD ∽ △CDA ∽ △DAB.
2、如果一个三角形的三边长分别为5、12和13,与其相似的三角形的最长边长是39,那么较大三角形的周长是多少?较小三角形与较大三角形周长的比是多少?
你能发现周长之比与相似比有何关系?
较大三角形的周长=15+36+39=90
它们周长的比为:(5+12+13):90=1:3
知识点
2
确定相似三角形对应元素的方法
(1)有公共角的,公共角是对应角;
A
B
C
D
E
如果△ABC∽ △ADE,则
∠A的对应角是_____
∠A
(2)有对顶角的,对顶角是对应角;
A
B
C
E
D
如果△ABC∽ △ADE,则
∠BAC的对应角是________
∠DAE
C
A
B
D
E
F
(△ABC∽△DFE)
(3)对应角所对的边是对应边,对应角所夹的边是对应边;
如果∠A= ∠D,则BC
EF
∠A= ∠D
∠B= ∠F
如果
则AB
DF
(4)对应边所对的角是对应角,对应边所夹的角是对应角;
C
A
B
D
E
F
(△ABC∽△DFE)
如果AB对应DF,则∠C=______;
∠E
如果AB对应DF,
BC对应EF
则∠B=____.
∠F
知识探索
问题1
如图,DE∥BC, △ADE与△ABC是否相似?
要说明△ADE∽△ABC,根据定义,就要证明①对应角相等;②对应边成比例。
①在△ADE与△ABC中, ∠A=∠A,
∵DE//BC,
∴∠ADE=∠B, ∠AED=∠C.
F
②过点D作DF∥AC交BC于F点。
∵DE∥BC,
∴DECF是平行四边形,
∴CF=DE
∵DE∥BC,
又∵DF∥AC
而CF=DE
又∵
∴△ADE∽△ABC
而∠A=∠A,∠ADE=∠B, ∠AED=∠C.
A
B
C
E
D
问题2
如图,DE∥BC, △ADE与△ABC是否相似?
∴△ADE∽△ABC
将△ADE绕A点旋转 得到
如图,则△ADE与 ______.
全等
由问题1知:
△ABC
∽
(课本P63思考)
知识概括
平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似.
A
B
C
D
E
“A”字形
∵DE∥BC, ∴△ADE∽ △ABC
A
B
C
D
E
“X”字形
∵DE∥BC, ∴△ADE∽ △ABC
知识点
3
利用平行线判定三角形相似
例1
例题解析
如图,在△ABC中,点D是边AB三等分点,DE∥BC,DE=5,求BC的长。
B
A
C
D
E
分析:
点D是边AB三等分点
DE∥BC
【解】
∵DE∥BC
∴△ADE∽ △ABC(
)
平行于三角形一边的直线,
和其他两边相交所构成的三角形和原三角形相似
∵点D是边AB三等分点
∴BC=3DE=15
对应练习1
课本P64练习
如图,在△ABC中,点D是边AB四等分
点,DE∥AC,DF ∥ BC,AC=8,BC=12.
求四边形DECF的周长。
F
A
B
C
D
E
课堂小结
1、相似三角形的性质:
对应边成比例,对应角相等。
2、相似三角形的相似比:
对应边的比叫做相似比,它有顺序之分。
3、对应边和对应角的找法怎样?
4、相似三角形判定的预备定理:
A
B
C
D
E
“A”字形
A
B
C
D
E
“X”字形
