23.3相似三角形(2)判定1-华东师大版九年级数学上册课件(15张)
文档属性
| 名称 | 23.3相似三角形(2)判定1-华东师大版九年级数学上册课件(15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览


文档简介
§23.3 相似三角形(2)
——判定1
知识回顾
相似三角形的判定方法:
①定义:三边对应成比例,三个角对应相等的两个三角形相似。
②平行线判定:平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形和原三角形相似。
知识探索
问题1
我们知道,根据相似三角形的定义,要判定两个三角形是否相似,必须判断它们的对应边是否成比例,对应角是否相等。那么是否存在简便的方法?
问题2
我们知道,判定两个三角形全等的方法有:
________________________________________
__________________________________.
⑴两边及夹角(SAS);
⑵两角及夹边(ASA);
⑶两角及对边(AAS);
⑷三边(SSS)
相似三角形是否有类似的判定方法?
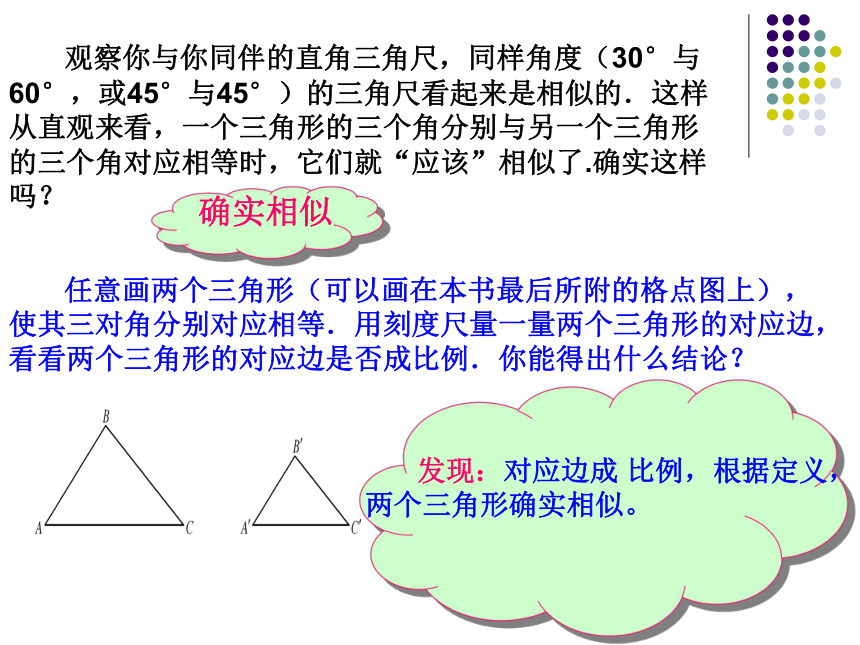
观察你与你同伴的直角三角尺,同样角度(30°与60°,或45°与45°)的三角尺看起来是相似的.这样从直观来看,一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就“应该”相似了.确实这样吗?
任意画两个三角形(可以画在本书最后所附的格点图上),使其三对角分别对应相等.用刻度尺量一量两个三角形的对应边,看看两个三角形的对应边是否成比例.你能得出什么结论?
发现:对应边成 比例,根据定义,两个三角形确实相似。
确实相似
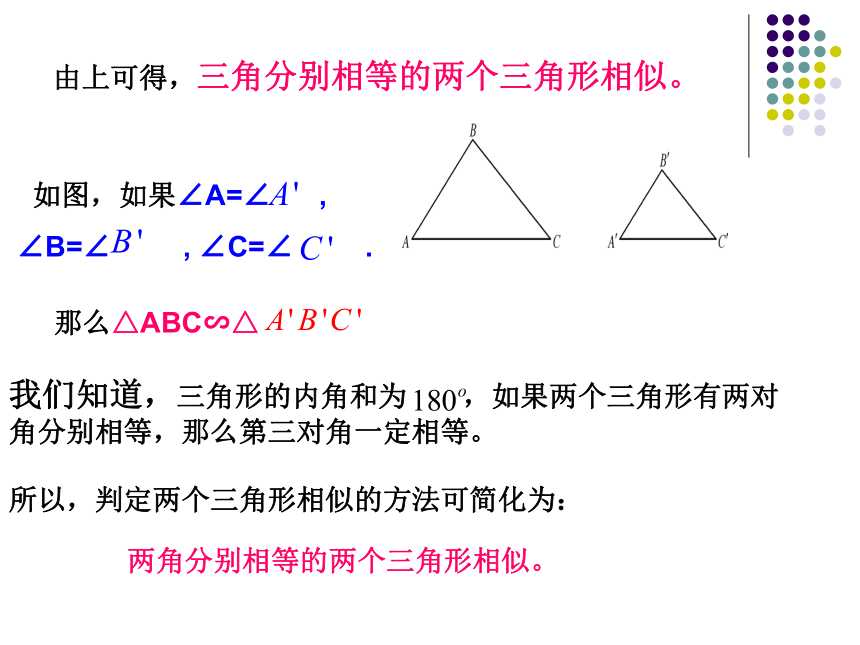
由上可得,三角分别相等的两个三角形相似。
如图,如果∠A=∠ ,
∠B=∠ , ∠C=∠ .
那么△ABC∽△
我们知道,三角形的内角和为 ,如果两个三角形有两对角分别相等,那么第三对角一定相等。
所以,判定两个三角形相似的方法可简化为:
两角分别相等的两个三角形相似。
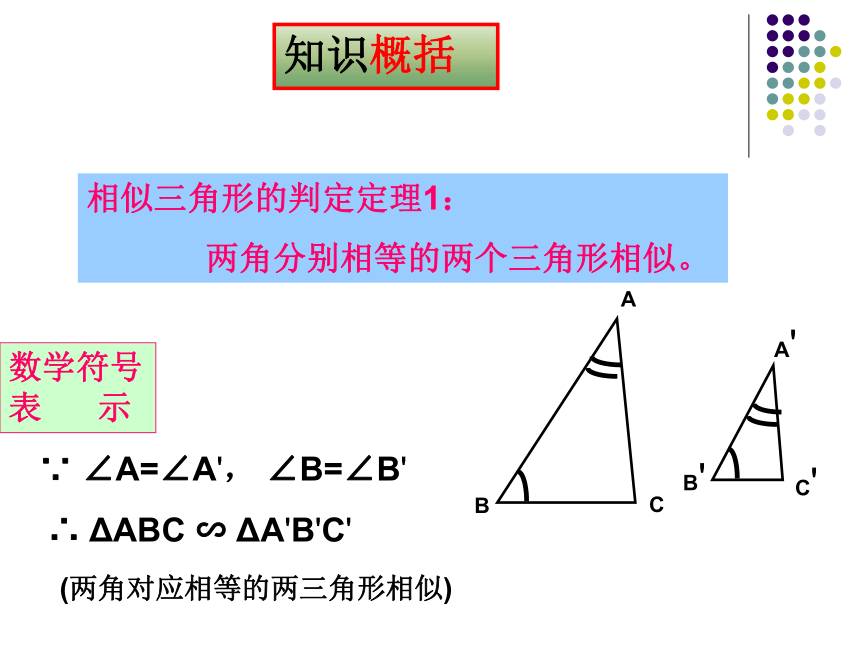
知识概括
相似三角形的判定定理1:
两角分别相等的两个三角形相似。
数学符号表 示
C
A
A'
B
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
(两角对应相等的两三角形相似)
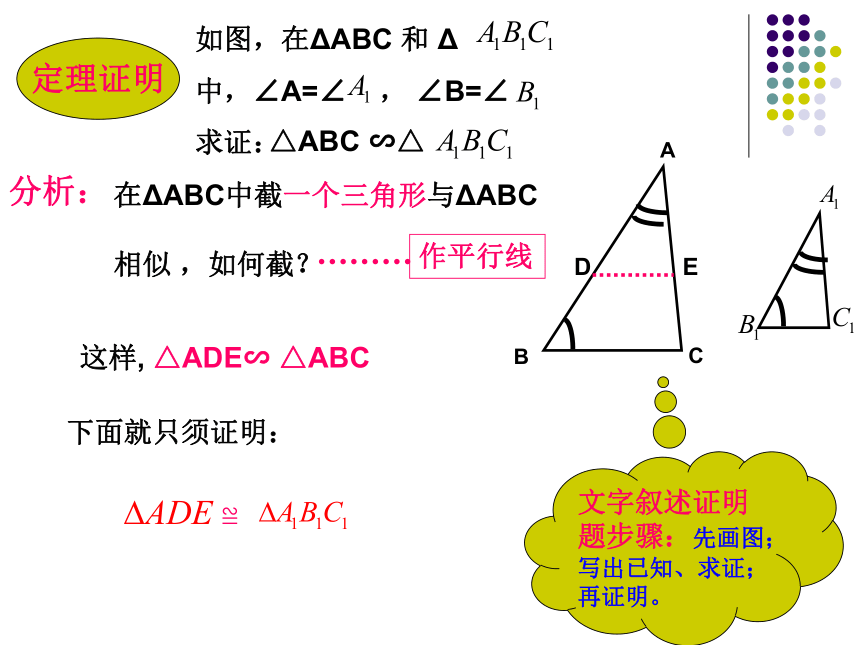
定理证明
如图,在ΔABC 和 Δ
中,∠A=∠ , ∠B=∠
求证:
△ABC ∽△
文字叙述证明题步骤:先画图;写出已知、求证;再证明。
C
A
B
分析:
在ΔABC中截一个三角形与ΔABC
相似 ,如何截?
作平行线
D
E
这样, △ADE∽ △ABC
下面就只须证明:
≌
C
A
B
【证明】
D
E
在AB上截取AD= ,过D点作
DE∥BC交AC于点E,则
△ADE∽ △ABC
∵DE∥BC
∴∠ADE=∠B
又∠B=∠
∴∠ADE=∠
在△ADE和△ 中,
∵∠A=∠ , AD= , ∠ADE=∠ .
∴△ADE≌△
∴△ABC ∽△
例题解析
如图,△ABC中,DE∥BC,EF∥AB,
求证: △ADE∽△EFC.
例1
分析:
DE∥BC
∠ =∠
AED
C
EF∥AB
∠ =∠
A
CEF
【证明】
∵DE∥BC
∴∠AED=∠C
又∵EF∥AB
∴∠A=∠CEF
∴△ADE∽△EFC( )
两角分别相等的两个三角形相似
思考:还有其他方法没有?
想一想
课本66页
在上例中,如果点D恰好是边AB的中点,那么
①点E是边AC的中点吗?
②DE和BC有什么关系?
③△ADE与 △CEF又有什么特殊关系?
①点E是边AC的中点。
结论:过三角形一边中点作另一边的平行线一定平分第三边。
②DE是BC的一半。
③△ADE≌△CEF
课堂练习
1、(课本67页)如图DG∥EH∥FI∥BC,找出图中所有的相似三角形.
【解】
△ADG∽△AEH ∽△AFI ∽△ABC
2. (课本67页)找出图中所有的相似三角形,
并说明理由。
【解】
△ACD∽△BCD ∽△ABC
理由:
两角分别相等的两个三角形相似
(1)、两个等边三角形相似 ( )
(2)、两个直角三角形相似 ( )
(3)、两个等腰直角三角形都相似( )
(4)、有一个角为50°的两个等腰三角形相似( )
(5)、有一个角为100°的两个等腰三角形相似( )
3、判断下列说法是否正确:
4.如图,在△ABC和△CDE中,∠B=∠D=90°,C为线段BD上一点,且AC⊥CE,
证明:△ABC∽△CDE.
5.如图,在△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=∠3.
求证:△BCD∽△CDE.
7.如图,AE与BD交于点C,∠DME=∠A=∠B,且DM交AC于F,ME交BC于G,
求证:△AMF∽△BGM.
6.如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE=∠C,求证:△ABF∽△EAD.
课堂作业
P75 1、2、4(1)
——判定1
知识回顾
相似三角形的判定方法:
①定义:三边对应成比例,三个角对应相等的两个三角形相似。
②平行线判定:平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形和原三角形相似。
知识探索
问题1
我们知道,根据相似三角形的定义,要判定两个三角形是否相似,必须判断它们的对应边是否成比例,对应角是否相等。那么是否存在简便的方法?
问题2
我们知道,判定两个三角形全等的方法有:
________________________________________
__________________________________.
⑴两边及夹角(SAS);
⑵两角及夹边(ASA);
⑶两角及对边(AAS);
⑷三边(SSS)
相似三角形是否有类似的判定方法?
观察你与你同伴的直角三角尺,同样角度(30°与60°,或45°与45°)的三角尺看起来是相似的.这样从直观来看,一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就“应该”相似了.确实这样吗?
任意画两个三角形(可以画在本书最后所附的格点图上),使其三对角分别对应相等.用刻度尺量一量两个三角形的对应边,看看两个三角形的对应边是否成比例.你能得出什么结论?
发现:对应边成 比例,根据定义,两个三角形确实相似。
确实相似
由上可得,三角分别相等的两个三角形相似。
如图,如果∠A=∠ ,
∠B=∠ , ∠C=∠ .
那么△ABC∽△
我们知道,三角形的内角和为 ,如果两个三角形有两对角分别相等,那么第三对角一定相等。
所以,判定两个三角形相似的方法可简化为:
两角分别相等的两个三角形相似。
知识概括
相似三角形的判定定理1:
两角分别相等的两个三角形相似。
数学符号表 示
C
A
A'
B
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
(两角对应相等的两三角形相似)
定理证明
如图,在ΔABC 和 Δ
中,∠A=∠ , ∠B=∠
求证:
△ABC ∽△
文字叙述证明题步骤:先画图;写出已知、求证;再证明。
C
A
B
分析:
在ΔABC中截一个三角形与ΔABC
相似 ,如何截?
作平行线
D
E
这样, △ADE∽ △ABC
下面就只须证明:
≌
C
A
B
【证明】
D
E
在AB上截取AD= ,过D点作
DE∥BC交AC于点E,则
△ADE∽ △ABC
∵DE∥BC
∴∠ADE=∠B
又∠B=∠
∴∠ADE=∠
在△ADE和△ 中,
∵∠A=∠ , AD= , ∠ADE=∠ .
∴△ADE≌△
∴△ABC ∽△
例题解析
如图,△ABC中,DE∥BC,EF∥AB,
求证: △ADE∽△EFC.
例1
分析:
DE∥BC
∠ =∠
AED
C
EF∥AB
∠ =∠
A
CEF
【证明】
∵DE∥BC
∴∠AED=∠C
又∵EF∥AB
∴∠A=∠CEF
∴△ADE∽△EFC( )
两角分别相等的两个三角形相似
思考:还有其他方法没有?
想一想
课本66页
在上例中,如果点D恰好是边AB的中点,那么
①点E是边AC的中点吗?
②DE和BC有什么关系?
③△ADE与 △CEF又有什么特殊关系?
①点E是边AC的中点。
结论:过三角形一边中点作另一边的平行线一定平分第三边。
②DE是BC的一半。
③△ADE≌△CEF
课堂练习
1、(课本67页)如图DG∥EH∥FI∥BC,找出图中所有的相似三角形.
【解】
△ADG∽△AEH ∽△AFI ∽△ABC
2. (课本67页)找出图中所有的相似三角形,
并说明理由。
【解】
△ACD∽△BCD ∽△ABC
理由:
两角分别相等的两个三角形相似
(1)、两个等边三角形相似 ( )
(2)、两个直角三角形相似 ( )
(3)、两个等腰直角三角形都相似( )
(4)、有一个角为50°的两个等腰三角形相似( )
(5)、有一个角为100°的两个等腰三角形相似( )
3、判断下列说法是否正确:
4.如图,在△ABC和△CDE中,∠B=∠D=90°,C为线段BD上一点,且AC⊥CE,
证明:△ABC∽△CDE.
5.如图,在△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=∠3.
求证:△BCD∽△CDE.
7.如图,AE与BD交于点C,∠DME=∠A=∠B,且DM交AC于F,ME交BC于G,
求证:△AMF∽△BGM.
6.如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE=∠C,求证:△ABF∽△EAD.
课堂作业
P75 1、2、4(1)
