23.3相似三角形(3)判定2-华东师大版九年级数学上册课件(20张)
文档属性
| 名称 | 23.3相似三角形(3)判定2-华东师大版九年级数学上册课件(20张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 11:12:02 | ||
图片预览




文档简介
§23.3 相似三角形(3)
——判定2
知识回顾
三角形相似的判定方法:
平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似.
①平行线判定三角形相似:
②三角形相似的判定定理1:
两角分别相等的两个三角形相似。
知识探索
观察下图,如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE与△ABC相似呢?
图中两个三角形的一组对应边
AD与AB的长度的比值为_____.
将点E由点A开始在AC上移
动,可以发现当AE=
________AC时,△ADE与△ABC似乎相似.
此时,
E
猜想: 如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。
猜想证明
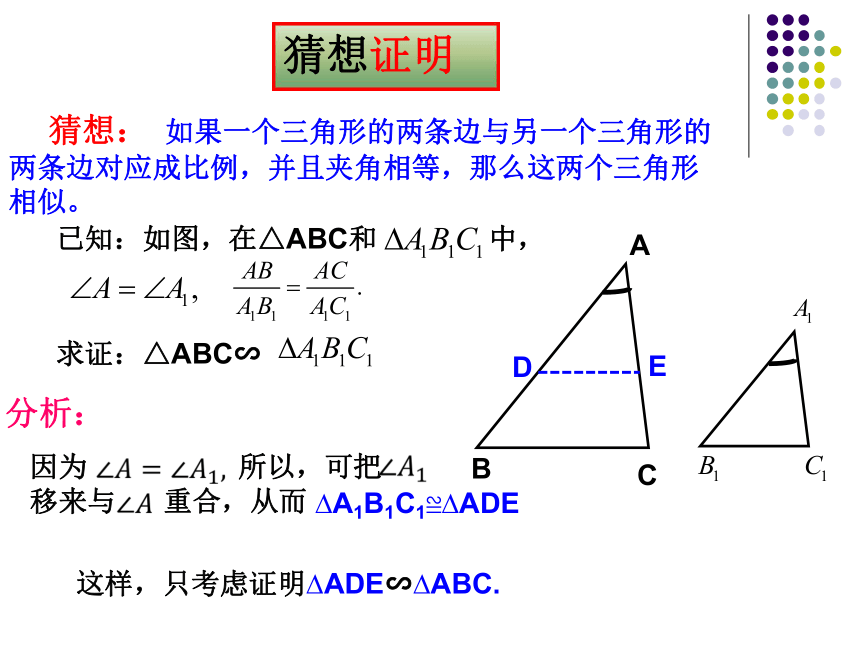
猜想: 如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。
已知:如图,在△ABC和 中,
求证:△ABC∽
C
A
B
分析:
D
E
这样,只考虑证明?ADE∽?ABC.
因为 所以,可把
移来与 重合,从而
?A1B1C1≌?ADE
C
A
B
证明
D
E
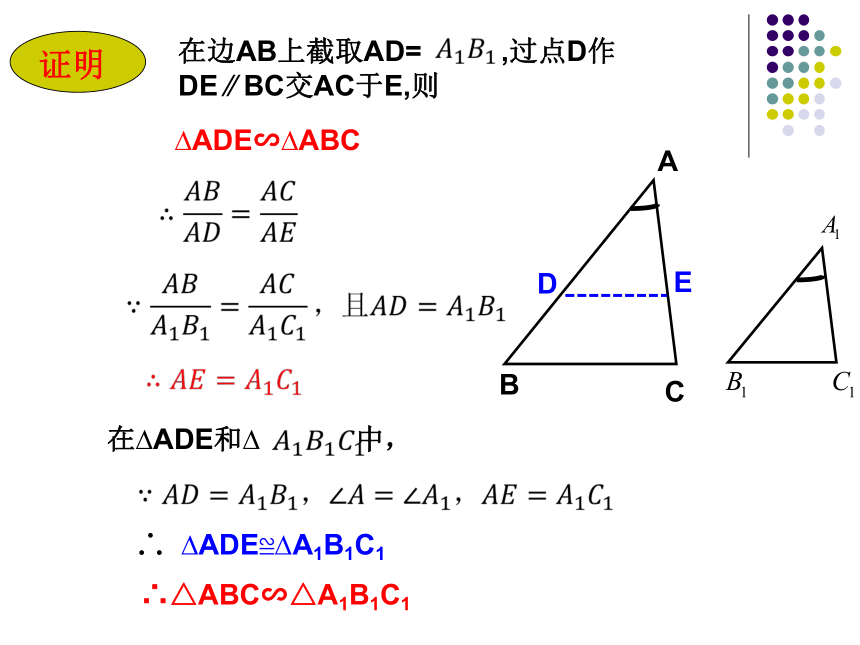
在边AB上截取AD= ,过点D作
DE ∕∕ BC交AC于E,则
?ADE∽?ABC
在?ADE和? 中,
∴△ABC∽△A1B1C1
?ADE≌?A1B1C1
知识概括
相似三角形 判定定理2:
两边成比例且夹角相等的两个角形相似。
3.2
3.2
G
C
50°
)
4
A
B
2
1.6
50°
)
E
D
F
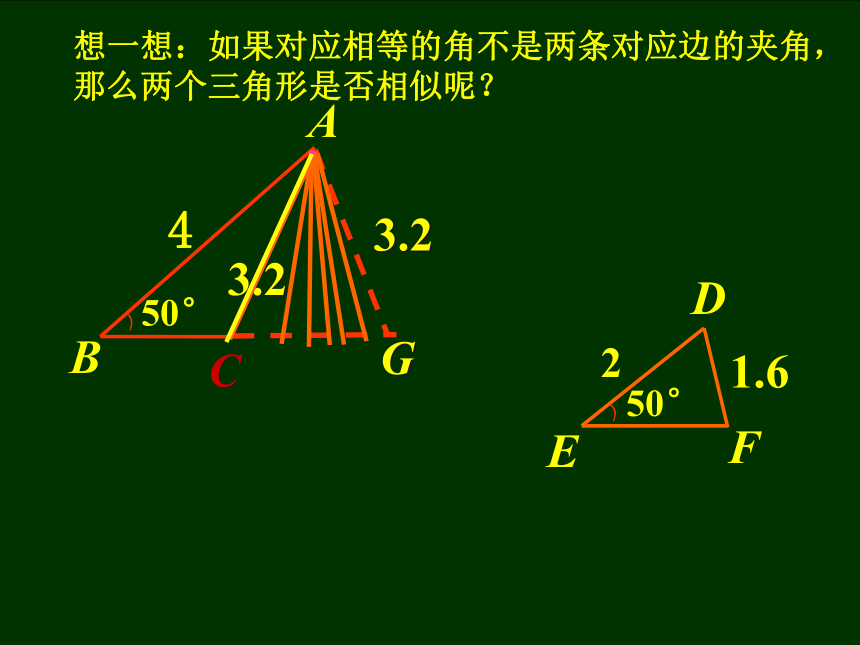
想一想:如果对应相等的角不是两条对应边的夹角,那么两个三角形是否相似呢?
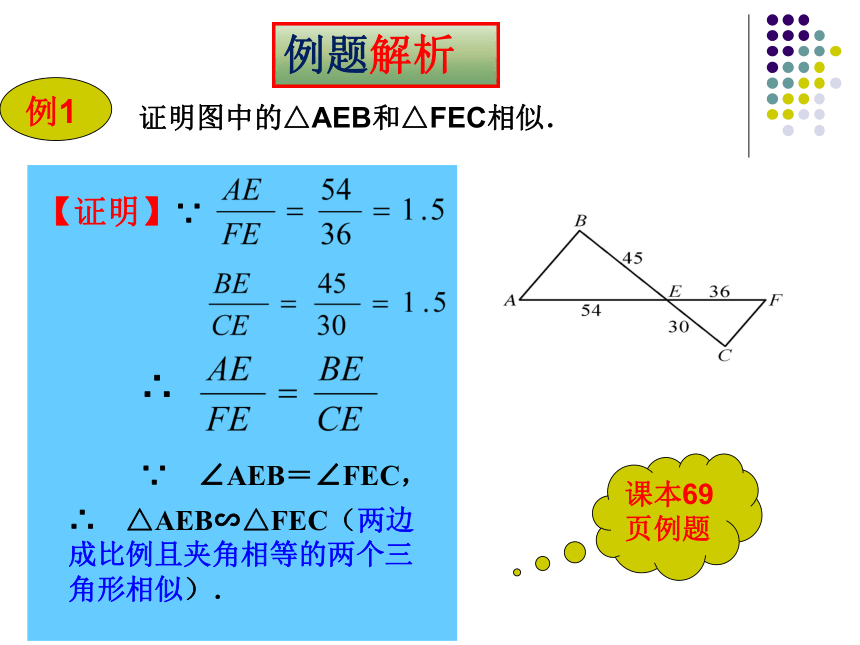
证明图中的△AEB和△FEC相似.
例题解析
例1
【证明】∵
∴
∵ ∠AEB=∠FEC,
∴ △AEB∽△FEC(两边成比例且夹角相等的两个三角形相似).
课本69页例题
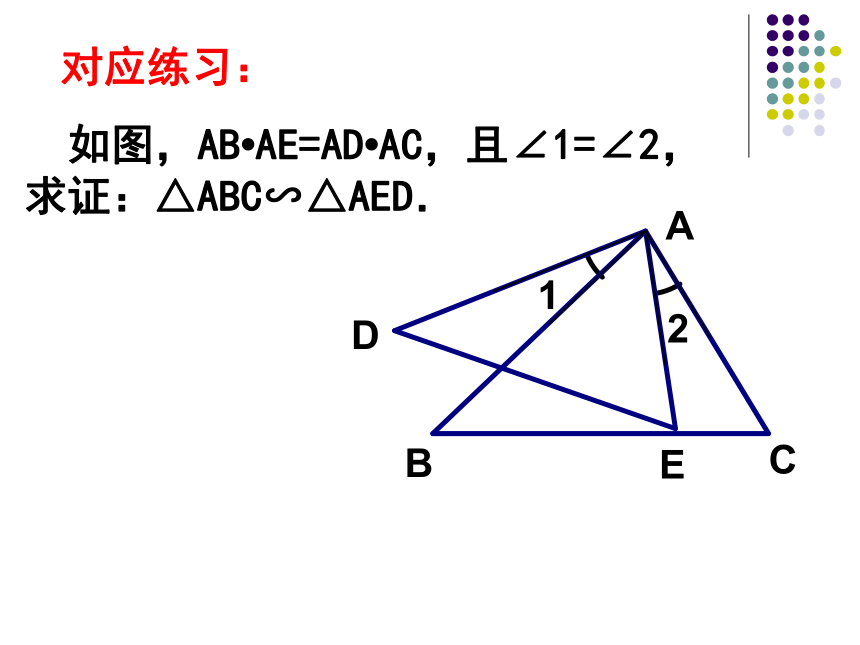
如图,AB?AE=AD?AC,且∠1=∠2,
求证:△ABC∽△AED.
对应练习:
例2
如图,在四边形ABCD中, AB=6,BC=4,AC=5,CD= ,求AD的长。
A
B
C
D
分析:
6
4
5
从图可知,已知两边及夹角,考虑两个三角形是否相似?
【解】
∵AB=6,BC=4,AC=5,CD=
∴?ABC∽?DCA
1.如图,在?ABC中,P是AC上的一点,连结BP,要使?ABP∽?ACB,则应添一个条件是:
______________________________________.
A
B
C
P
从图中可看出已经有了一个条件:
∠A是公共角,即∠BAP= ∠BAC
(1)如果用判定定理1:两角分别相等的两个三角形相似,则应添条件为:
∠ABP= ∠C,或
∠APB= ∠ABC
∠ABP= ∠C,或∠APB= ∠ABC,或
(2)如果用判定定理2:两边成比例且夹角相等的两个三角形相似,则应添的条件是:
对应练习:
2.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A
C
B
D
3.如图所示,在?ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有( )
A.3对 B.4对 C.5对 D.6对
4.如图,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,连接ED,图中的相似三角形的对数为( )
A.4对 B.6对 C.8对 D.9对
5.在正方形ABCD中,E为AD上的中点, F是AB的四分一等分点,连结EF、EC;△AEF与△DCE是否相似?说明理由.
6.已知:如图,△PCD是等边三角形,
∠APB = 120 °,你能发现几对三角形
相似?
P
D
C
B
A
7.如图,AB⊥BC,DC⊥BC,垂足分别为B、C,且AB=8,DC=6,BC=14,BC上是否存在点P使△ABP与△DCP相似?若有,有几个?并求出此时BP的长,若没有,请说明理由。
8
6
14
8.如图,在△ABC中,AB=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从点C出发,沿CA以3cm/s的速度向点A运动.设运动时间为ts.
P
Q
C
B
A
⑴PQ∥BC时,t为何值?
4t
3t
30-3t
20
P
Q
C
B
A
4t
3t
30-3t
20
⑵△APQ能否与△CQB相似?若能,求出AP的长;若不能,说明理由.
课堂小结
我们已经学习了三角形相似的判定:
方法1:平行线分三角形相似——平行于三角形一边的直线和两边(或两边的延长线)相交所构成的三角形和原三角形相似。
方法2:判定定理1——两角分别相等的两个三角形相似。
方法3:判定定理2——两边成比例且夹角相等的两个三角形相似。
再见
——判定2
知识回顾
三角形相似的判定方法:
平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似.
①平行线判定三角形相似:
②三角形相似的判定定理1:
两角分别相等的两个三角形相似。
知识探索
观察下图,如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE与△ABC相似呢?
图中两个三角形的一组对应边
AD与AB的长度的比值为_____.
将点E由点A开始在AC上移
动,可以发现当AE=
________AC时,△ADE与△ABC似乎相似.
此时,
E
猜想: 如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。
猜想证明
猜想: 如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。
已知:如图,在△ABC和 中,
求证:△ABC∽
C
A
B
分析:
D
E
这样,只考虑证明?ADE∽?ABC.
因为 所以,可把
移来与 重合,从而
?A1B1C1≌?ADE
C
A
B
证明
D
E
在边AB上截取AD= ,过点D作
DE ∕∕ BC交AC于E,则
?ADE∽?ABC
在?ADE和? 中,
∴△ABC∽△A1B1C1
?ADE≌?A1B1C1
知识概括
相似三角形 判定定理2:
两边成比例且夹角相等的两个角形相似。
3.2
3.2
G
C
50°
)
4
A
B
2
1.6
50°
)
E
D
F
想一想:如果对应相等的角不是两条对应边的夹角,那么两个三角形是否相似呢?
证明图中的△AEB和△FEC相似.
例题解析
例1
【证明】∵
∴
∵ ∠AEB=∠FEC,
∴ △AEB∽△FEC(两边成比例且夹角相等的两个三角形相似).
课本69页例题
如图,AB?AE=AD?AC,且∠1=∠2,
求证:△ABC∽△AED.
对应练习:
例2
如图,在四边形ABCD中, AB=6,BC=4,AC=5,CD= ,求AD的长。
A
B
C
D
分析:
6
4
5
从图可知,已知两边及夹角,考虑两个三角形是否相似?
【解】
∵AB=6,BC=4,AC=5,CD=
∴?ABC∽?DCA
1.如图,在?ABC中,P是AC上的一点,连结BP,要使?ABP∽?ACB,则应添一个条件是:
______________________________________.
A
B
C
P
从图中可看出已经有了一个条件:
∠A是公共角,即∠BAP= ∠BAC
(1)如果用判定定理1:两角分别相等的两个三角形相似,则应添条件为:
∠ABP= ∠C,或
∠APB= ∠ABC
∠ABP= ∠C,或∠APB= ∠ABC,或
(2)如果用判定定理2:两边成比例且夹角相等的两个三角形相似,则应添的条件是:
对应练习:
2.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A
C
B
D
3.如图所示,在?ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有( )
A.3对 B.4对 C.5对 D.6对
4.如图,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,连接ED,图中的相似三角形的对数为( )
A.4对 B.6对 C.8对 D.9对
5.在正方形ABCD中,E为AD上的中点, F是AB的四分一等分点,连结EF、EC;△AEF与△DCE是否相似?说明理由.
6.已知:如图,△PCD是等边三角形,
∠APB = 120 °,你能发现几对三角形
相似?
P
D
C
B
A
7.如图,AB⊥BC,DC⊥BC,垂足分别为B、C,且AB=8,DC=6,BC=14,BC上是否存在点P使△ABP与△DCP相似?若有,有几个?并求出此时BP的长,若没有,请说明理由。
8
6
14
8.如图,在△ABC中,AB=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从点C出发,沿CA以3cm/s的速度向点A运动.设运动时间为ts.
P
Q
C
B
A
⑴PQ∥BC时,t为何值?
4t
3t
30-3t
20
P
Q
C
B
A
4t
3t
30-3t
20
⑵△APQ能否与△CQB相似?若能,求出AP的长;若不能,说明理由.
课堂小结
我们已经学习了三角形相似的判定:
方法1:平行线分三角形相似——平行于三角形一边的直线和两边(或两边的延长线)相交所构成的三角形和原三角形相似。
方法2:判定定理1——两角分别相等的两个三角形相似。
方法3:判定定理2——两边成比例且夹角相等的两个三角形相似。
再见
