23.3相似三角形(4)判定3-华东师大版九年级数学上册课件(14张)
文档属性
| 名称 | 23.3相似三角形(4)判定3-华东师大版九年级数学上册课件(14张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览

文档简介
§23.3 相似三角形(4)
——判定3
知识回顾
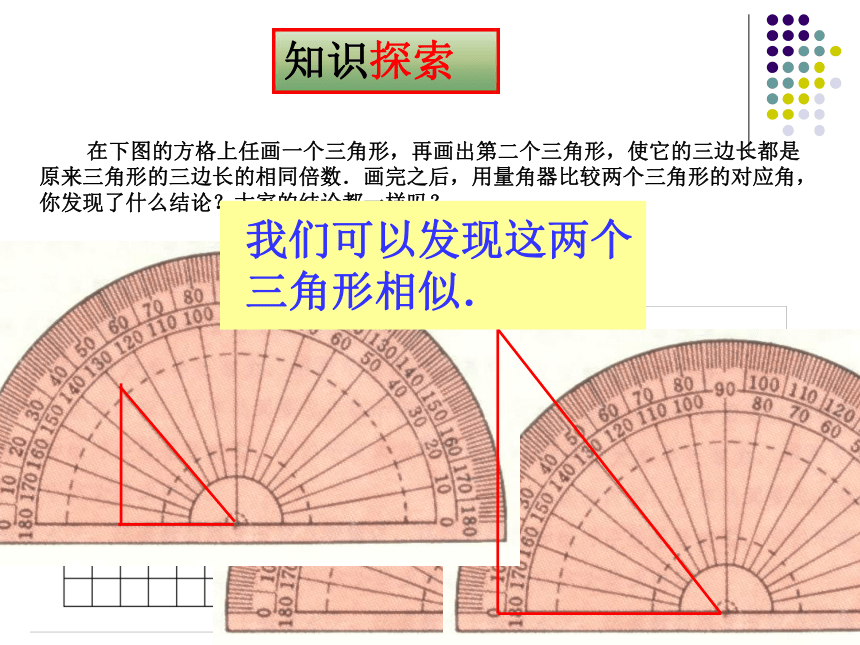
在下图的方格上任画一个三角形,再画出第二个三角形,使它的三边长都是原来三角形的三边长的相同倍数.画完之后,用量角器比较两个三角形的对应角,你发现了什么结论?大家的结论都一样吗?
我们可以发现这两个三角形相似.
知识探索
知识概括
相似三角形的判定定理3
三边成比例的两个三角形相似。
试试看,你能证明这个 定理吗?
A
B
C
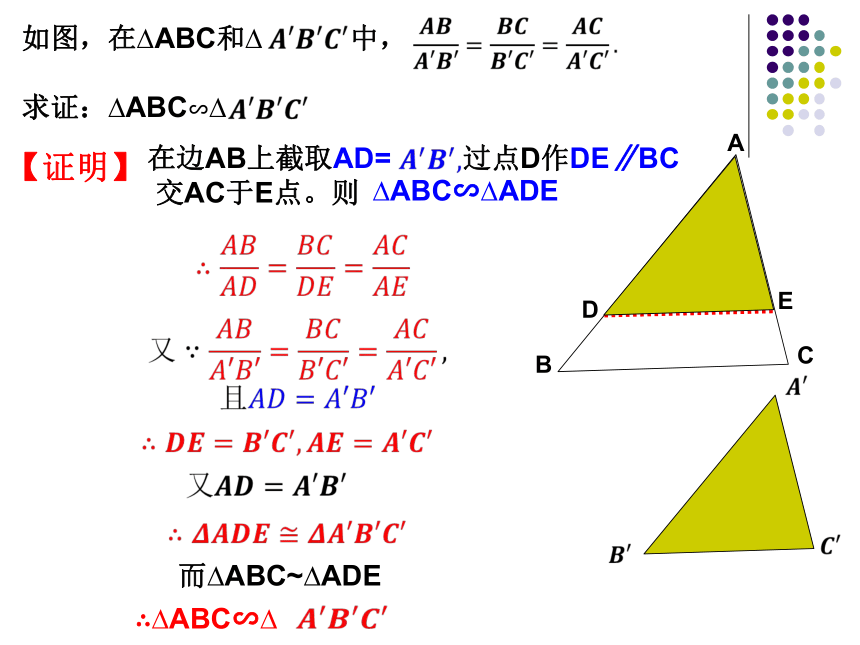
如图,在?ABC和? 中,
求证:?ABC∽?
D
E
【证明】
在边AB上截取AD= 过点D作DE∥BC
交AC于E点。则
?ABC∽?ADE
而?ABC~?ADE
∴?ABC∽?
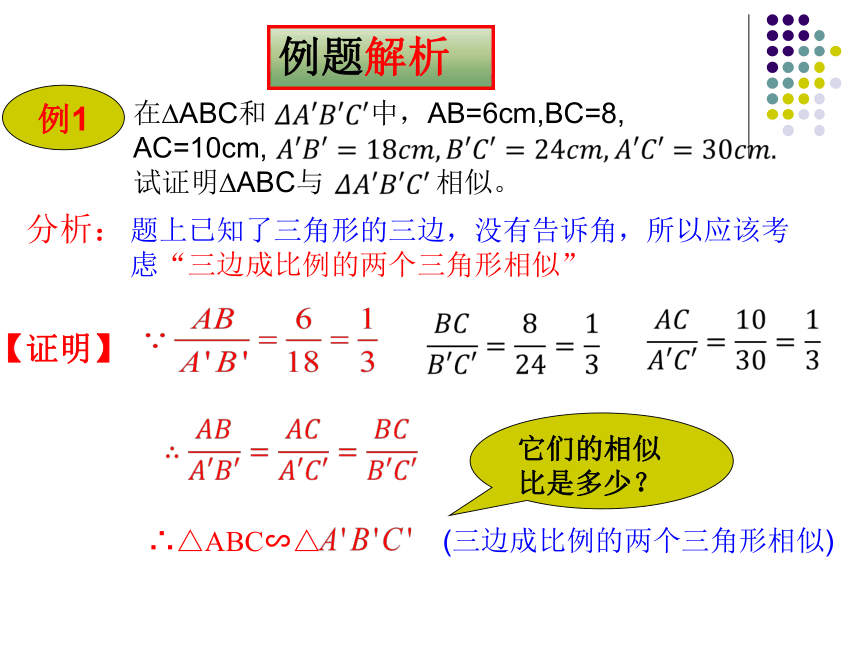
例1
例题解析
在?ABC和 中,AB=6cm,BC=8,
AC=10cm,
试证明?ABC与 相似。
分析:
题上已知了三角形的三边,没有告诉角,所以应该考虑“三边成比例的两个三角形相似”
【证明】
∴△ABC∽△
(三边成比例的两个三角形相似)
它们的相似比是多少?
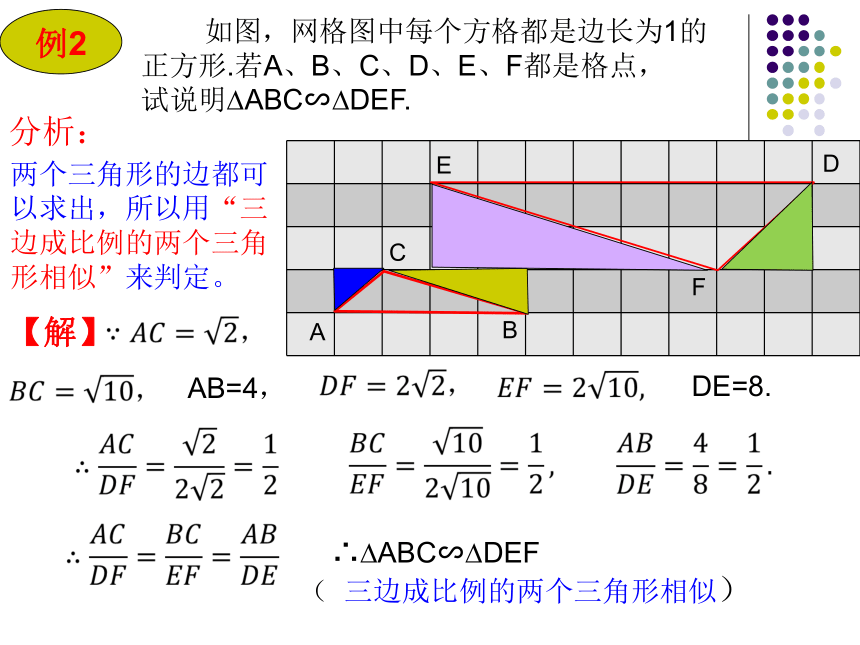
例2
如图,网格图中每个方格都是边长为1的正方形.若A、B、C、D、E、F都是格点,
试说明?ABC∽?DEF.
A
B
C
D
E
F
【解】
分析:
两个三角形的边都可以求出,所以用“三边成比例的两个三角形相似”来判定。
AB=4,
DE=8.
∴?ABC∽?DEF
( 三边成比例的两个三角形相似)
∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE
1.如图已知, 试说明∠BAD=∠CAE.
A
D
C
E
B
证明:
∵
课堂练习
运用3
答案是2:1
2、如图在正方形网格上有△A1B1C1和△A2B2C2,它们相似吗?如果相似,求出相似比;如果不相似,请说明理由。
方法2: 平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;
方法3: 两角相等的两个三角形相似.
相似三角形的判定方法
方法4:两边成比例且夹角相等的两个三角形相似.
方法1:通过定义(不常用)
方法5:、三边成比例的两个三角形相似.
课堂小结
(1)有一对等角,则可找另一对等角选判定1;或找夹这对等角的两边对应成比例选判定2.
(2)有两边对应成比例,则可找夹角相等选判定2;或找第三边成比例选判定3.
(3)已知等腰三角形,则可找顶角相等或底角相等选判定1;或找底和腰对应成比例选判定3.
(1)有平行线时选平行线截三角形相似。
练习巩固
1、依据下列各组条件,说明?ABC和? 是否相似:(课本70页练习)
(1)AB=10cm, BC=8cm, AC=16cm,
【解】
∴?ABC~?
注意边的对应关系:
常用小对小,大对大,中间对中间
的方法找对应边。
(2)∠A=80°, ∠C=60°, ∠A′=80°, ∠B′=40°.
【解】
∵ ∠A=80°, ∠C=60°
∴ ∠B=180°-80°-60°=40°
又∵ ∠A′=80°, ∠B′=40°.
∴ ∠A=∠A′, ∠B=∠B′
∴ ?ABC∽?A′B′C′( )
(3) ∠A=40°,AB=8,AC=15, ∠A′=40°,A′B′=16, A′C′=30.
【解】
又∵ ∠A= ∠A′=40°
∴ ?ABC∽?A′B′C′( )
两角分别相等的两个三角形相似
两边成比例且夹角相等的两个三角形相似
2、在第1题(3)中,若已知BC=a,∠B=α,你能求出B′C′的长和∠B′、∠C′的大小吗?写出你的计算过程。(课本70页练习)
【解】
∵ ?ABC∽?A′B′C′
∴ B′C′=2BC=2a.
——判定3
知识回顾
在下图的方格上任画一个三角形,再画出第二个三角形,使它的三边长都是原来三角形的三边长的相同倍数.画完之后,用量角器比较两个三角形的对应角,你发现了什么结论?大家的结论都一样吗?
我们可以发现这两个三角形相似.
知识探索
知识概括
相似三角形的判定定理3
三边成比例的两个三角形相似。
试试看,你能证明这个 定理吗?
A
B
C
如图,在?ABC和? 中,
求证:?ABC∽?
D
E
【证明】
在边AB上截取AD= 过点D作DE∥BC
交AC于E点。则
?ABC∽?ADE
而?ABC~?ADE
∴?ABC∽?
例1
例题解析
在?ABC和 中,AB=6cm,BC=8,
AC=10cm,
试证明?ABC与 相似。
分析:
题上已知了三角形的三边,没有告诉角,所以应该考虑“三边成比例的两个三角形相似”
【证明】
∴△ABC∽△
(三边成比例的两个三角形相似)
它们的相似比是多少?
例2
如图,网格图中每个方格都是边长为1的正方形.若A、B、C、D、E、F都是格点,
试说明?ABC∽?DEF.
A
B
C
D
E
F
【解】
分析:
两个三角形的边都可以求出,所以用“三边成比例的两个三角形相似”来判定。
AB=4,
DE=8.
∴?ABC∽?DEF
( 三边成比例的两个三角形相似)
∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE
1.如图已知, 试说明∠BAD=∠CAE.
A
D
C
E
B
证明:
∵
课堂练习
运用3
答案是2:1
2、如图在正方形网格上有△A1B1C1和△A2B2C2,它们相似吗?如果相似,求出相似比;如果不相似,请说明理由。
方法2: 平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;
方法3: 两角相等的两个三角形相似.
相似三角形的判定方法
方法4:两边成比例且夹角相等的两个三角形相似.
方法1:通过定义(不常用)
方法5:、三边成比例的两个三角形相似.
课堂小结
(1)有一对等角,则可找另一对等角选判定1;或找夹这对等角的两边对应成比例选判定2.
(2)有两边对应成比例,则可找夹角相等选判定2;或找第三边成比例选判定3.
(3)已知等腰三角形,则可找顶角相等或底角相等选判定1;或找底和腰对应成比例选判定3.
(1)有平行线时选平行线截三角形相似。
练习巩固
1、依据下列各组条件,说明?ABC和? 是否相似:(课本70页练习)
(1)AB=10cm, BC=8cm, AC=16cm,
【解】
∴?ABC~?
注意边的对应关系:
常用小对小,大对大,中间对中间
的方法找对应边。
(2)∠A=80°, ∠C=60°, ∠A′=80°, ∠B′=40°.
【解】
∵ ∠A=80°, ∠C=60°
∴ ∠B=180°-80°-60°=40°
又∵ ∠A′=80°, ∠B′=40°.
∴ ∠A=∠A′, ∠B=∠B′
∴ ?ABC∽?A′B′C′( )
(3) ∠A=40°,AB=8,AC=15, ∠A′=40°,A′B′=16, A′C′=30.
【解】
又∵ ∠A= ∠A′=40°
∴ ?ABC∽?A′B′C′( )
两角分别相等的两个三角形相似
两边成比例且夹角相等的两个三角形相似
2、在第1题(3)中,若已知BC=a,∠B=α,你能求出B′C′的长和∠B′、∠C′的大小吗?写出你的计算过程。(课本70页练习)
【解】
∵ ?ABC∽?A′B′C′
∴ B′C′=2BC=2a.
