北师大版九年级数学下册 3.6 直线和圆的位置关系 课件(27张)
文档属性
| 名称 | 北师大版九年级数学下册 3.6 直线和圆的位置关系 课件(27张) |  | |
| 格式 | ppt | ||
| 文件大小 | 426.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 19:11:20 | ||
图片预览






文档简介
复习提问:
1、点和圆的位置关系有哪几种?
2.怎样判定?
.A
. B
.C
点到圆心的距离为d,圆的半径为r,则:
点在圆外 d>r
点在圆上 d=r
点在圆内 d●O
观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的?
这个自然现象能否反映出直线与圆的位置关系?
地平线
第三章 圆
第五节 直线和圆的位置关系(一)
开发区第四中学
刘仲芹
直线与圆的位置关系
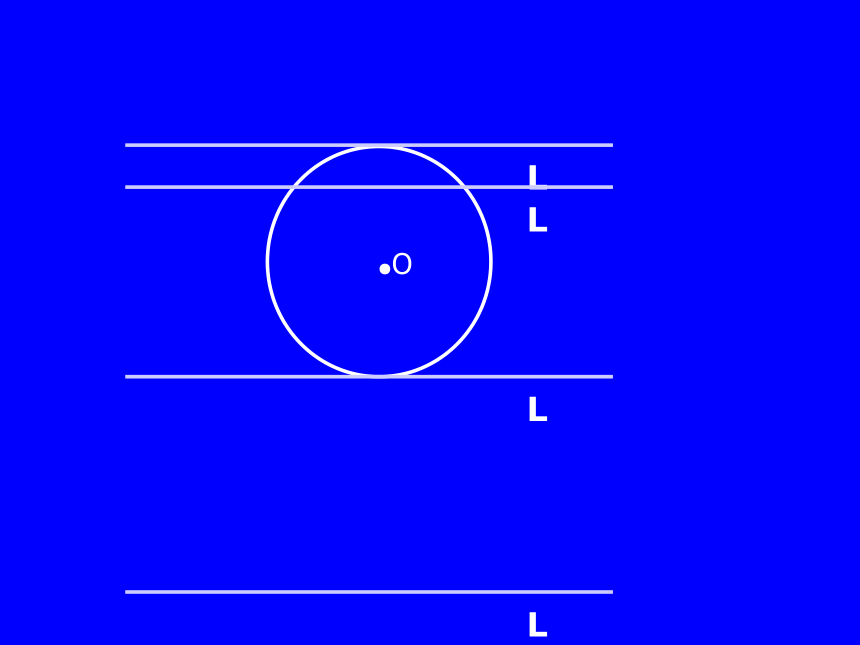
请同学们在纸上画一个圆,把手中的直尺或笔作为直线移动。观察:
(1)直线与圆公共点的个数各为多少?
(2)直线与圆的位置有哪几种可能?
试一试:
L
L
L
L
●O
.O
l
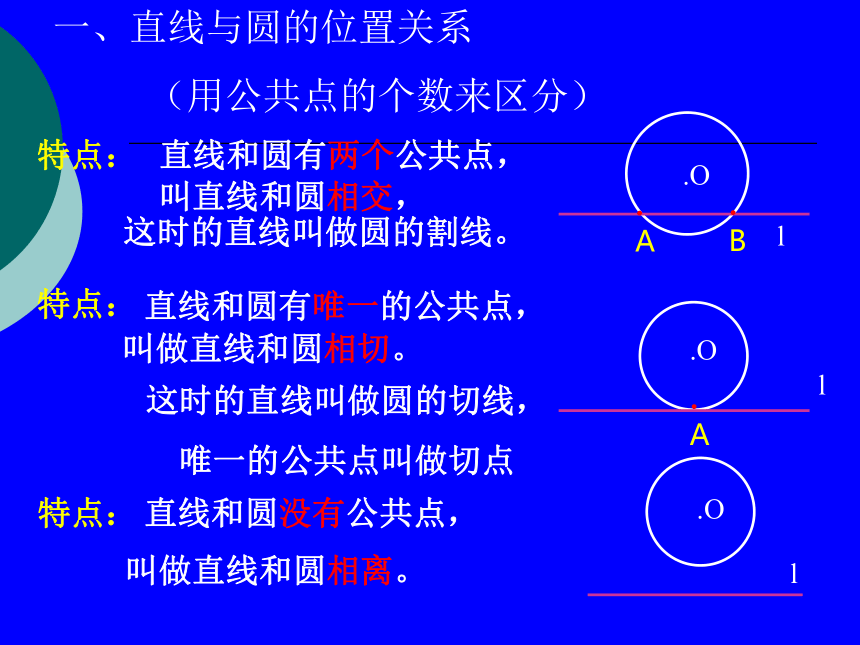
特点:
.O
叫做直线和圆相离。
直线和圆没有公共点,
l
特点:
直线和圆有唯一的公共点,
叫做直线和圆相切。
这时的直线叫做圆的切线,
唯一的公共点叫做切点
.O
l
特点:
直线和圆有两个公共点,
叫直线和圆相交,
这时的直线叫做圆的割线。
一、直线与圆的位置关系
(用公共点的个数来区分)
.A
.A
.B
运用:
相离
相切
相交
相交
l
l
2、看图判断直线l与 ⊙O的位置关系
(1)
(2)
(3)
(4)
l
l
·O
·O
·O
·O
1、你能举出生活中直线与圆相交、相切、相离的 实例吗?
(5)
?
l
如果有公共点,公共点的个数不好判断,该怎么办?
·O
“直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?
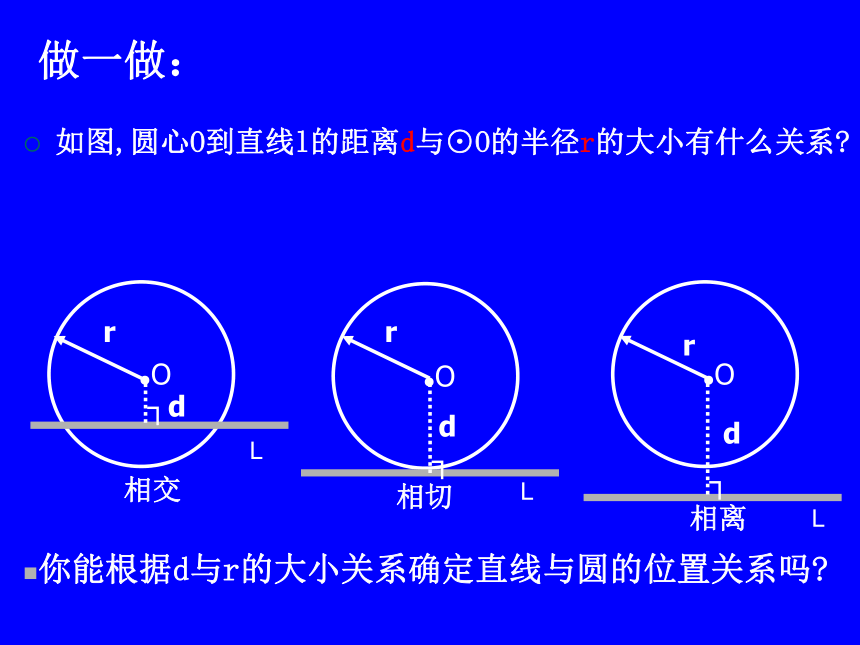
做一做:
如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系?
你能根据d与r的大小关系确定直线与圆的位置关系吗?
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
L
L
L
┐
d
r
.o
l
2、直线和圆相切
┐
d
r
d = r
.O
l
3、直线和圆相离
d > r
d
┐
r
.O
l
二、直线与圆的位置关系量化揭密
(用圆心o到直线l的距离d与圆的半径r的关系来区分)
1、直线和圆相交
d < r
相交
直线与圆的位置关系
公共点的个数
圆心到直线的距离d与半径r的关系
公共点的名称
直线名称
相切
相离
2
1
0
d<r
d=r
d>r
交点
切点
割线
切线
1、已知圆的直径为13cm,设圆心到直线的距离为d:
(1)若d=4.5cm,则d___r,直线与圆____直线与圆有_____个公共点。
(2)若d=6.5cm,则d___r,直线与圆__直线与圆有_____个公共点。
(3)若d=8cm,则d___r,直线与圆____直线与圆有____个公共点。
相交
2
相切
1
相离
0
巩固练习:
<
=
>
A.(-3,-4)
O
X
Y
B
C
4
3
2、已知⊙A的直径为6,点A的坐标为
(-3,-4),则⊙A与X轴的位置关系
是_____,⊙A与Y轴的位置关系是______。
相离
相切
例1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
B
A
C
┐
(2)以点C为圆心,分别以2cm,4cm为
半径作两个圆,这两个圆与AB分别有怎样
的位置关系?
∟
D
解:(1)过点C作CD⊥AB于D
A
C
B
┐
D
┛
根据面积相等得:
因此,当半径长为 cm时,AB与⊙C相切
根据勾股定理
∵AB=8cm,AC=4cm
(2)由(1)可知,圆心到AB的距离d= cm
∴当r=2cm时,d>r,AB与⊙C相离;
当r=4cm时,d变式训练.
B
A
C
┐
在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径的圆
与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm。
上面的三个图形是轴对称图形吗?如果是,你能画出它们的对称轴吗?
●O
●O
相交
●O
相切
相离
L
L
L
做一做:
如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说说你的理由.
直径AB垂直于直线CD.
C
D
B
●O
A
探索切线的性质
假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
探索切线的性质
则OM即d<r,
因此,CD与⊙O相交.
这与已知条件“直线CD与⊙O相切”相矛盾.
C
D
B
●O
A
所以AB与CD垂直.
M
┛
反证法
切线的性质定理:
圆的切线垂直于过切点的半径
∵直线CD切⊙O于点A
∴CD⊥OA
●O
C
D
A
A
B
C
.O
已知:如图,在两个同心圆中,大圆的弦AB切小圆于点C。
求证:点C是AB的中点
切线性质应用:
课堂小结:
本节课你有哪些收获?
你学会了哪些知识和方法?
2、判定直线 与圆的位置关系的方法有____种:
(1)由__________________的个数来判断;
(2)由___________________________ 的关系
来判断。
两
直线 与圆的公共点
圆心到直线的距离d与半径r
小结:
1、直线与圆的位置关系有哪几种:
相交 相切 相离
3、圆的切线的性质定理
圆的切线垂直于过切点的半径
达标检测
1.⊙O的半径是6,点O到直线a的距离为5,则直线置关系为( )
A.相离 B.相切 C.相交 D.内含
2.点A的坐标为(6,8),以点A为圆心,8为半径作圆A,则A与x轴、y轴、原点有怎样的位置关系?
3.已知Rt△ABC的斜边AB=6厘米,直角边AC为3厘米。
(1)以C为圆心,2厘米为半径的圆和AB的位置关系是 ;
(2)以C为圆心,4厘米为半径的圆和AB的位置关系是 ;
(3)若以C为圆心的圆和AB相切,则半径长为 ;
4.在△ABC中,已知∠C=90°,AB=5,AC=3,以C为圆心,以r为半径作圆,要使圆C与斜边AB有公共点,则r的取值范围是什么?
C
与X轴相切 与Y轴相交 原点在圆外
相离
相交
作业:
一、 预习:1、切线的判定定理
2、如何作三角形的内切圆
二、课后思考题一
1.已知:如图,P是⊙O外一点,PA,PB都是⊙O的切线,A,B是切点.请你观察猜想,PA,PB有怎样的数量关系?并证明你的结论.
●O
A
B
P
2.除(1)所得的结论外,你还能发现哪些新的结论?如果有,请你予以证明.
课外思考题二:已知点A的坐标为(1,3),⊙A的半径为4.
点O与⊙A分别有怎样的位置关系?
若⊙A与x轴有怎样的位置关系?
若要使⊙A与y轴相切,则要把⊙A向右平移几个单位?
(4)若要使⊙A与x轴、y轴都相切,则圆心A应当移到 什么位置?请写出点A所有可能位置的坐标.
1、点和圆的位置关系有哪几种?
2.怎样判定?
.A
. B
.C
点到圆心的距离为d,圆的半径为r,则:
点在圆外 d>r
点在圆上 d=r
点在圆内 d
观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的?
这个自然现象能否反映出直线与圆的位置关系?
地平线
第三章 圆
第五节 直线和圆的位置关系(一)
开发区第四中学
刘仲芹
直线与圆的位置关系
请同学们在纸上画一个圆,把手中的直尺或笔作为直线移动。观察:
(1)直线与圆公共点的个数各为多少?
(2)直线与圆的位置有哪几种可能?
试一试:
L
L
L
L
●O
.O
l
特点:
.O
叫做直线和圆相离。
直线和圆没有公共点,
l
特点:
直线和圆有唯一的公共点,
叫做直线和圆相切。
这时的直线叫做圆的切线,
唯一的公共点叫做切点
.O
l
特点:
直线和圆有两个公共点,
叫直线和圆相交,
这时的直线叫做圆的割线。
一、直线与圆的位置关系
(用公共点的个数来区分)
.A
.A
.B
运用:
相离
相切
相交
相交
l
l
2、看图判断直线l与 ⊙O的位置关系
(1)
(2)
(3)
(4)
l
l
·O
·O
·O
·O
1、你能举出生活中直线与圆相交、相切、相离的 实例吗?
(5)
?
l
如果有公共点,公共点的个数不好判断,该怎么办?
·O
“直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?
做一做:
如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系?
你能根据d与r的大小关系确定直线与圆的位置关系吗?
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
L
L
L
┐
d
r
.o
l
2、直线和圆相切
┐
d
r
d = r
.O
l
3、直线和圆相离
d > r
d
┐
r
.O
l
二、直线与圆的位置关系量化揭密
(用圆心o到直线l的距离d与圆的半径r的关系来区分)
1、直线和圆相交
d < r
相交
直线与圆的位置关系
公共点的个数
圆心到直线的距离d与半径r的关系
公共点的名称
直线名称
相切
相离
2
1
0
d<r
d=r
d>r
交点
切点
割线
切线
1、已知圆的直径为13cm,设圆心到直线的距离为d:
(1)若d=4.5cm,则d___r,直线与圆____直线与圆有_____个公共点。
(2)若d=6.5cm,则d___r,直线与圆__直线与圆有_____个公共点。
(3)若d=8cm,则d___r,直线与圆____直线与圆有____个公共点。
相交
2
相切
1
相离
0
巩固练习:
<
=
>
A.(-3,-4)
O
X
Y
B
C
4
3
2、已知⊙A的直径为6,点A的坐标为
(-3,-4),则⊙A与X轴的位置关系
是_____,⊙A与Y轴的位置关系是______。
相离
相切
例1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
B
A
C
┐
(2)以点C为圆心,分别以2cm,4cm为
半径作两个圆,这两个圆与AB分别有怎样
的位置关系?
∟
D
解:(1)过点C作CD⊥AB于D
A
C
B
┐
D
┛
根据面积相等得:
因此,当半径长为 cm时,AB与⊙C相切
根据勾股定理
∵AB=8cm,AC=4cm
(2)由(1)可知,圆心到AB的距离d= cm
∴当r=2cm时,d>r,AB与⊙C相离;
当r=4cm时,d
B
A
C
┐
在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径的圆
与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm。
上面的三个图形是轴对称图形吗?如果是,你能画出它们的对称轴吗?
●O
●O
相交
●O
相切
相离
L
L
L
做一做:
如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说说你的理由.
直径AB垂直于直线CD.
C
D
B
●O
A
探索切线的性质
假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
探索切线的性质
则OM
因此,CD与⊙O相交.
这与已知条件“直线CD与⊙O相切”相矛盾.
C
D
B
●O
A
所以AB与CD垂直.
M
┛
反证法
切线的性质定理:
圆的切线垂直于过切点的半径
∵直线CD切⊙O于点A
∴CD⊥OA
●O
C
D
A
A
B
C
.O
已知:如图,在两个同心圆中,大圆的弦AB切小圆于点C。
求证:点C是AB的中点
切线性质应用:
课堂小结:
本节课你有哪些收获?
你学会了哪些知识和方法?
2、判定直线 与圆的位置关系的方法有____种:
(1)由__________________的个数来判断;
(2)由___________________________ 的关系
来判断。
两
直线 与圆的公共点
圆心到直线的距离d与半径r
小结:
1、直线与圆的位置关系有哪几种:
相交 相切 相离
3、圆的切线的性质定理
圆的切线垂直于过切点的半径
达标检测
1.⊙O的半径是6,点O到直线a的距离为5,则直线置关系为( )
A.相离 B.相切 C.相交 D.内含
2.点A的坐标为(6,8),以点A为圆心,8为半径作圆A,则A与x轴、y轴、原点有怎样的位置关系?
3.已知Rt△ABC的斜边AB=6厘米,直角边AC为3厘米。
(1)以C为圆心,2厘米为半径的圆和AB的位置关系是 ;
(2)以C为圆心,4厘米为半径的圆和AB的位置关系是 ;
(3)若以C为圆心的圆和AB相切,则半径长为 ;
4.在△ABC中,已知∠C=90°,AB=5,AC=3,以C为圆心,以r为半径作圆,要使圆C与斜边AB有公共点,则r的取值范围是什么?
C
与X轴相切 与Y轴相交 原点在圆外
相离
相交
作业:
一、 预习:1、切线的判定定理
2、如何作三角形的内切圆
二、课后思考题一
1.已知:如图,P是⊙O外一点,PA,PB都是⊙O的切线,A,B是切点.请你观察猜想,PA,PB有怎样的数量关系?并证明你的结论.
●O
A
B
P
2.除(1)所得的结论外,你还能发现哪些新的结论?如果有,请你予以证明.
课外思考题二:已知点A的坐标为(1,3),⊙A的半径为4.
点O与⊙A分别有怎样的位置关系?
若⊙A与x轴有怎样的位置关系?
若要使⊙A与y轴相切,则要把⊙A向右平移几个单位?
(4)若要使⊙A与x轴、y轴都相切,则圆心A应当移到 什么位置?请写出点A所有可能位置的坐标.
