沪教版(上海)初中数学九年级第一学期 24.5相似三角形性质(1) 课件(16张)
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 24.5相似三角形性质(1) 课件(16张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 132.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 19:22:38 | ||
图片预览





文档简介
相似三角形性质(1)
复习引入:
对应角相等,对应边成比例的两个三角形叫做相似三角形。相似三角形对应边的比叫相似比。
1.什么叫相似三角形?相似比?
2.根据定义可知,相似三角形有哪些性质?
相似三角形的对应角相等,对应边成比例。
学习目标:
1,理解并掌握相似三角形对应高的比、对应中线
的比、对应角平分线的比都等于相似比的性质;
2,会用相似三角形的性质解决简单的实际问题 。
1,相似三角形的性质定理1的内容是什么?
你能把它改成三个命题吗?你是如何证明的?
2,如图所示,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm.要把它加工成矩形零件,使矩形的长,宽之比为2:1,并且矩形长的一边位于边BC上,另两个顶点分别在边AB,AC上,求这个矩形零件的长和宽.
自学提纲:
阅读书本上第87页内容和第88页例1,解决以下问题:
合作探究:
●相似三角形的对应边上的中线比等于相似比.
●相似三角形的对应边上的高的比等于相似比.
●相似三角形的对应角的角平分线的比等于相似比.
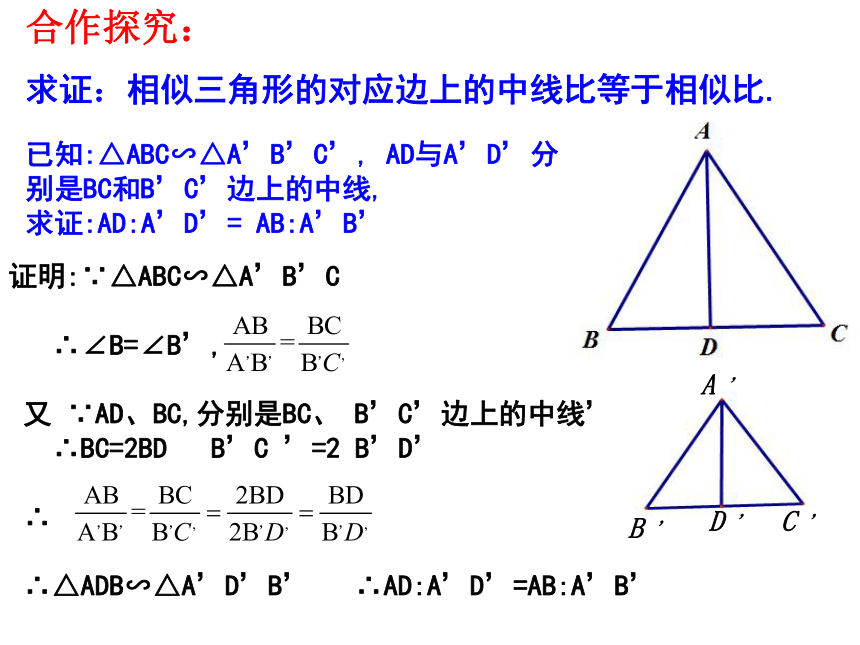
求证:相似三角形的对应边上的中线比等于相似比.
合作探究:
A ,
B ,
C ,
D ,
已知:△ABC∽△A’B’C’, AD与A’D’分别是BC和B’C’边上的中线,
求证:AD:A’D’= AB:A’B’
证明:∵△ABC∽△A’B’C
∴∠B=∠B’,
又 ∵AD、BC,分别是BC、 B’C’边上的中线’
∴BC=2BD B’C ’=2 B’D’
∴
∴△ADB∽△A’D’B’ ∴AD:A’D’=AB:A’B’
归纳:
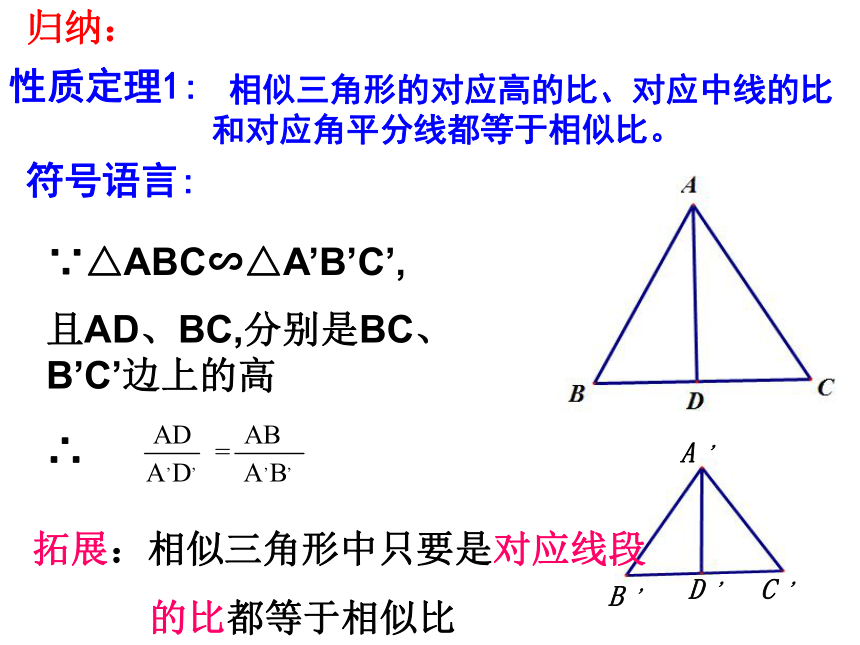
相似三角形的对应高的比、对应中线的比和对应角平分线都等于相似比。
性质定理1:
A ,
B ,
C ,
D ,
∵△ABC∽△A’B’C’,
且AD、BC,分别是BC、
B’C’边上的高
符号语言:
∴
拓展:相似三角形中只要是对应线段
的比都等于相似比
课堂练习:
已知△ABC∽△A’B’C’,BC=3.6㎝,B’C’=6㎝,AE是△ABC的一条中线,AE=2.4㎝,则△A’B’C’中对应中线A’E’是多少?
答:这个矩形零件的长和宽分别
是48cm和24cm。
理解应用
2.一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm.
要把它加工成矩形零件,使矩形的长,宽之比为2:1,
并且矩形长的一边位于边BC上,另两个顶点分别在边
AB,AC上,求这个矩形零件的长和宽.
如图内接矩形PQRS,其长边SR在BC上,顶点P、Q分别在AB、AC 上,△ABC的高AD交PQ边于点E,由题意设PS为xcm,则PQ为2xcm.
解:
P
Q
R
s
E
变式题:块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm,矩形PQRS的顶点P,Q分别在AB和AC边上,R,S在BC边上,当各边长长是多少时,矩形PQRS的面积最大?最大面积是多少?
1、相似三角形的性质:
①定义:相似三角形对应角相等,对应边成比例
②性质定理1:相似三角形的对应高的比、对应中线的比
和对应角平分线都等于相似比。
课堂总结
2、类比的学习方法和转化的数学思想。
本节课你有什么收获?
必做题:书本上第90页课后练习第2题。
选做题:已知如图,△ABC中∠ACB=90°,
AD⊥AB于点D,AE是∠CAB的平分线,
交CD于点F,交CB于点E。
求证:
布置作业:
课堂
作业
课外
作业
必做题:基训第65页第6题,第69页第7题。
选做题:基训第70页第7题。
如图,一条河流的两岸有一段是平行的,在河的北岸每隔50米有一根电线杆,我站在离南岸边15米的点P看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且这两棵树之间还有三棵树,我能知道河的宽度吗?
情景引入:
P
S
Q
R
E
证明:∵△ABC∽△A’B’C’,且相似比为k,
∴∠B=∠B’,
∵AD、BC,分别是BC、 B’C’边上的中线’
∴BC=2BD B’D’=2 B’C’
∴△ADB∽△A’D’B’
∴AD:A’D’=AB:A’B’=k
1.求证:相似三角形的对应高的比等于相似比.
已知:△ABC∽△A’B’C’,相似比为k,
AD与A’D’分别是BC和B’C’边上的高,
求证:AD:A’D’= AB:A’B’= k
证明:∵△ABC∽△A’B’C’,且相似比为k,
∴∠B=∠B’,AB:A’B’=k
∵AD⊥BC,A’D’⊥B’C’
∴∠ADB=∠A’D’B’=90°
∴△ADB∽△A’D’B’
∴AD:A’D’=AB:A’B’=k
合作探究:
2.求证:相似三角形的对应边上的中线的比等于相似比.
3.求证:相似三角形的对应角的平分线的比等于相似比.
你能从以下的词语中选择一个或两个,结合本节课的
学习进行一个总结回顾吗?
收获,方法,思想,疑惑,
感悟与反思:
复习引入:
对应角相等,对应边成比例的两个三角形叫做相似三角形。相似三角形对应边的比叫相似比。
1.什么叫相似三角形?相似比?
2.根据定义可知,相似三角形有哪些性质?
相似三角形的对应角相等,对应边成比例。
学习目标:
1,理解并掌握相似三角形对应高的比、对应中线
的比、对应角平分线的比都等于相似比的性质;
2,会用相似三角形的性质解决简单的实际问题 。
1,相似三角形的性质定理1的内容是什么?
你能把它改成三个命题吗?你是如何证明的?
2,如图所示,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm.要把它加工成矩形零件,使矩形的长,宽之比为2:1,并且矩形长的一边位于边BC上,另两个顶点分别在边AB,AC上,求这个矩形零件的长和宽.
自学提纲:
阅读书本上第87页内容和第88页例1,解决以下问题:
合作探究:
●相似三角形的对应边上的中线比等于相似比.
●相似三角形的对应边上的高的比等于相似比.
●相似三角形的对应角的角平分线的比等于相似比.
求证:相似三角形的对应边上的中线比等于相似比.
合作探究:
A ,
B ,
C ,
D ,
已知:△ABC∽△A’B’C’, AD与A’D’分别是BC和B’C’边上的中线,
求证:AD:A’D’= AB:A’B’
证明:∵△ABC∽△A’B’C
∴∠B=∠B’,
又 ∵AD、BC,分别是BC、 B’C’边上的中线’
∴BC=2BD B’C ’=2 B’D’
∴
∴△ADB∽△A’D’B’ ∴AD:A’D’=AB:A’B’
归纳:
相似三角形的对应高的比、对应中线的比和对应角平分线都等于相似比。
性质定理1:
A ,
B ,
C ,
D ,
∵△ABC∽△A’B’C’,
且AD、BC,分别是BC、
B’C’边上的高
符号语言:
∴
拓展:相似三角形中只要是对应线段
的比都等于相似比
课堂练习:
已知△ABC∽△A’B’C’,BC=3.6㎝,B’C’=6㎝,AE是△ABC的一条中线,AE=2.4㎝,则△A’B’C’中对应中线A’E’是多少?
答:这个矩形零件的长和宽分别
是48cm和24cm。
理解应用
2.一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm.
要把它加工成矩形零件,使矩形的长,宽之比为2:1,
并且矩形长的一边位于边BC上,另两个顶点分别在边
AB,AC上,求这个矩形零件的长和宽.
如图内接矩形PQRS,其长边SR在BC上,顶点P、Q分别在AB、AC 上,△ABC的高AD交PQ边于点E,由题意设PS为xcm,则PQ为2xcm.
解:
P
Q
R
s
E
变式题:块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm,矩形PQRS的顶点P,Q分别在AB和AC边上,R,S在BC边上,当各边长长是多少时,矩形PQRS的面积最大?最大面积是多少?
1、相似三角形的性质:
①定义:相似三角形对应角相等,对应边成比例
②性质定理1:相似三角形的对应高的比、对应中线的比
和对应角平分线都等于相似比。
课堂总结
2、类比的学习方法和转化的数学思想。
本节课你有什么收获?
必做题:书本上第90页课后练习第2题。
选做题:已知如图,△ABC中∠ACB=90°,
AD⊥AB于点D,AE是∠CAB的平分线,
交CD于点F,交CB于点E。
求证:
布置作业:
课堂
作业
课外
作业
必做题:基训第65页第6题,第69页第7题。
选做题:基训第70页第7题。
如图,一条河流的两岸有一段是平行的,在河的北岸每隔50米有一根电线杆,我站在离南岸边15米的点P看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且这两棵树之间还有三棵树,我能知道河的宽度吗?
情景引入:
P
S
Q
R
E
证明:∵△ABC∽△A’B’C’,且相似比为k,
∴∠B=∠B’,
∵AD、BC,分别是BC、 B’C’边上的中线’
∴BC=2BD B’D’=2 B’C’
∴△ADB∽△A’D’B’
∴AD:A’D’=AB:A’B’=k
1.求证:相似三角形的对应高的比等于相似比.
已知:△ABC∽△A’B’C’,相似比为k,
AD与A’D’分别是BC和B’C’边上的高,
求证:AD:A’D’= AB:A’B’= k
证明:∵△ABC∽△A’B’C’,且相似比为k,
∴∠B=∠B’,AB:A’B’=k
∵AD⊥BC,A’D’⊥B’C’
∴∠ADB=∠A’D’B’=90°
∴△ADB∽△A’D’B’
∴AD:A’D’=AB:A’B’=k
合作探究:
2.求证:相似三角形的对应边上的中线的比等于相似比.
3.求证:相似三角形的对应角的平分线的比等于相似比.
你能从以下的词语中选择一个或两个,结合本节课的
学习进行一个总结回顾吗?
收获,方法,思想,疑惑,
感悟与反思:
