沪教版(上海)初中数学九年级第一学期24.4(4)相似三角形的判定课件(18张)
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期24.4(4)相似三角形的判定课件(18张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 206.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 23:38:39 | ||
图片预览



文档简介
24.4(4)相似三角形的判定
相似三角形的判定方法
知识回顾
?
两个直角三角形一定相似吗?
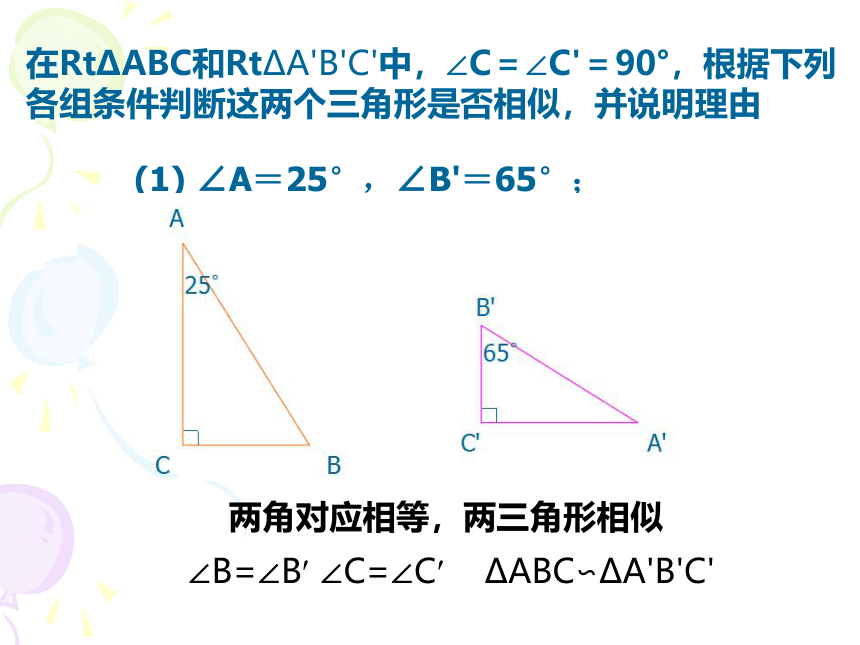
在RtΔABC和RtΔA'B'C'中,∠C=∠C'=90°,根据下列各组条件判断这两个三角形是否相似,并说明理由
(1) ∠A=25°,∠B'=65°;
∠B=∠B? ∠C=∠C? ΔABC∽ΔA'B'C'
两角对应相等,两三角形相似
( 2 ) AC=3,BC=4,A'C'=6,B'C'=8
两边对应成比例且夹角相等,两三角形相似
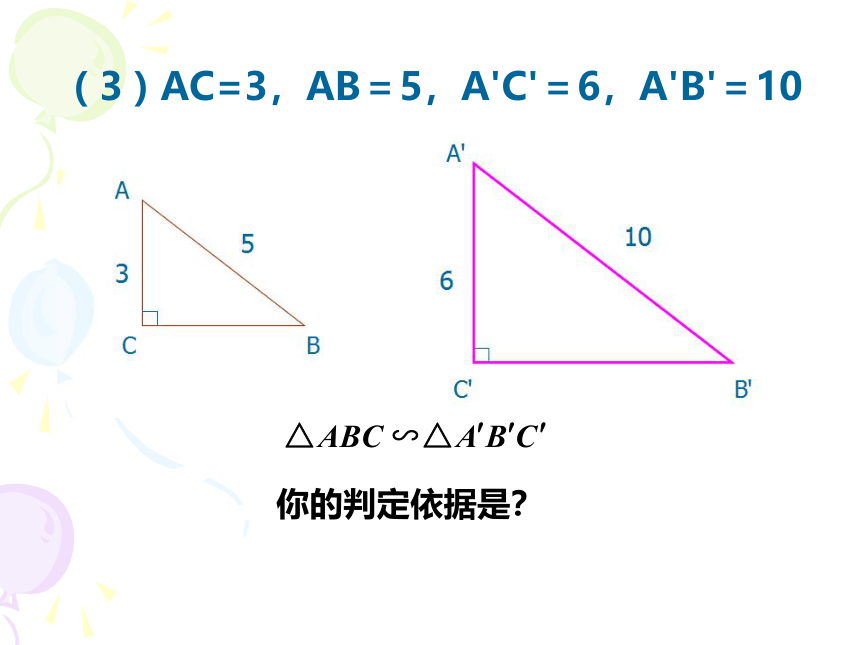
( 3 ) AC=3,AB=5,A'C'=6,A'B'=10
你的判定依据是?
思考:
直角三角形全等的判定
直角三角形相似的判定
HL
猜想:斜边和一条直角边对应成比例,
两直角三角形相似
斜边和一条直角边对应相等,
两直角三角形全等
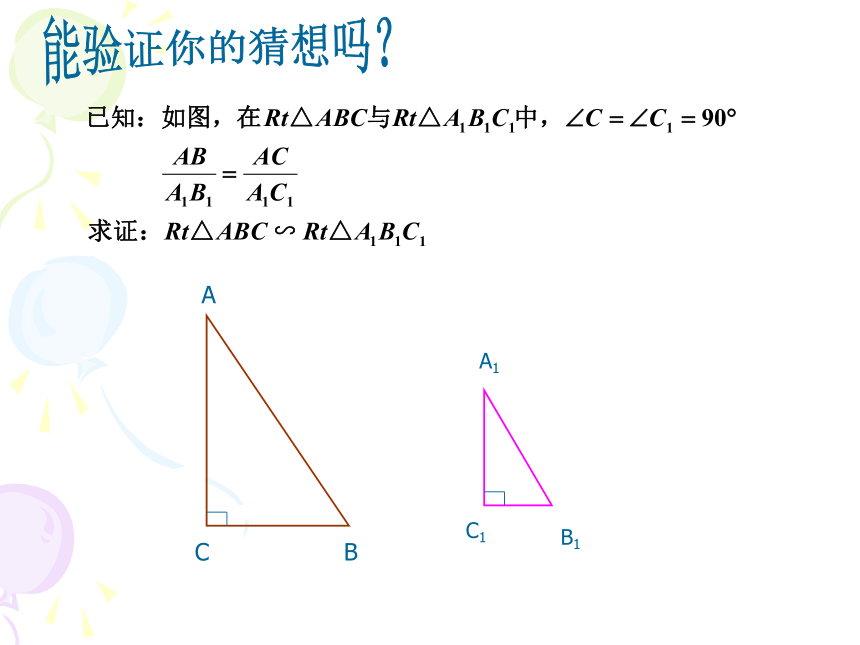
能验证你的猜想吗?
B
A
C
A1
B1
C1
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三形相似。
直角三角形相似判定方法
简单地说:
斜边和直角边对应成比例,两直角三角形相似。
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列两个直角三角形是否相似?
(1)
看一看
A
C
B
D
F
E
4
5
12
15
(2)
A
C
B
D
F
E
3
5
12
15
(3)
B
A
C
D
F
E
5
4
15
12
已知:如图,在四边形ABCD中,
求证:
例题讲解
练习:在 中,
求证:
课堂小结
直角三角形相似的判定方法:
(判定定理1)两角对应相等
(判定定理2)两边对应成比例且夹角相等
(判定定理3)三边对应成比例
(特殊)斜边和直角边对应成比例
预备定理
有一锐角相等的两Rt△相似
必做题:习题册24.4(4)
选做题:作业单
布置作业
拓展
1.已知:在RtΔABC中,CD是斜边AB上的高,E是BC
上的一点,AE交CD于点F,AE?AD=AF?AC,
求证:(1) AE是∠CAB的平分线
(2) AB?AF=AC?AE
2. 已知:在RtΔABC中, ∠C=90°,CD是AB边上的高
求证: (1)
(2)
相似三角形的判定方法
知识回顾
?
两个直角三角形一定相似吗?
在RtΔABC和RtΔA'B'C'中,∠C=∠C'=90°,根据下列各组条件判断这两个三角形是否相似,并说明理由
(1) ∠A=25°,∠B'=65°;
∠B=∠B? ∠C=∠C? ΔABC∽ΔA'B'C'
两角对应相等,两三角形相似
( 2 ) AC=3,BC=4,A'C'=6,B'C'=8
两边对应成比例且夹角相等,两三角形相似
( 3 ) AC=3,AB=5,A'C'=6,A'B'=10
你的判定依据是?
思考:
直角三角形全等的判定
直角三角形相似的判定
HL
猜想:斜边和一条直角边对应成比例,
两直角三角形相似
斜边和一条直角边对应相等,
两直角三角形全等
能验证你的猜想吗?
B
A
C
A1
B1
C1
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三形相似。
直角三角形相似判定方法
简单地说:
斜边和直角边对应成比例,两直角三角形相似。
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列两个直角三角形是否相似?
(1)
看一看
A
C
B
D
F
E
4
5
12
15
(2)
A
C
B
D
F
E
3
5
12
15
(3)
B
A
C
D
F
E
5
4
15
12
已知:如图,在四边形ABCD中,
求证:
例题讲解
练习:在 中,
求证:
课堂小结
直角三角形相似的判定方法:
(判定定理1)两角对应相等
(判定定理2)两边对应成比例且夹角相等
(判定定理3)三边对应成比例
(特殊)斜边和直角边对应成比例
预备定理
有一锐角相等的两Rt△相似
必做题:习题册24.4(4)
选做题:作业单
布置作业
拓展
1.已知:在RtΔABC中,CD是斜边AB上的高,E是BC
上的一点,AE交CD于点F,AE?AD=AF?AC,
求证:(1) AE是∠CAB的平分线
(2) AB?AF=AC?AE
2. 已知:在RtΔABC中, ∠C=90°,CD是AB边上的高
求证: (1)
(2)
