华东师大版九年级数学下册课件:27.1 .2 圆的对称性(34张)
文档属性
| 名称 | 华东师大版九年级数学下册课件:27.1 .2 圆的对称性(34张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 23:45:42 | ||
图片预览







文档简介
27.1 .2 圆的对称性
情境导入
熊宝宝要过生日了!要把蛋糕平均分成四块,你会分吗?
获取新知
问题1 圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
问题2 你是怎么得出结论的?
用折叠的方法
●O
圆的对称性1:
圆是轴对称图形,其对称轴是直径所在的直线
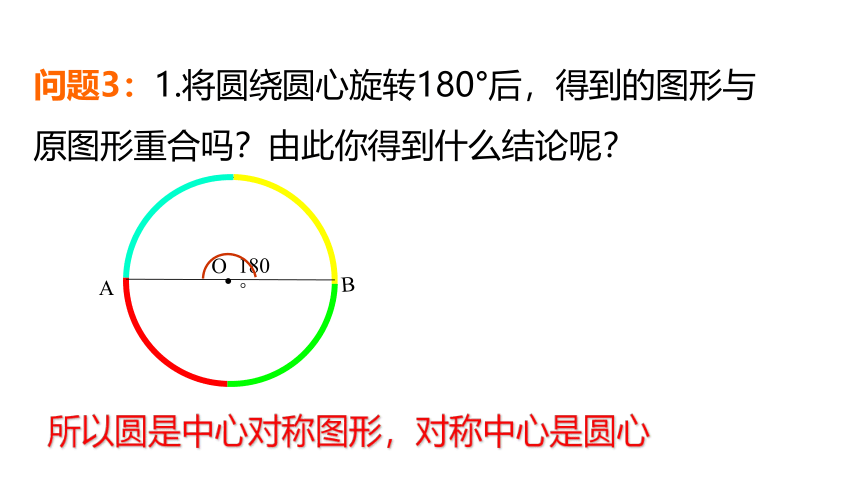
问题3:1.将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
.
O
A
B
180°
所以圆是中心对称图形,对称中心是圆心
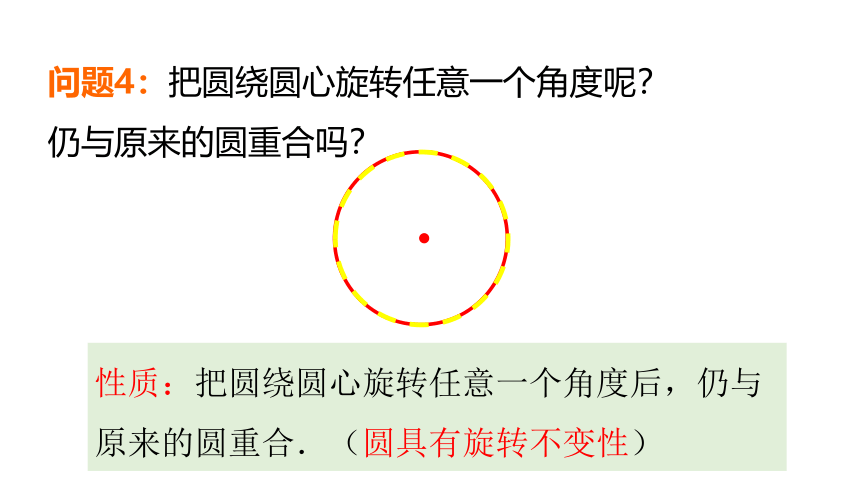
问题4:把圆绕圆心旋转任意一个角度呢?
仍与原来的圆重合吗?
·
性质:把圆绕圆心旋转任意一个角度后,仍与原来的圆重合.(圆具有旋转不变性)
圆心角:我们把顶点在圆心的角叫做圆心角.
·
O
B
A
∠AOB为圆心角
圆心角∠AOB所对的弦为AB,所对的弧为AB.
⌒
在同圆中探究
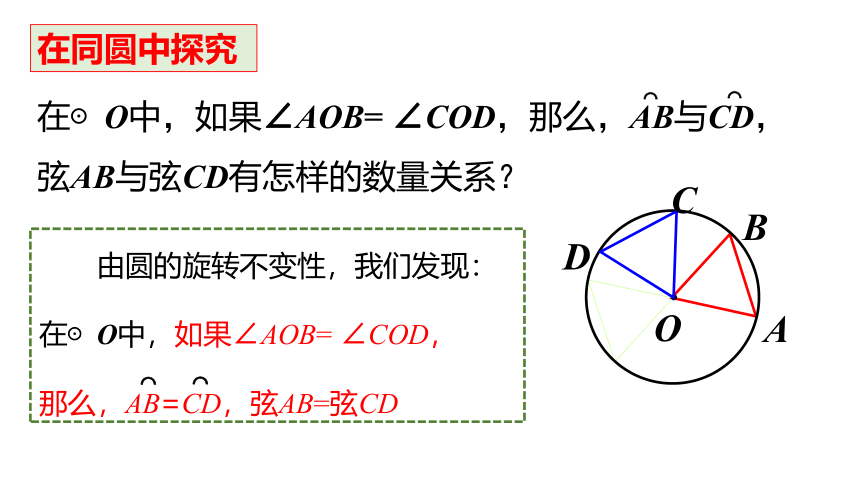
在⊙O中,如果∠AOB= ∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
⌒
·
O
A
B
C
D
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠COD,
那么,AB=CD,弦AB=弦CD
⌒
⌒
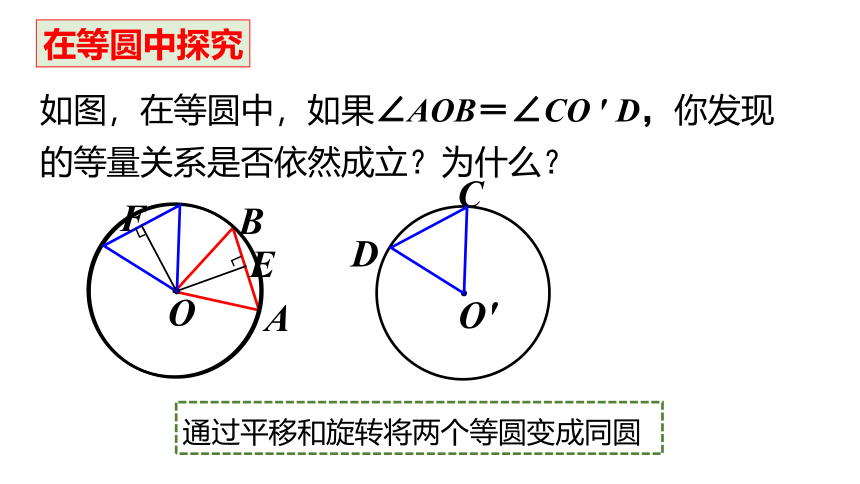
在等圆中探究
如图,在等圆中,如果∠AOB=∠CO ′ D,你发现的等量关系是否依然成立?为什么?
·
O
A
B
C
·
O'
D
通过平移和旋转将两个等圆变成同圆
┐
E
·
┐
F
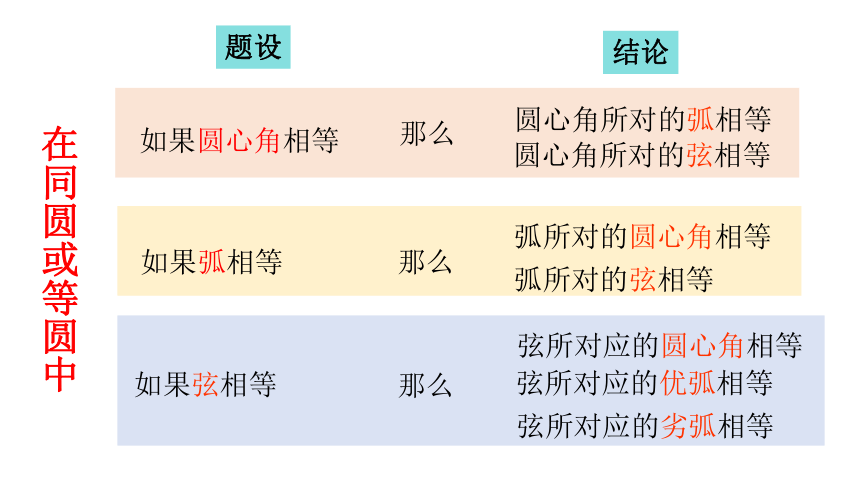
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
在同圆或等圆中
题设
结论
例题讲解
解:
∵
例1 如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
随堂演练
1.如果两个圆心角相等,那么 ( )
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
2.弦长等于半径的弦所对的圆心角等于 .
D
60 °
3.在同圆中,圆心角∠AOB=2∠COD,则AB与CD的关系是( )
⌒ ⌒
A
A. AB=2CD
⌒ ⌒
B. AB>CD
⌒ ⌒
C. AB⌒ ⌒
D. 不能确定
课堂小结
圆心角
圆心角
相等
弧
相等
弦
相等
弦、弧、圆心角的关系定理
在同圆或等圆中
概念:顶点在圆心的角
应用提醒
①要注意前提条件;
②要灵活转化.
27.1.2 圆的对称性
第2课时 垂径定理
情景导入
问题:你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m,你能求出赵州桥主桥拱的半径吗?
获取新知
如图, AB是⊙O的一条弦,作直径CD,使CD丄AB,垂足为P.
(1)图是轴对称图形吗?如果是,
其对称轴是什么?
(2)你能发现图中有哪些等量关
系?说一说你的理由.
(1)此图是轴对称图形,对称轴是直径CD所在的直线
(2)AP=BP, AC=BC,AD=BD
⌒
⌒
⌒
⌒
已知:在☉O中,CD是直径,AB是弦,AB⊥CD,垂足为P. 求证:AP=BP, AC =BC,AD =BD.
⌒
⌒
⌒
⌒
证明:连接OA、OB、CA、CB,则OA=OB.
即△AOB是等腰三角形.
∵AB⊥CD,
∴AP=BP,∠AOC=∠BOC.
⌒
⌒
AC =BC.
∴AD =BD
⌒
⌒
从而∠AOD=∠BOD.
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
用几何语言表述为:
∵ CD是直径,CD⊥AB,(条件)
∴ AM=BM,AC =BC,AD =BD.(结论)
⌒
⌒
⌒
⌒
如图, AB是⊙O的弦(不是直径),作一条平分AB的直径CD, 交AB于点M.
(1)图是轴对称图形吗?如果是,其对称轴是什么?
(2)你能发现图中有哪些等量关系?
说一说你的理由.
是,对称轴是直径CD所在的直线
CD⊥AB,AC=BC,AD=BD
⌒
⌒
⌒
⌒
如图,AB是⊙O的一条弦,作直径CD,使AP=BP.
(1)CD⊥AB吗?为什么?
(2)AC与BC相等吗? AD与BD相等吗?为什么?
⌒
⌒
⌒
⌒
(2)由垂径定理可得AC =BC,AD =BD.
解:(1)连接AO,BO,则AO=BO,
又AE=BE,∴△AOE≌△BOE(SSS),
∴∠AEO=∠BEO=90°,
∴CD⊥AB.
⌒
⌒
⌒
⌒
垂径定理的逆定理
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
用几何语言表述为:
∵ CD是直径,AP=BP,(条件)
∴ AB⊥CD,AC =BC,AD =BD.(结论)
⌒
⌒
⌒
⌒
?
垂径定理的本质是:
知二得三
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分不是直径的弦
(4)这条直线平分不是直径的弦所对的优弧
(5)这条直线平分不是直径的弦所对的劣弧
例题讲解
例1 你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m,你能求出赵州桥主桥拱的半径吗?
A
B
O
C
D
解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
∴ AB=37m,CD=7.23m.
∴ AD= AB=18.5m,OD=OC-CD=R-7.23.
解得R≈27.3(m).
即主桥拱半径约为27.3m.
R2=18.52+(R-7.23)2
∵
A
B
O
C
D
例2 如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD,垂足为F,EF=90m.求这段弯路的半径.
解:连接OC.
设这段弯路的半径为Rm,则OF=(R-90)m.
根据勾股定理,得
解得R=545.
∴这段弯路的半径约为545m.
● O
C
D
E
F
┗
随堂演练
1.下列说法中,不正确的是( ) A.圆既是轴对称图形,又是中心对称图形 B.圆绕着它的圆心旋转任意角度,都会与自身重合 C.圆的对称轴有无数条,对称中心只有一个 D.圆的每一条直径都是它的对称轴
D
2.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B. CB=DB
C.∠ACD=∠ADC D.OM=MB
⌒
⌒
D
3. 如图,⊙O的直径CD=10 cm,AB是⊙O的弦,AM=BM,OM∶OC=3∶5,则AB的长为( )
A.8 cm
cm
C.6 cm
D.2 cm
A
4.如图,AB是⊙O的弦,AB的长为8,P是⊙O上一个动点(不与点A,B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长为___
4
5.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。你认为AC和BD有什么关系?为什么?
理由:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE。
∴ AE-CE=BE-DE
即 AC=BD.
解:AC=BD
O
.
A
C
D
B
E
课堂小结
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论(“知二推三”)
垂直于弦的直径平分弦,
并且平分弦所对的两条弧
两条辅助线:
连半径;作弦心距
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
情境导入
熊宝宝要过生日了!要把蛋糕平均分成四块,你会分吗?
获取新知
问题1 圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
问题2 你是怎么得出结论的?
用折叠的方法
●O
圆的对称性1:
圆是轴对称图形,其对称轴是直径所在的直线
问题3:1.将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
.
O
A
B
180°
所以圆是中心对称图形,对称中心是圆心
问题4:把圆绕圆心旋转任意一个角度呢?
仍与原来的圆重合吗?
·
性质:把圆绕圆心旋转任意一个角度后,仍与原来的圆重合.(圆具有旋转不变性)
圆心角:我们把顶点在圆心的角叫做圆心角.
·
O
B
A
∠AOB为圆心角
圆心角∠AOB所对的弦为AB,所对的弧为AB.
⌒
在同圆中探究
在⊙O中,如果∠AOB= ∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
⌒
·
O
A
B
C
D
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠COD,
那么,AB=CD,弦AB=弦CD
⌒
⌒
在等圆中探究
如图,在等圆中,如果∠AOB=∠CO ′ D,你发现的等量关系是否依然成立?为什么?
·
O
A
B
C
·
O'
D
通过平移和旋转将两个等圆变成同圆
┐
E
·
┐
F
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
在同圆或等圆中
题设
结论
例题讲解
解:
∵
例1 如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
随堂演练
1.如果两个圆心角相等,那么 ( )
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
2.弦长等于半径的弦所对的圆心角等于 .
D
60 °
3.在同圆中,圆心角∠AOB=2∠COD,则AB与CD的关系是( )
⌒ ⌒
A
A. AB=2CD
⌒ ⌒
B. AB>CD
⌒ ⌒
C. AB
D. 不能确定
课堂小结
圆心角
圆心角
相等
弧
相等
弦
相等
弦、弧、圆心角的关系定理
在同圆或等圆中
概念:顶点在圆心的角
应用提醒
①要注意前提条件;
②要灵活转化.
27.1.2 圆的对称性
第2课时 垂径定理
情景导入
问题:你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m,你能求出赵州桥主桥拱的半径吗?
获取新知
如图, AB是⊙O的一条弦,作直径CD,使CD丄AB,垂足为P.
(1)图是轴对称图形吗?如果是,
其对称轴是什么?
(2)你能发现图中有哪些等量关
系?说一说你的理由.
(1)此图是轴对称图形,对称轴是直径CD所在的直线
(2)AP=BP, AC=BC,AD=BD
⌒
⌒
⌒
⌒
已知:在☉O中,CD是直径,AB是弦,AB⊥CD,垂足为P. 求证:AP=BP, AC =BC,AD =BD.
⌒
⌒
⌒
⌒
证明:连接OA、OB、CA、CB,则OA=OB.
即△AOB是等腰三角形.
∵AB⊥CD,
∴AP=BP,∠AOC=∠BOC.
⌒
⌒
AC =BC.
∴AD =BD
⌒
⌒
从而∠AOD=∠BOD.
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
用几何语言表述为:
∵ CD是直径,CD⊥AB,(条件)
∴ AM=BM,AC =BC,AD =BD.(结论)
⌒
⌒
⌒
⌒
如图, AB是⊙O的弦(不是直径),作一条平分AB的直径CD, 交AB于点M.
(1)图是轴对称图形吗?如果是,其对称轴是什么?
(2)你能发现图中有哪些等量关系?
说一说你的理由.
是,对称轴是直径CD所在的直线
CD⊥AB,AC=BC,AD=BD
⌒
⌒
⌒
⌒
如图,AB是⊙O的一条弦,作直径CD,使AP=BP.
(1)CD⊥AB吗?为什么?
(2)AC与BC相等吗? AD与BD相等吗?为什么?
⌒
⌒
⌒
⌒
(2)由垂径定理可得AC =BC,AD =BD.
解:(1)连接AO,BO,则AO=BO,
又AE=BE,∴△AOE≌△BOE(SSS),
∴∠AEO=∠BEO=90°,
∴CD⊥AB.
⌒
⌒
⌒
⌒
垂径定理的逆定理
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
用几何语言表述为:
∵ CD是直径,AP=BP,(条件)
∴ AB⊥CD,AC =BC,AD =BD.(结论)
⌒
⌒
⌒
⌒
?
垂径定理的本质是:
知二得三
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分不是直径的弦
(4)这条直线平分不是直径的弦所对的优弧
(5)这条直线平分不是直径的弦所对的劣弧
例题讲解
例1 你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m,你能求出赵州桥主桥拱的半径吗?
A
B
O
C
D
解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
∴ AB=37m,CD=7.23m.
∴ AD= AB=18.5m,OD=OC-CD=R-7.23.
解得R≈27.3(m).
即主桥拱半径约为27.3m.
R2=18.52+(R-7.23)2
∵
A
B
O
C
D
例2 如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD,垂足为F,EF=90m.求这段弯路的半径.
解:连接OC.
设这段弯路的半径为Rm,则OF=(R-90)m.
根据勾股定理,得
解得R=545.
∴这段弯路的半径约为545m.
● O
C
D
E
F
┗
随堂演练
1.下列说法中,不正确的是( ) A.圆既是轴对称图形,又是中心对称图形 B.圆绕着它的圆心旋转任意角度,都会与自身重合 C.圆的对称轴有无数条,对称中心只有一个 D.圆的每一条直径都是它的对称轴
D
2.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B. CB=DB
C.∠ACD=∠ADC D.OM=MB
⌒
⌒
D
3. 如图,⊙O的直径CD=10 cm,AB是⊙O的弦,AM=BM,OM∶OC=3∶5,则AB的长为( )
A.8 cm
cm
C.6 cm
D.2 cm
A
4.如图,AB是⊙O的弦,AB的长为8,P是⊙O上一个动点(不与点A,B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长为___
4
5.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。你认为AC和BD有什么关系?为什么?
理由:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE。
∴ AE-CE=BE-DE
即 AC=BD.
解:AC=BD
O
.
A
C
D
B
E
课堂小结
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论(“知二推三”)
垂直于弦的直径平分弦,
并且平分弦所对的两条弧
两条辅助线:
连半径;作弦心距
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
