华东师大版九年级数学下册课件:27.1.1 圆的基本元素(18张)
文档属性
| 名称 | 华东师大版九年级数学下册课件:27.1.1 圆的基本元素(18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 23:48:08 | ||
图片预览





文档简介
27.1.1 圆的基本元素
一切平面图形中最美的是圆——毕达哥拉斯
圆象征着圆满和谐
情境导入
圆是常见的图形,生活中的许多物体都给我们以圆的形象(如图).
获取新知
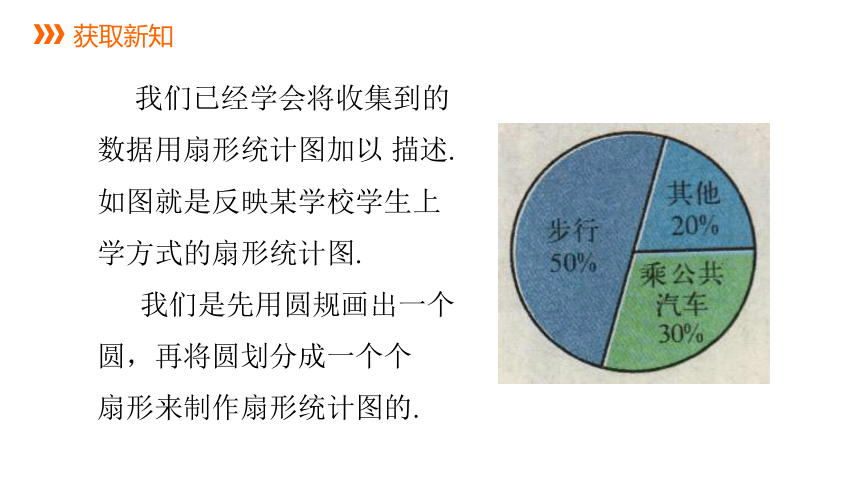
我们已经学会将收集到的
数据用扇形统计图加以 描述.
如图就是反映某学校学生上
学方式的扇形统计图.
我们是先用圆规画出一个
圆,再将圆划分成一个个
扇形来制作扇形统计图的.
·
r
O
A
圆的旋转定义
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.以点O为圆心的圆,记作“⊙O”,读作“圆O”.
有关概念
固定的端点O叫做圆心,线段OA叫做半径,一般用r 表示.
问题 观察画圆的过程,你能说出圆是如何画出来的吗?
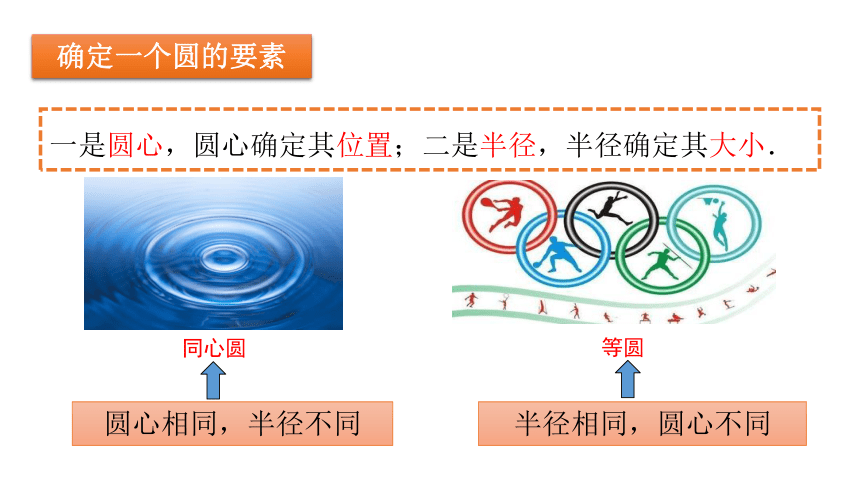
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
同心圆
等圆
半径相同,圆心不同
圆心相同,半径不同
确定一个圆的要素
例1 矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
证明:∵四边形ABCD是矩形,
∴AO=OC,OB=OD.
又∵AC=BD,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
例题讲解
A
B
C
D
O
弦
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
注意
1.弦和直径都是线段;
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
·
C
O
A
B
获取新知
弧:
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
半圆
圆上任意两点间的部分叫做圆弧,简弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
劣弧与优弧
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
·
C
O
A
B
·
C
O
A
B
·
C
O
A
B
圆心O
直径AB
弦AC
优弧ABC,记作
劣弧AC,记作
O′
半径OO′
如图所示 ,已知⊙O上有A,B,C
三个点,以其中两个点为端点的弧
共有________条,弦共有________条.
例2
由弧的概念知以A,B,C中任意两个点为端点的弧有 共6条;由弦的概念知以A,B,C中任意两个点为端点的弦有AB,BC,AC,共3条.
导引:
6
3
例题讲解
等圆:
能够重合的两个圆叫做等圆.
容易看出:
等圆是两个半径相等的圆.
等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
结论:等弧仅仅存在于同圆或者等圆中.
可见这两条弧不可能完全重合
实际上这两条弧弯曲程度不同
“等弧”要区别于“长度相等的弧”
如图,如果AB和CD的拉直长度都是10cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
想一想:长度相等的弧是等弧吗?
A
B
1.下面关于圆的叙述正确的是 ( )
A.圆是一个面
B.圆是一条封闭的曲线
C.圆是由圆心唯一确定的
D.圆是到定点的距离等于或小于定长的点的集合
2.圆内最长的弦的长为30 cm,则圆的半径是 .
随堂演练
B
15cm
3.下列说法中,正确的是 ( )
A.过圆心的线段是直径
B.小于半圆的弧是优弧
C.弦是直径
D.半圆是弧
D
4.如图.
(1)请写出以点A为端点的优弧及劣弧;
(2)请写出以点A为端点的弦及直径.
弦AF,AB,AC.其中弦AB又是直径.
劣弧:
优弧:
AF,
(
AD,
(
AC,
(
AE.
(
AFE,
(
AFC,
(
ADE,
(
ADC.
(
(3)请任选一条弦,写出这条弦所对的弧.
答案不唯一,如:弦AF,它所对的弧是 .
AF
(
A
B
C
E
F
D
O
课堂小结
圆
定义
旋转定义
要画一个确定的圆,关键是
确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
圆心角
顶点在圆心,并且两边都和圆周相交的角
一切平面图形中最美的是圆——毕达哥拉斯
圆象征着圆满和谐
情境导入
圆是常见的图形,生活中的许多物体都给我们以圆的形象(如图).
获取新知
我们已经学会将收集到的
数据用扇形统计图加以 描述.
如图就是反映某学校学生上
学方式的扇形统计图.
我们是先用圆规画出一个
圆,再将圆划分成一个个
扇形来制作扇形统计图的.
·
r
O
A
圆的旋转定义
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.以点O为圆心的圆,记作“⊙O”,读作“圆O”.
有关概念
固定的端点O叫做圆心,线段OA叫做半径,一般用r 表示.
问题 观察画圆的过程,你能说出圆是如何画出来的吗?
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
同心圆
等圆
半径相同,圆心不同
圆心相同,半径不同
确定一个圆的要素
例1 矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
证明:∵四边形ABCD是矩形,
∴AO=OC,OB=OD.
又∵AC=BD,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
例题讲解
A
B
C
D
O
弦
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
注意
1.弦和直径都是线段;
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
·
C
O
A
B
获取新知
弧:
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
半圆
圆上任意两点间的部分叫做圆弧,简弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
劣弧与优弧
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
·
C
O
A
B
·
C
O
A
B
·
C
O
A
B
圆心O
直径AB
弦AC
优弧ABC,记作
劣弧AC,记作
O′
半径OO′
如图所示 ,已知⊙O上有A,B,C
三个点,以其中两个点为端点的弧
共有________条,弦共有________条.
例2
由弧的概念知以A,B,C中任意两个点为端点的弧有 共6条;由弦的概念知以A,B,C中任意两个点为端点的弦有AB,BC,AC,共3条.
导引:
6
3
例题讲解
等圆:
能够重合的两个圆叫做等圆.
容易看出:
等圆是两个半径相等的圆.
等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
结论:等弧仅仅存在于同圆或者等圆中.
可见这两条弧不可能完全重合
实际上这两条弧弯曲程度不同
“等弧”要区别于“长度相等的弧”
如图,如果AB和CD的拉直长度都是10cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
想一想:长度相等的弧是等弧吗?
A
B
1.下面关于圆的叙述正确的是 ( )
A.圆是一个面
B.圆是一条封闭的曲线
C.圆是由圆心唯一确定的
D.圆是到定点的距离等于或小于定长的点的集合
2.圆内最长的弦的长为30 cm,则圆的半径是 .
随堂演练
B
15cm
3.下列说法中,正确的是 ( )
A.过圆心的线段是直径
B.小于半圆的弧是优弧
C.弦是直径
D.半圆是弧
D
4.如图.
(1)请写出以点A为端点的优弧及劣弧;
(2)请写出以点A为端点的弦及直径.
弦AF,AB,AC.其中弦AB又是直径.
劣弧:
优弧:
AF,
(
AD,
(
AC,
(
AE.
(
AFE,
(
AFC,
(
ADE,
(
ADC.
(
(3)请任选一条弦,写出这条弦所对的弧.
答案不唯一,如:弦AF,它所对的弧是 .
AF
(
A
B
C
E
F
D
O
课堂小结
圆
定义
旋转定义
要画一个确定的圆,关键是
确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
圆心角
顶点在圆心,并且两边都和圆周相交的角
