青岛版数学八年级上册5.4 平行线的性质定理和判定定理 课件(14张)
文档属性
| 名称 | 青岛版数学八年级上册5.4 平行线的性质定理和判定定理 课件(14张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 219.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 00:00:00 | ||
图片预览






文档简介
5.4平行线的性质定理和判定定理
青岛版义务教育教科书
八年级数学上册
请问:猴子为什么不喜欢平行线?
因为它永远没有相交(香蕉)。
5.4 平行线的性质定理和判定定理
学习目标
1、会区分并证明平行线的性质和判定定理。
2、了解互逆命题、互逆定理的概念。
3、熟悉证明的步骤和格式,感受几何证明的
严谨性。
1、两条直线被第三条直线所截,可以得到几对对顶角?
不共顶点的角的位置关系有几种?
2、曾经探索得到的平行线的性质有哪些?平行线的判定方法有哪些?
平行线的性质定理1:
两条平行线被第三条直线所截,同位角相等。
平行线的性质定理2:
两条平行线被第三条直线所截,内错角相等。
平行线的性质定理3:
两条平行线被第三条直线所截,同旁内角互补。
平行线的判定定理:
两条直线被第三条直线所截,同位角相等,两直线平行。
平行线的判定定理1:
两条直线被第三条直线所截,内错角相等,两直线平行。
平行线的判定定理2:
两条直线被第三条直线所截,同旁内角互补,两直线平行。
温故知新
平行线的判定定理
两条直线被第三条直线所截,如果同位角相等,
那么两直线平行。同位角相等,两直线平行。
基本事实
平行线的性质定理1:
两条平行线,同位角相等。
注:性质定理1,现阶段不用证明,直接作为结论应用于各种证明问题中。
两直线平行,内错角相等。
指出定理的条件和结论并画出图形,结合图形写出已知、求证.
活动一:
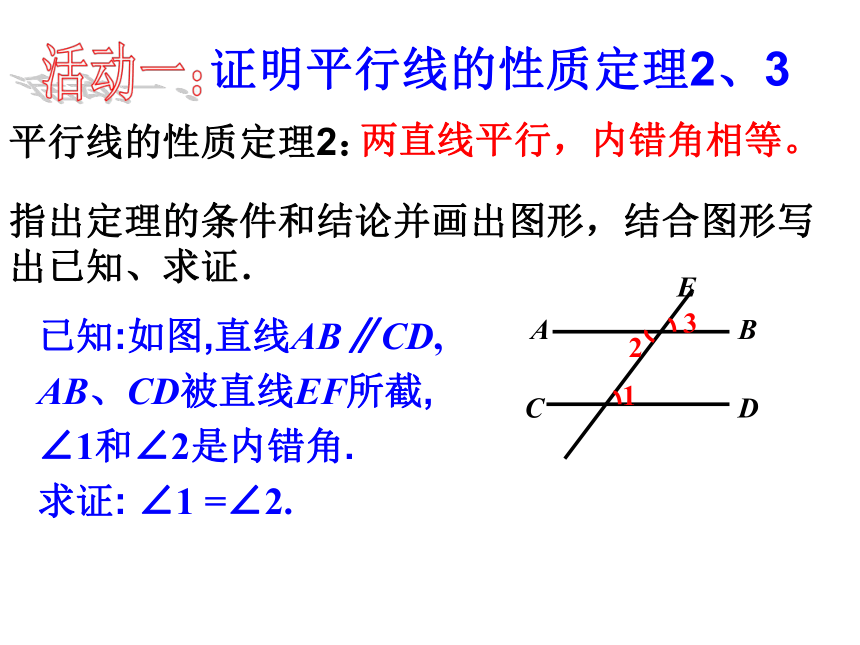
平行线的性质定理2:
已知:如图,直线AB∥CD,
AB、CD被直线EF所截,
∠1和∠2是内错角.
求证: ∠1 =∠2.
A
B
D
C
E
3
2
1
证明平行线的性质定理2、3
两直线平行,同旁内角互补。
平行线的性质定理3:
已知:如图,直线AB∥CD, AB、CD被直线EF所截,∠1和∠2是同旁内角.
求证: ∠1 +∠2 =180°.
A
B
D
C
E
3
2
1
平行线的判定定理1:
内错角相等,两直线平行。
活动二:
证明平行线的判定定理1、2
已知:如图,∠1和∠2是直线
a,b被直线c截出的内错角,
且∠1=∠2.
求证:a∥b.
a
b
c
1
3
2
平行线的判定定理2:
同旁内角互补,两直
线平行。
已知:如图,直线a、b被直线
c所截, ∠1 +∠2 =180°.
求证: a∥b .
a
b
c
1
3
2
每组单号
完成本题
每组双号
完成本题
这里的结论,以后
可以直接运用.
活动三:
探究互逆命题、互逆定理
自主学习
自学课本167--168页“交流与发现”的内容,
完成以下问题:
(1)什么叫互逆命题?二者的关系是什么?
(2)如何说出一个命题的逆命题?
(3)一个命题的逆命题一定正确吗?
(4)所有的定理都有逆定理吗?举例说明。
自学完成后,小组交流
把一个命题的条件和结论交换后,就构成了一个新的命题.如果把原来的命题叫做原命题,那么这个新的命题就叫做原命题的逆命题.
一个命题是真命题,它的逆命题不一定是真命题
互逆定理
内错角相等,两直线平行.
两直线平行,内错角相等.
如果两个角是直角, 那么这两个角相等.
如果两个三角形全等,那么它们的对应边相等.
结论
条件
我来说
如果a,b互为相反数,那么a+b=0.
如果a+b=0,那么a,b互为相反数.
如果两个角相等, 那么这两个角是直角.
如果两个三角形对应边相等,那么这两个三角形全等.
注:先确定命题的条件和结论,
然后再确定逆命题。
1、 说出下列命题的逆命题,并指出是真命题还是假命题?
(1)两条平行线被第三条直线所截,同旁内角互补。
(2)对顶角相等。
(3)两条平行线被第三条直线所截,内错角相等。
达标测试
2、已知:如图,直线c、d与直线a、b分别相交,∠ 1 =∠ 2, ∠3=55 °.
求:∠4的度数.
a
d
c
b
1
2
3
4
5
6
谈收获
青岛版义务教育教科书
八年级数学上册
请问:猴子为什么不喜欢平行线?
因为它永远没有相交(香蕉)。
5.4 平行线的性质定理和判定定理
学习目标
1、会区分并证明平行线的性质和判定定理。
2、了解互逆命题、互逆定理的概念。
3、熟悉证明的步骤和格式,感受几何证明的
严谨性。
1、两条直线被第三条直线所截,可以得到几对对顶角?
不共顶点的角的位置关系有几种?
2、曾经探索得到的平行线的性质有哪些?平行线的判定方法有哪些?
平行线的性质定理1:
两条平行线被第三条直线所截,同位角相等。
平行线的性质定理2:
两条平行线被第三条直线所截,内错角相等。
平行线的性质定理3:
两条平行线被第三条直线所截,同旁内角互补。
平行线的判定定理:
两条直线被第三条直线所截,同位角相等,两直线平行。
平行线的判定定理1:
两条直线被第三条直线所截,内错角相等,两直线平行。
平行线的判定定理2:
两条直线被第三条直线所截,同旁内角互补,两直线平行。
温故知新
平行线的判定定理
两条直线被第三条直线所截,如果同位角相等,
那么两直线平行。同位角相等,两直线平行。
基本事实
平行线的性质定理1:
两条平行线,同位角相等。
注:性质定理1,现阶段不用证明,直接作为结论应用于各种证明问题中。
两直线平行,内错角相等。
指出定理的条件和结论并画出图形,结合图形写出已知、求证.
活动一:
平行线的性质定理2:
已知:如图,直线AB∥CD,
AB、CD被直线EF所截,
∠1和∠2是内错角.
求证: ∠1 =∠2.
A
B
D
C
E
3
2
1
证明平行线的性质定理2、3
两直线平行,同旁内角互补。
平行线的性质定理3:
已知:如图,直线AB∥CD, AB、CD被直线EF所截,∠1和∠2是同旁内角.
求证: ∠1 +∠2 =180°.
A
B
D
C
E
3
2
1
平行线的判定定理1:
内错角相等,两直线平行。
活动二:
证明平行线的判定定理1、2
已知:如图,∠1和∠2是直线
a,b被直线c截出的内错角,
且∠1=∠2.
求证:a∥b.
a
b
c
1
3
2
平行线的判定定理2:
同旁内角互补,两直
线平行。
已知:如图,直线a、b被直线
c所截, ∠1 +∠2 =180°.
求证: a∥b .
a
b
c
1
3
2
每组单号
完成本题
每组双号
完成本题
这里的结论,以后
可以直接运用.
活动三:
探究互逆命题、互逆定理
自主学习
自学课本167--168页“交流与发现”的内容,
完成以下问题:
(1)什么叫互逆命题?二者的关系是什么?
(2)如何说出一个命题的逆命题?
(3)一个命题的逆命题一定正确吗?
(4)所有的定理都有逆定理吗?举例说明。
自学完成后,小组交流
把一个命题的条件和结论交换后,就构成了一个新的命题.如果把原来的命题叫做原命题,那么这个新的命题就叫做原命题的逆命题.
一个命题是真命题,它的逆命题不一定是真命题
互逆定理
内错角相等,两直线平行.
两直线平行,内错角相等.
如果两个角是直角, 那么这两个角相等.
如果两个三角形全等,那么它们的对应边相等.
结论
条件
我来说
如果a,b互为相反数,那么a+b=0.
如果a+b=0,那么a,b互为相反数.
如果两个角相等, 那么这两个角是直角.
如果两个三角形对应边相等,那么这两个三角形全等.
注:先确定命题的条件和结论,
然后再确定逆命题。
1、 说出下列命题的逆命题,并指出是真命题还是假命题?
(1)两条平行线被第三条直线所截,同旁内角互补。
(2)对顶角相等。
(3)两条平行线被第三条直线所截,内错角相等。
达标测试
2、已知:如图,直线c、d与直线a、b分别相交,∠ 1 =∠ 2, ∠3=55 °.
求:∠4的度数.
a
d
c
b
1
2
3
4
5
6
谈收获
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
