青岛版八年级数学上册2.6.1 等腰三角形的性质教学课件(20张)
文档属性
| 名称 | 青岛版八年级数学上册2.6.1 等腰三角形的性质教学课件(20张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 61.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 23:54:32 | ||
图片预览






文档简介
温馨提示
请准备好课本、导学案、练习本、典题本、双色笔、作图工具、还有饱满的精神状态!
轴对称图形
一.什么是轴对称图形?
一个图形的一部分,
以某条直线为对称轴,
经过轴对称能与图形的另一部分重合,这样的图形叫做轴对称图形。
二.我们学习过的基本的几何图形中,轴对称图形有哪些?
1.对称轴是什么?
2.对称轴有什么性质?
对称轴:线段的垂直平分线
线段 :
A
B
.P
垂直平分线性质:
线段垂直平分线上的点到线段两端的距离相等。
到线段两端点距离相等的点在线段的垂直平分线上。
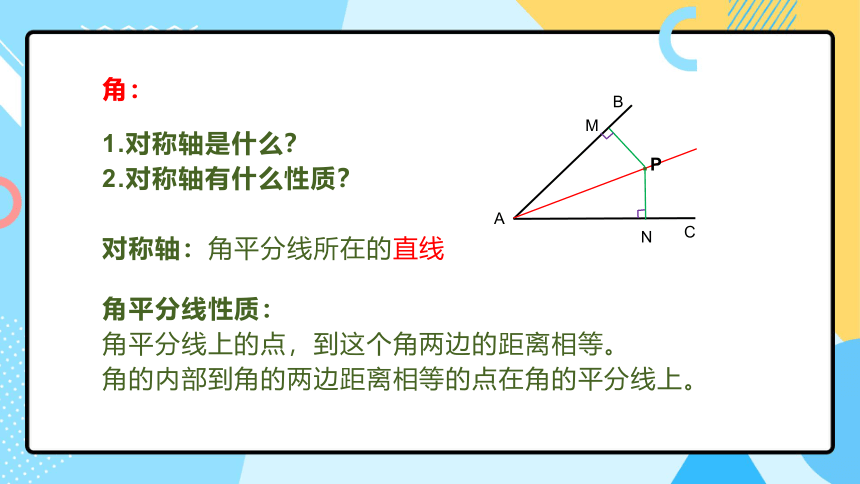
角:
1.对称轴是什么?
2.对称轴有什么性质?
对称轴:角平分线所在的直线
A
C
B
.P
M
N
角平分线性质:
角平分线上的点,到这个角两边的距离相等。
角的内部到角的两边距离相等的点在角的平分线上。
思考:任意画一个三角形,它是轴对称图形吗?
如果是等腰三角形呢?它是不是轴对称图形?
A
C
B
A
B
C
2.6.1 等腰三角形的性质
学习目标
1.折叠等腰三角形纸片,探究其边角关系,说出等腰三角形的性质;
2.借助等腰三角形性质解决角的度数和线段长度问题;
3.已知底边和底边上的高,会用尺规作图作出等腰三角形.
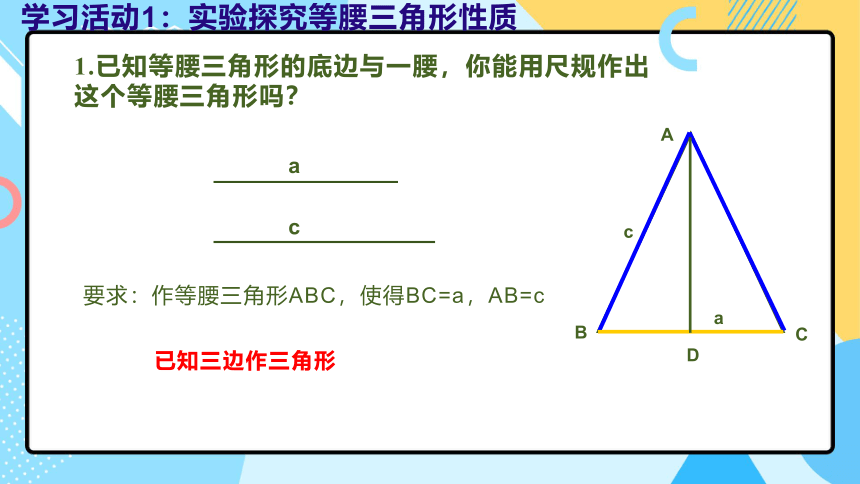
1.已知等腰三角形的底边与一腰,你能用尺规作出
这个等腰三角形吗?
学习活动1:实验探究等腰三角形性质
A
B
C
D
a
要求:作等腰三角形ABC,使得BC=a,AB=c
c
a
c
已知三边作三角形
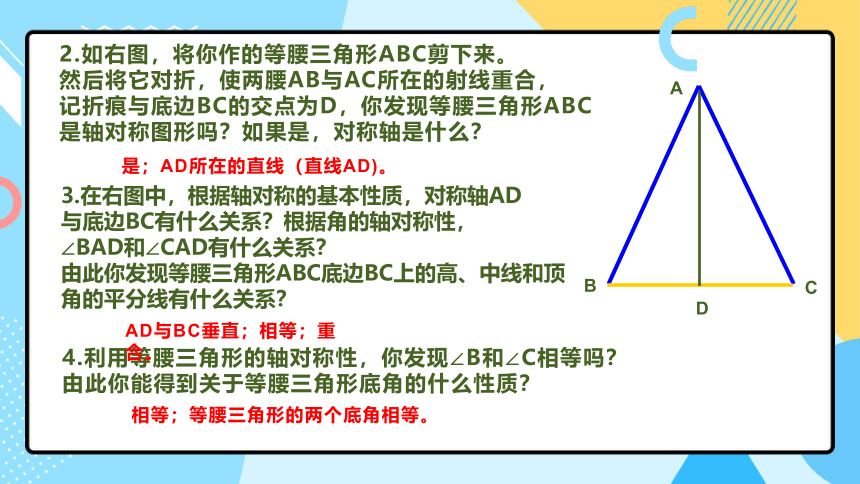
2.如右图,将你作的等腰三角形ABC剪下来。
然后将它对折,使两腰AB与AC所在的射线重合,
记折痕与底边BC的交点为D,你发现等腰三角形ABC
是轴对称图形吗?如果是,对称轴是什么?
A
B
C
D
3.在右图中,根据轴对称的基本性质,对称轴AD
与底边BC有什么关系?根据角的轴对称性,
∠BAD和∠CAD有什么关系?
由此你发现等腰三角形ABC底边BC上的高、中线和顶角的平分线有什么关系?
4.利用等腰三角形的轴对称性,你发现∠B和∠C相等吗?
由此你能得到关于等腰三角形底角的什么性质?
是;AD所在的直线(直线AD)。
相等;等腰三角形的两个底角相等。
AD与BC垂直;相等;重合。
5.你能总结一下等腰三角形的性质吗?
(1)等腰三角形是轴对称图形,等腰三角形的对称轴是底边的垂直平分线。(对称性)
(2)等腰三角形的顶角平分线,底边上的高、底边上的中线重合。(三线合一)
(3)等腰三角形的两个底角相等。(等边对等角)
A
B
C
D
1
2
1.等腰三角形的顶角的平分线,既是底边上的中线,又是底边上的高。
符号语言:∵AB=AC ∠BAD=∠CAD(已知)
∴BD=DC AD⊥BC(等腰三角形三线合一)
2.等腰三角形的底边上中线,既是底边上的高,又是顶角平分线。
符号语言: ∵AB=AC BD=DC (已知)
∴AD⊥BC ∠BAD=∠CAD (等腰三角形三线合一)
3.等腰三角形的底边上的高,既是底边上的中线,又是顶角平分线。
符号语言: ∵AB=AC AD⊥BC (已知)
∴BD=DC ∠BAD=∠CAD (等腰三角形三线合一)
三线合一符号语言运用:
符号语言:
在?ABC中,
∵ AB=AC( 已知)
∴ ∠B=∠C (等边对等角)
等腰三角形的性质:等腰三角形的两个底角相等
学习活动2:等腰三角形性质的应用
已知:如图,房屋的顶角∠BAC=100 ?, 过屋顶A的立柱AD ? BC , 屋椽AB=AC.
求顶架上∠B、∠C、∠BAD、∠CAD的度数.
A
B
D
C
解:在?ABC中
∵AB=AC,
∴∠B=∠C(等边对等角)
∴∠B=∠C= 1/2 (180°-∠A)
=40°(三角形内角和定理)
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD(等腰三角形顶角的平分线
与底边上的高互相重合).
∴∠BAD=∠CAD=50°
1.等腰三角形一个顶角为70°,其它两个角为_________.
55°,55°
3.如图,在△ABC中,AB=AC,AE是BC边上的高,
BD为AC边上的高,已知∠EAD=20°,
则∠ABD的度数是( )。
A.20° B.40° C.50° D.70°
C
2.等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
19cm
学习活动3:作等腰三角形
已知:线段a,h.
求作:?ABC,使AC=BC,且AB=a,高CD=h.
h
a
C
A
D
B
h
a
目标图示
作法:
1.作线段AB=a;
2.作线段AB的垂直平分线EF,交AB于点D;
3.在EF上截取DC=h;
4.连接AC,BC.
?ABC就是所求作的等腰三角形.
尺规作几何图形的注意问题:
1.画出目标图形,标注好已知条件;(作什么)
2.分析作图方法;(怎么作)
3.明确作图依据;(为什么这么作)
4.保留作图痕迹;
5.写出规范作法,下好结论。
等腰三角形的性质
1.等腰三角形是轴对称图形,等腰三角形的对称轴是底边的垂直平分线。(对称性)
2.等腰三角形的顶角平分线,底边上的高、底边上的中线重合。(三线合一)
3.等腰三角形的两个底角相等。(等边对等角)
等腰三角形性质的应用
研究边角关系、求角度数、求边长、周长、作等腰三角形……
落 实 巩 固
1.下列图形中,不是轴对称图形的是( )
A. 等腰三角形 B. 线段
C. 钝角 D. 直角三角形
2.等腰三角形的底角是顶角的2倍,则底角度数为( )
A. 36° B. 32° C. 64° D. 72°
3.等腰三角形的一个角是80°,则它的另外两个角
是_________.
4.等腰三角形的一边为5,另一边为3,则它的周长为_________.
D
D
50°、50°或80°、20°
13或11
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
请准备好课本、导学案、练习本、典题本、双色笔、作图工具、还有饱满的精神状态!
轴对称图形
一.什么是轴对称图形?
一个图形的一部分,
以某条直线为对称轴,
经过轴对称能与图形的另一部分重合,这样的图形叫做轴对称图形。
二.我们学习过的基本的几何图形中,轴对称图形有哪些?
1.对称轴是什么?
2.对称轴有什么性质?
对称轴:线段的垂直平分线
线段 :
A
B
.P
垂直平分线性质:
线段垂直平分线上的点到线段两端的距离相等。
到线段两端点距离相等的点在线段的垂直平分线上。
角:
1.对称轴是什么?
2.对称轴有什么性质?
对称轴:角平分线所在的直线
A
C
B
.P
M
N
角平分线性质:
角平分线上的点,到这个角两边的距离相等。
角的内部到角的两边距离相等的点在角的平分线上。
思考:任意画一个三角形,它是轴对称图形吗?
如果是等腰三角形呢?它是不是轴对称图形?
A
C
B
A
B
C
2.6.1 等腰三角形的性质
学习目标
1.折叠等腰三角形纸片,探究其边角关系,说出等腰三角形的性质;
2.借助等腰三角形性质解决角的度数和线段长度问题;
3.已知底边和底边上的高,会用尺规作图作出等腰三角形.
1.已知等腰三角形的底边与一腰,你能用尺规作出
这个等腰三角形吗?
学习活动1:实验探究等腰三角形性质
A
B
C
D
a
要求:作等腰三角形ABC,使得BC=a,AB=c
c
a
c
已知三边作三角形
2.如右图,将你作的等腰三角形ABC剪下来。
然后将它对折,使两腰AB与AC所在的射线重合,
记折痕与底边BC的交点为D,你发现等腰三角形ABC
是轴对称图形吗?如果是,对称轴是什么?
A
B
C
D
3.在右图中,根据轴对称的基本性质,对称轴AD
与底边BC有什么关系?根据角的轴对称性,
∠BAD和∠CAD有什么关系?
由此你发现等腰三角形ABC底边BC上的高、中线和顶角的平分线有什么关系?
4.利用等腰三角形的轴对称性,你发现∠B和∠C相等吗?
由此你能得到关于等腰三角形底角的什么性质?
是;AD所在的直线(直线AD)。
相等;等腰三角形的两个底角相等。
AD与BC垂直;相等;重合。
5.你能总结一下等腰三角形的性质吗?
(1)等腰三角形是轴对称图形,等腰三角形的对称轴是底边的垂直平分线。(对称性)
(2)等腰三角形的顶角平分线,底边上的高、底边上的中线重合。(三线合一)
(3)等腰三角形的两个底角相等。(等边对等角)
A
B
C
D
1
2
1.等腰三角形的顶角的平分线,既是底边上的中线,又是底边上的高。
符号语言:∵AB=AC ∠BAD=∠CAD(已知)
∴BD=DC AD⊥BC(等腰三角形三线合一)
2.等腰三角形的底边上中线,既是底边上的高,又是顶角平分线。
符号语言: ∵AB=AC BD=DC (已知)
∴AD⊥BC ∠BAD=∠CAD (等腰三角形三线合一)
3.等腰三角形的底边上的高,既是底边上的中线,又是顶角平分线。
符号语言: ∵AB=AC AD⊥BC (已知)
∴BD=DC ∠BAD=∠CAD (等腰三角形三线合一)
三线合一符号语言运用:
符号语言:
在?ABC中,
∵ AB=AC( 已知)
∴ ∠B=∠C (等边对等角)
等腰三角形的性质:等腰三角形的两个底角相等
学习活动2:等腰三角形性质的应用
已知:如图,房屋的顶角∠BAC=100 ?, 过屋顶A的立柱AD ? BC , 屋椽AB=AC.
求顶架上∠B、∠C、∠BAD、∠CAD的度数.
A
B
D
C
解:在?ABC中
∵AB=AC,
∴∠B=∠C(等边对等角)
∴∠B=∠C= 1/2 (180°-∠A)
=40°(三角形内角和定理)
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD(等腰三角形顶角的平分线
与底边上的高互相重合).
∴∠BAD=∠CAD=50°
1.等腰三角形一个顶角为70°,其它两个角为_________.
55°,55°
3.如图,在△ABC中,AB=AC,AE是BC边上的高,
BD为AC边上的高,已知∠EAD=20°,
则∠ABD的度数是( )。
A.20° B.40° C.50° D.70°
C
2.等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
19cm
学习活动3:作等腰三角形
已知:线段a,h.
求作:?ABC,使AC=BC,且AB=a,高CD=h.
h
a
C
A
D
B
h
a
目标图示
作法:
1.作线段AB=a;
2.作线段AB的垂直平分线EF,交AB于点D;
3.在EF上截取DC=h;
4.连接AC,BC.
?ABC就是所求作的等腰三角形.
尺规作几何图形的注意问题:
1.画出目标图形,标注好已知条件;(作什么)
2.分析作图方法;(怎么作)
3.明确作图依据;(为什么这么作)
4.保留作图痕迹;
5.写出规范作法,下好结论。
等腰三角形的性质
1.等腰三角形是轴对称图形,等腰三角形的对称轴是底边的垂直平分线。(对称性)
2.等腰三角形的顶角平分线,底边上的高、底边上的中线重合。(三线合一)
3.等腰三角形的两个底角相等。(等边对等角)
等腰三角形性质的应用
研究边角关系、求角度数、求边长、周长、作等腰三角形……
落 实 巩 固
1.下列图形中,不是轴对称图形的是( )
A. 等腰三角形 B. 线段
C. 钝角 D. 直角三角形
2.等腰三角形的底角是顶角的2倍,则底角度数为( )
A. 36° B. 32° C. 64° D. 72°
3.等腰三角形的一个角是80°,则它的另外两个角
是_________.
4.等腰三角形的一边为5,另一边为3,则它的周长为_________.
D
D
50°、50°或80°、20°
13或11
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
——华罗庚
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
