人教版八年级数学上册11.3.1 多边形课件(22张)
文档属性
| 名称 | 人教版八年级数学上册11.3.1 多边形课件(22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 922.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:53 | ||
图片预览




文档简介
人教版八年级数学上册 11.3 多边形及其内角和
11.3.1 多边形
了解多边形及有关概念,理解正多边形及其有关概念;
区别凸多边形与凹多边形。
学习目标
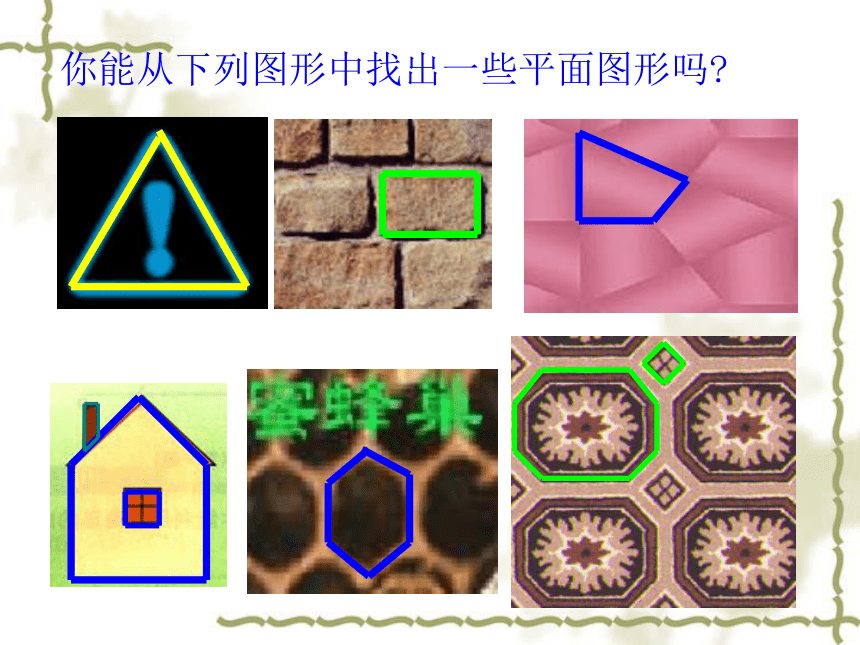
你能从下列图形中找出一些平面图形吗?
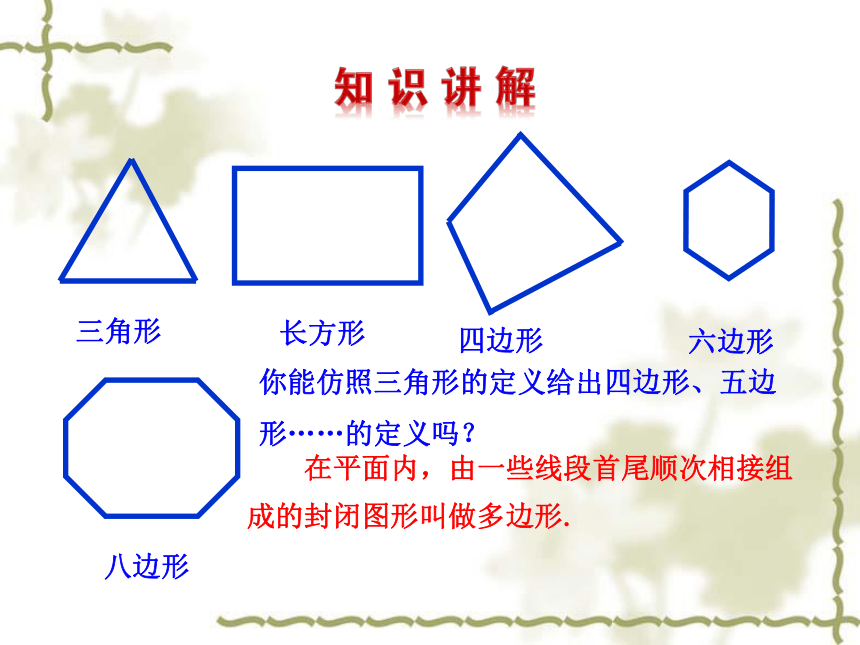
三角形
长方形
六边形
四边形
八边形
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
你能仿照三角形的定义给出四边形、五边形……的定义吗?
多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形。
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形。
注意:n所代表的数字必须是汉字中的数字,如三角形,六边形,十边形等等,但当问题问这个多边形有多少条边时,我们可以用阿拉伯数字说明这个n边形有3条边,4条边等。
在多边形的概念中,要分清以下几个方面
(1)在同一平面内;
(2)若干线段不在同一直线上;
(3)首尾顺次相结;
(4)所形成的封闭图形
多边形概念的重要提示:
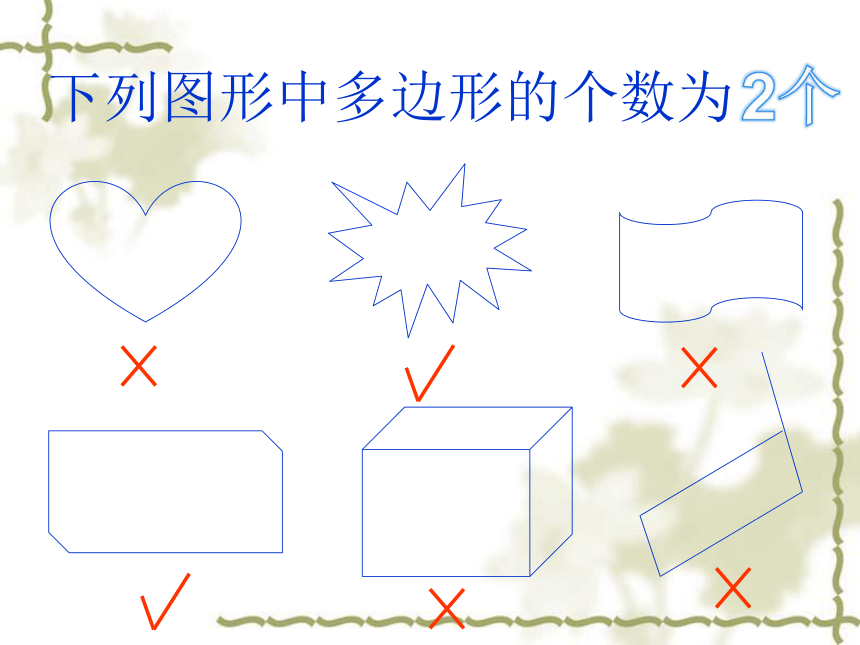
下列图形中多边形的个数为
2个
A
B
C
D
E
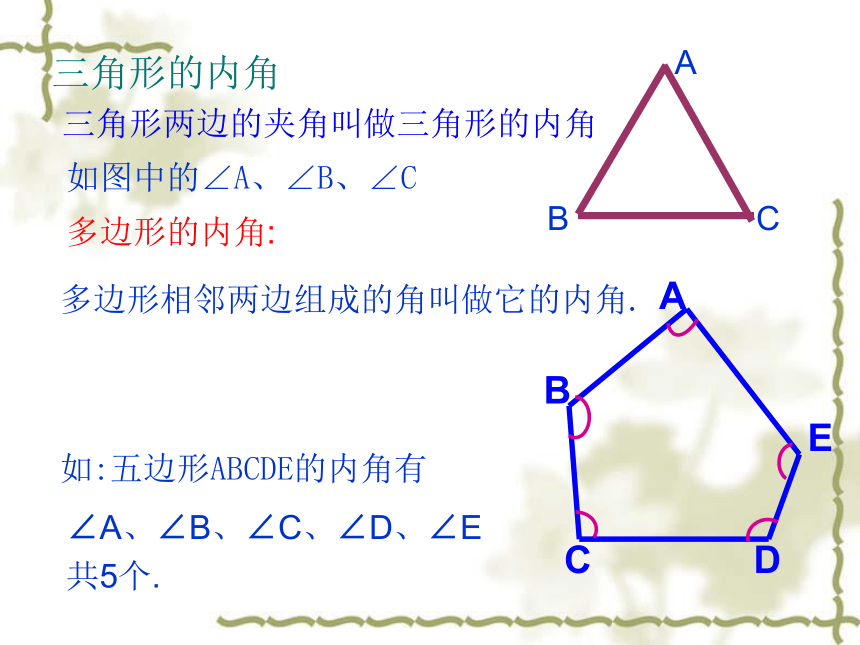
多边形相邻两边组成的角叫做它的内角.
如:五边形ABCDE的内角有
A
B
C
三角形两边的夹角叫做三角形的内角
如图中的∠A、∠B、∠C
多边形的内角:
三角形的内角
∠A、∠B、∠C、∠D、∠E
共5个.
A
B
C
D
E
2
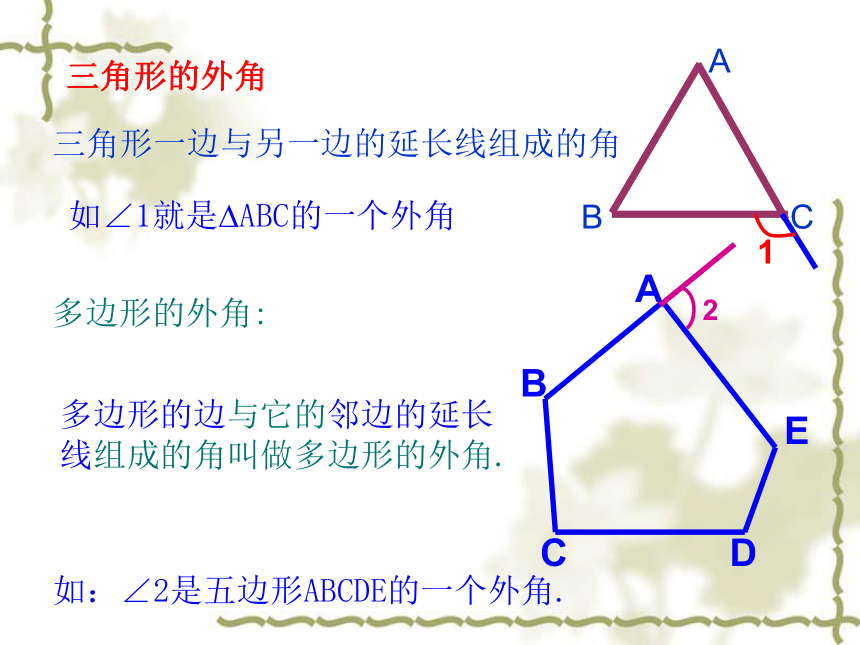
三角形的外角
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
如:∠2是五边形ABCDE的一个外角.
A
B
C
1
三角形一边与另一边的延长线组成的角
如∠1就是?ABC的一个外角
多边形的外角:
A
B
C
D
E
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
如图中的线段AC、AD、BE等
三角形是最简单的多边形,研究可借助对角线将其分为若干个三角形
多边形的对角线:
画出多边形中从一个顶点出发的对角线,写出它的条数.
0
1
2
3
5
从n边形的一个顶点出发能画出多少条对角线?
你能写出每个图形中对角线的总条数吗?如果不能,请画出所有对角线.
0
2
5
9
你能告诉我二十边形的对角线的总条数吗?五十边形呢?一百边形呢?n边形呢?
太难画了!
探索
边数
3
4
5
6
7
…
n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数
…
总的对角线条数
…
0
1
0
1
2
2
2
3
5
3
4
9
4
5
14
n-3
n-2
n(n-3)
2
n边形对角线条数:
n(n-3)
2
A
B
C
D
A
B
C
D
图1
图2
图2中,多边形ABCD不在CD所在直线的同侧,就不是凸多边形,叫凹多边形.
在图1中,画出任意一边所在的直线,整个多边形都在直线的同侧,这样的多边形叫做凸多边形.
没有特别说明,我们研究的多边形都是指凸多边形.
多边形的分类
观察图中的多边形,他们的边、角有什么特点?
在平面内,各个角都相等、各条边都相等的多边形叫做正多边形。
正三角形
正方形
正五边形
正六边形
正八边形
正多边形的概念
当n>3时,必须同时满足以下两个条件:
(1)是各边相等,
(2)是各角相等.
两者缺一不可
如长方形各角相等,但各边不一定相等,菱形各边相等,但各角不一定相等,所以它们都不是正多边形。
判断一个n边形是正n边形的条件是:
菱形
矩形
正三角形
正方形
5、多边形分为___________和____________两类.
4、正多边形的_____相等,____相等.
3、从五边形的一个顶点出发可以画_____条对角线,它们将五边形分成______个三角形.
2、四边形有_____条对角线。五边形有______条对角线。四边形的一条对角线将它分成______个三角形.
1、n边形有______个顶点,_____边,有_____个角,有________个不共顶点外角.
n
n
n
n
2
5
2
3
2
边
角
凸多边形
凹多边形
课堂练习
1.下列不是凸多边形的是( )
A B C D
2. 下列图形中∠1是外角的是( )
A B C D
3.下列说法正确的是( )
A.一个多边形外角的个数与边数相同.
B. 一个多边形外角的个数是边数的二倍.
C.每个角都相等的多边形是正多边形.
D.每条边都相等的多边形是正多边形.
一试身手
C
1
1
1
1
D
B
练一练:
1、下列叙述正确的是( )
A、每条边都相等的多边形是正多边形。
B、如果画出多边形某一条边所在的直线, 这个多边形都在这条直线的同一侧,那么
它一定是凸多边形。
C、每个角都相等的多边形叫正多边形。
D、每条边、每个角都相等的多边形叫正多边形。
2、小学学过的下列图形中不可能是正多边形的是( )
A、三角形 B、正方形 C、四边形 D、梯形
D
D
把一个五边形锯去一个内角后得到是什么图形?请画图说明
①
②
③
解:五边形锯去一个内角后得到的图形可能是六边形,如图①;五边形,如图②;四边形,如图③
拓展题
将一个多边形(边数大于3)截去一个角,不同的截法会出现不同的结果:
(1)边数减1;(2)边数不变;(3)边数加1
小结
1、多边形的定义
在平面内,由一些线段首尾顺次相接组成的图形
2、多边形的内角
多边形相邻两边组成的角
3、多边形的外角
多边形的一边与它相邻边的反向延长线组成的角
4、多边形的对角线
连接多边形不相邻的两个顶点的线段
5、正多边形
各个角相等,各条边都相等的多边形
结论
n边形从一个顶点出发的对角线有(n-3)条,
把n边形分成(n - 2)个三角形(n≥3)
n边形共有对角线 条(n≥3)
11.3.1 多边形
了解多边形及有关概念,理解正多边形及其有关概念;
区别凸多边形与凹多边形。
学习目标
你能从下列图形中找出一些平面图形吗?
三角形
长方形
六边形
四边形
八边形
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
你能仿照三角形的定义给出四边形、五边形……的定义吗?
多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形。
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形。
注意:n所代表的数字必须是汉字中的数字,如三角形,六边形,十边形等等,但当问题问这个多边形有多少条边时,我们可以用阿拉伯数字说明这个n边形有3条边,4条边等。
在多边形的概念中,要分清以下几个方面
(1)在同一平面内;
(2)若干线段不在同一直线上;
(3)首尾顺次相结;
(4)所形成的封闭图形
多边形概念的重要提示:
下列图形中多边形的个数为
2个
A
B
C
D
E
多边形相邻两边组成的角叫做它的内角.
如:五边形ABCDE的内角有
A
B
C
三角形两边的夹角叫做三角形的内角
如图中的∠A、∠B、∠C
多边形的内角:
三角形的内角
∠A、∠B、∠C、∠D、∠E
共5个.
A
B
C
D
E
2
三角形的外角
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
如:∠2是五边形ABCDE的一个外角.
A
B
C
1
三角形一边与另一边的延长线组成的角
如∠1就是?ABC的一个外角
多边形的外角:
A
B
C
D
E
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
如图中的线段AC、AD、BE等
三角形是最简单的多边形,研究可借助对角线将其分为若干个三角形
多边形的对角线:
画出多边形中从一个顶点出发的对角线,写出它的条数.
0
1
2
3
5
从n边形的一个顶点出发能画出多少条对角线?
你能写出每个图形中对角线的总条数吗?如果不能,请画出所有对角线.
0
2
5
9
你能告诉我二十边形的对角线的总条数吗?五十边形呢?一百边形呢?n边形呢?
太难画了!
探索
边数
3
4
5
6
7
…
n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数
…
总的对角线条数
…
0
1
0
1
2
2
2
3
5
3
4
9
4
5
14
n-3
n-2
n(n-3)
2
n边形对角线条数:
n(n-3)
2
A
B
C
D
A
B
C
D
图1
图2
图2中,多边形ABCD不在CD所在直线的同侧,就不是凸多边形,叫凹多边形.
在图1中,画出任意一边所在的直线,整个多边形都在直线的同侧,这样的多边形叫做凸多边形.
没有特别说明,我们研究的多边形都是指凸多边形.
多边形的分类
观察图中的多边形,他们的边、角有什么特点?
在平面内,各个角都相等、各条边都相等的多边形叫做正多边形。
正三角形
正方形
正五边形
正六边形
正八边形
正多边形的概念
当n>3时,必须同时满足以下两个条件:
(1)是各边相等,
(2)是各角相等.
两者缺一不可
如长方形各角相等,但各边不一定相等,菱形各边相等,但各角不一定相等,所以它们都不是正多边形。
判断一个n边形是正n边形的条件是:
菱形
矩形
正三角形
正方形
5、多边形分为___________和____________两类.
4、正多边形的_____相等,____相等.
3、从五边形的一个顶点出发可以画_____条对角线,它们将五边形分成______个三角形.
2、四边形有_____条对角线。五边形有______条对角线。四边形的一条对角线将它分成______个三角形.
1、n边形有______个顶点,_____边,有_____个角,有________个不共顶点外角.
n
n
n
n
2
5
2
3
2
边
角
凸多边形
凹多边形
课堂练习
1.下列不是凸多边形的是( )
A B C D
2. 下列图形中∠1是外角的是( )
A B C D
3.下列说法正确的是( )
A.一个多边形外角的个数与边数相同.
B. 一个多边形外角的个数是边数的二倍.
C.每个角都相等的多边形是正多边形.
D.每条边都相等的多边形是正多边形.
一试身手
C
1
1
1
1
D
B
练一练:
1、下列叙述正确的是( )
A、每条边都相等的多边形是正多边形。
B、如果画出多边形某一条边所在的直线, 这个多边形都在这条直线的同一侧,那么
它一定是凸多边形。
C、每个角都相等的多边形叫正多边形。
D、每条边、每个角都相等的多边形叫正多边形。
2、小学学过的下列图形中不可能是正多边形的是( )
A、三角形 B、正方形 C、四边形 D、梯形
D
D
把一个五边形锯去一个内角后得到是什么图形?请画图说明
①
②
③
解:五边形锯去一个内角后得到的图形可能是六边形,如图①;五边形,如图②;四边形,如图③
拓展题
将一个多边形(边数大于3)截去一个角,不同的截法会出现不同的结果:
(1)边数减1;(2)边数不变;(3)边数加1
小结
1、多边形的定义
在平面内,由一些线段首尾顺次相接组成的图形
2、多边形的内角
多边形相邻两边组成的角
3、多边形的外角
多边形的一边与它相邻边的反向延长线组成的角
4、多边形的对角线
连接多边形不相邻的两个顶点的线段
5、正多边形
各个角相等,各条边都相等的多边形
结论
n边形从一个顶点出发的对角线有(n-3)条,
把n边形分成(n - 2)个三角形(n≥3)
n边形共有对角线 条(n≥3)
