人教版八年级数学上册课件:13.3.1.1 等腰三角形的性质(共16张PPT)
文档属性
| 名称 | 人教版八年级数学上册课件:13.3.1.1 等腰三角形的性质(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 145.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:01:01 | ||
图片预览


文档简介
13.3.1-1等腰三角形性质
第13章 轴对称
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
前 言
学习目标
1、经历操作、发现、猜想、证明的过程,探索等腰三角形的性质,感受数学思考过程的条理性,培养学生的逻辑思维能力.
2、初步学会从数学的角度发现问题和提出问题,综合运用已有的知识解决新的问题.
重点难点
重点:等腰三角形的性质及应用。
难点:等腰三角形的性质证明。
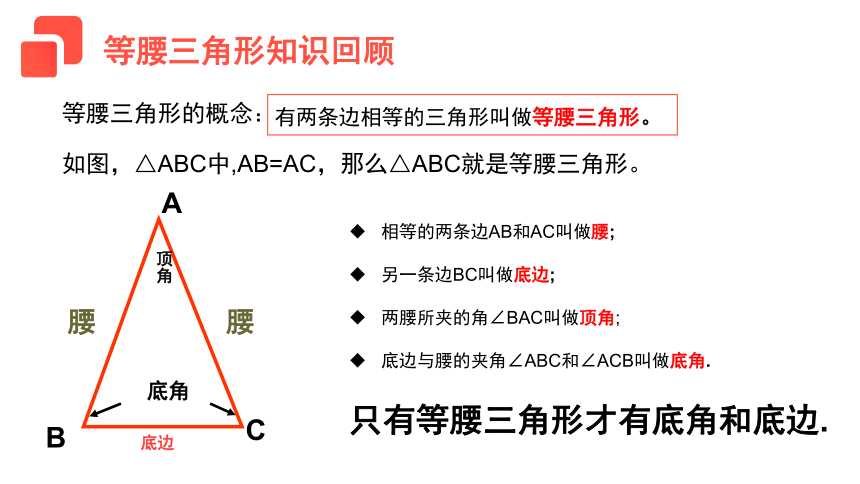
有两条边相等的三角形叫做等腰三角形。
相等的两条边AB和AC叫做腰;
另一条边BC叫做底边;
两腰所夹的角∠BAC叫做顶角;
底边与腰的夹角∠ABC和∠ACB叫做底角.
如图,△ABC中,AB=AC,那么△ABC就是等腰三角形。
只有等腰三角形才有底角和底边.
等腰三角形的概念:
A
B
C
腰
腰
底边
底角
顶角
等腰三角形知识回顾
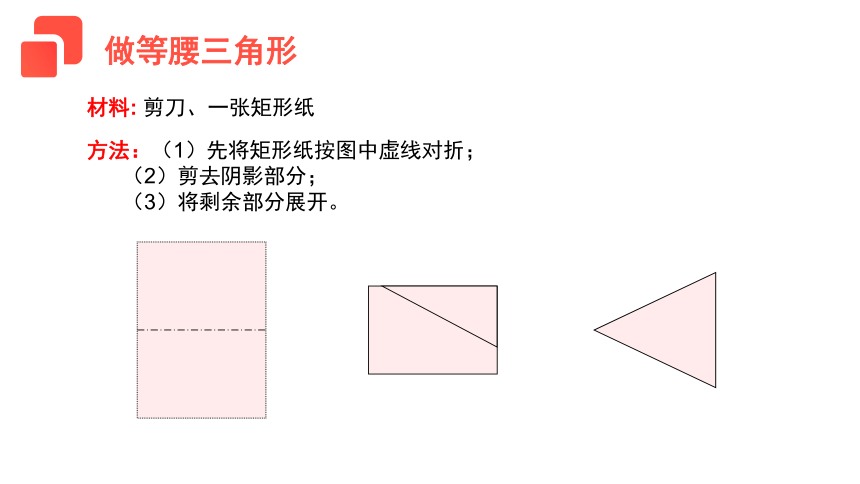
材料: 剪刀、一张矩形纸
方法:(1)先将矩形纸按图中虚线对折;
(2)剪去阴影部分;
(3)将剩余部分展开。
做等腰三角形
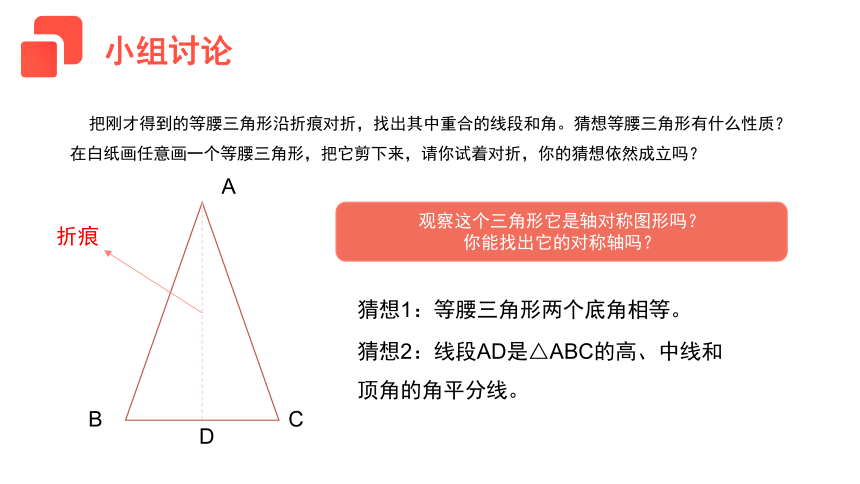
把刚才得到的等腰三角形沿折痕对折,找出其中重合的线段和角。猜想等腰三角形有什么性质?在白纸画任意画一个等腰三角形,把它剪下来,请你试着对折,你的猜想依然成立吗?
观察这个三角形它是轴对称图形吗?
你能找出它的对称轴吗?
A
B
C
D
猜想1:等腰三角形两个底角相等。
猜想2:线段AD是△ABC的高、中线和顶角的角平分线。
折痕
小组讨论
A
B
C
D
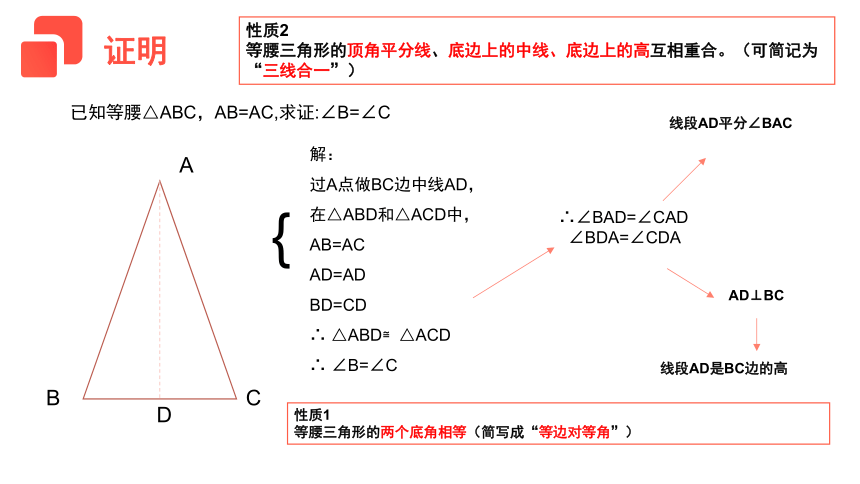
已知等腰△ABC,AB=AC,求证:∠B=∠C
解:
过A点做BC边中线AD,
在△ABD和△ACD中,
AB=AC
AD=AD
BD=CD
∴ △ABD≌△ACD
∴ ∠B=∠C
{
性质1
等腰三角形的两个底角相等(简写成“等边对等角”)
∴∠BAD=∠CAD
∠BDA=∠CDA
线段AD平分∠BAC
AD⊥BC
线段AD是BC边的高
性质2
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(可简记为“三线合一”)
证明
A
B
C
D
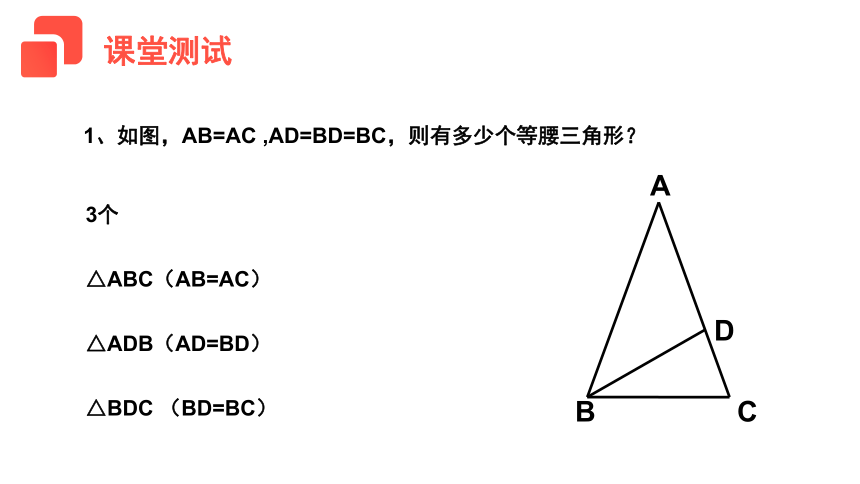
1、如图,AB=AC ,AD=BD=BC,则有多少个等腰三角形?
3个
△ABC(AB=AC)
△ADB(AD=BD)
△BDC (BD=BC)
课堂测试
2、判断(概念理解)
1.等腰三角形的角平分线、中线和高互相重合。
2.有一个角是60°的等腰三角形,其它两个内角也为60°。
3.等腰三角形的底角都是锐角。
4.钝角三角形不可能是等腰三角形。
课堂测试
3、在△ABC中,已知AB=AC,且∠B=75°,则∠C=___,∠A=____。
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵∠B=75° (已知)
∴∠C=75°
又∵∠A+∠B+∠C=180° (三角形内角和为180° )
∴∠A=180°- ∠B-∠C
∠A=30°
B
C
A
75°
30°
课堂测试
4、若等腰三角形的顶角为50°,则它的底角度数为(? ? ? ? )
A.40° B.50 ° C.60 ° D.65 °
【详解】
∵三角形为等腰三角形,且顶角为50°,
∴底角=(180°-50°)÷2=65°.
故选:D.
课堂测试
5、如果一个等腰三角形的两边长为4、9,则它的周长为( )
A.17 B.22 C.17或22 D.无法计算
【分析】
求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长;题目给出等腰三角形有两条边长为4和9,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【详解】
解:(1)若4为腰长,9为底边长,
由于4+4<9,则三角形不存在;
(2)若9为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为9+9+4=22.
故选:B.
课堂测试
6、等腰三角形的一个外角为110°,则它的顶角的度数是( )
A.40° B.70°
C.40°或70° D.以上答案均不对
【详解】
解:∵等腰三角形的一个外角是110°,
∴与这个外角相邻的内角是180°﹣110°=70°,
①当70°角是顶角时,它的顶角度数是70°,
②当70°角是底角时,它的顶角度数是180°﹣70°×2=40°,
综上所述,它的顶角度数是70°或40°.
故选:C.
课堂测试
7、已知等腰三角形的一边长为3cm,且它的周长为12cm,则它的底边长为 ( )
A.3cm B.6cm C.9cm D.3cm或6cm
【详解】
当3cm是等腰三角形的腰时,底边长=12-3×2=6cm,
∵3+3=6,不能构成三角形,
∴此种情况不存在;
当3cm是等腰三角形的底边时,腰长= =4.5cm.
∴底为3cm,
故选:A.
课堂测试
8、如图,△ABC中,已知,AB=AC,点D在CA的延长线上,∠DAB=50°,则∠B的度数为( )
A.25° B.30° C.40° D.45°
【详解】
∵AB=AC,
∴∠B=∠C,
∵∠DAB=∠B+∠C=50°,
∴∠B=25°,
故选:A.
课堂测试
② 顶角=180°-2×底角
③ 底角=(180°-顶角)÷2
④0°<顶角<180°
⑤0°<底角<90°
在等腰三角形中,
① 顶角+2×底角=180°
小结
感谢各位的仔细聆听
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
(等腰三角形性质)
第13章 轴对称
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
前 言
学习目标
1、经历操作、发现、猜想、证明的过程,探索等腰三角形的性质,感受数学思考过程的条理性,培养学生的逻辑思维能力.
2、初步学会从数学的角度发现问题和提出问题,综合运用已有的知识解决新的问题.
重点难点
重点:等腰三角形的性质及应用。
难点:等腰三角形的性质证明。
有两条边相等的三角形叫做等腰三角形。
相等的两条边AB和AC叫做腰;
另一条边BC叫做底边;
两腰所夹的角∠BAC叫做顶角;
底边与腰的夹角∠ABC和∠ACB叫做底角.
如图,△ABC中,AB=AC,那么△ABC就是等腰三角形。
只有等腰三角形才有底角和底边.
等腰三角形的概念:
A
B
C
腰
腰
底边
底角
顶角
等腰三角形知识回顾
材料: 剪刀、一张矩形纸
方法:(1)先将矩形纸按图中虚线对折;
(2)剪去阴影部分;
(3)将剩余部分展开。
做等腰三角形
把刚才得到的等腰三角形沿折痕对折,找出其中重合的线段和角。猜想等腰三角形有什么性质?在白纸画任意画一个等腰三角形,把它剪下来,请你试着对折,你的猜想依然成立吗?
观察这个三角形它是轴对称图形吗?
你能找出它的对称轴吗?
A
B
C
D
猜想1:等腰三角形两个底角相等。
猜想2:线段AD是△ABC的高、中线和顶角的角平分线。
折痕
小组讨论
A
B
C
D
已知等腰△ABC,AB=AC,求证:∠B=∠C
解:
过A点做BC边中线AD,
在△ABD和△ACD中,
AB=AC
AD=AD
BD=CD
∴ △ABD≌△ACD
∴ ∠B=∠C
{
性质1
等腰三角形的两个底角相等(简写成“等边对等角”)
∴∠BAD=∠CAD
∠BDA=∠CDA
线段AD平分∠BAC
AD⊥BC
线段AD是BC边的高
性质2
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(可简记为“三线合一”)
证明
A
B
C
D
1、如图,AB=AC ,AD=BD=BC,则有多少个等腰三角形?
3个
△ABC(AB=AC)
△ADB(AD=BD)
△BDC (BD=BC)
课堂测试
2、判断(概念理解)
1.等腰三角形的角平分线、中线和高互相重合。
2.有一个角是60°的等腰三角形,其它两个内角也为60°。
3.等腰三角形的底角都是锐角。
4.钝角三角形不可能是等腰三角形。
课堂测试
3、在△ABC中,已知AB=AC,且∠B=75°,则∠C=___,∠A=____。
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵∠B=75° (已知)
∴∠C=75°
又∵∠A+∠B+∠C=180° (三角形内角和为180° )
∴∠A=180°- ∠B-∠C
∠A=30°
B
C
A
75°
30°
课堂测试
4、若等腰三角形的顶角为50°,则它的底角度数为(? ? ? ? )
A.40° B.50 ° C.60 ° D.65 °
【详解】
∵三角形为等腰三角形,且顶角为50°,
∴底角=(180°-50°)÷2=65°.
故选:D.
课堂测试
5、如果一个等腰三角形的两边长为4、9,则它的周长为( )
A.17 B.22 C.17或22 D.无法计算
【分析】
求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长;题目给出等腰三角形有两条边长为4和9,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【详解】
解:(1)若4为腰长,9为底边长,
由于4+4<9,则三角形不存在;
(2)若9为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为9+9+4=22.
故选:B.
课堂测试
6、等腰三角形的一个外角为110°,则它的顶角的度数是( )
A.40° B.70°
C.40°或70° D.以上答案均不对
【详解】
解:∵等腰三角形的一个外角是110°,
∴与这个外角相邻的内角是180°﹣110°=70°,
①当70°角是顶角时,它的顶角度数是70°,
②当70°角是底角时,它的顶角度数是180°﹣70°×2=40°,
综上所述,它的顶角度数是70°或40°.
故选:C.
课堂测试
7、已知等腰三角形的一边长为3cm,且它的周长为12cm,则它的底边长为 ( )
A.3cm B.6cm C.9cm D.3cm或6cm
【详解】
当3cm是等腰三角形的腰时,底边长=12-3×2=6cm,
∵3+3=6,不能构成三角形,
∴此种情况不存在;
当3cm是等腰三角形的底边时,腰长= =4.5cm.
∴底为3cm,
故选:A.
课堂测试
8、如图,△ABC中,已知,AB=AC,点D在CA的延长线上,∠DAB=50°,则∠B的度数为( )
A.25° B.30° C.40° D.45°
【详解】
∵AB=AC,
∴∠B=∠C,
∵∠DAB=∠B+∠C=50°,
∴∠B=25°,
故选:A.
课堂测试
② 顶角=180°-2×底角
③ 底角=(180°-顶角)÷2
④0°<顶角<180°
⑤0°<底角<90°
在等腰三角形中,
① 顶角+2×底角=180°
小结
感谢各位的仔细聆听
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
(等腰三角形性质)
