人教版九年级数学下册 27.2.1相似三角形的判定(1) 课件(27张)
文档属性
| 名称 | 人教版九年级数学下册 27.2.1相似三角形的判定(1) 课件(27张) |  | |
| 格式 | pptx | ||
| 文件大小 | 301.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 07:03:32 | ||
图片预览


文档简介
27.2.1相似三角形的判定(1)
A
B
C
D
E
F
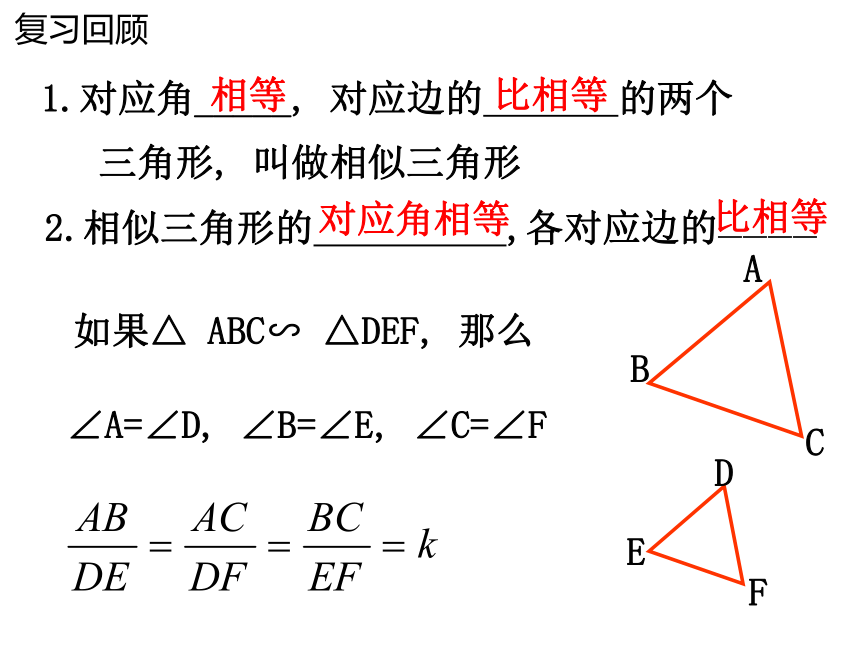
1.对应角_____, 对应边的 的两个
三角形, 叫做相似三角形
相等
比相等
2.相似三角形的 ,各对应边的————
对应角相等
比相等
如果△ ABC∽ △DEF, 那么
∠A=∠D, ∠B=∠E, ∠C=∠F
复习回顾
1、两个全等三角形一定相似吗?为什么?
相似比是多少?
2、两个直角三角形一定相似吗?为什么?
两个等腰直角三角形呢?
3、两个等腰三角形一定相似吗?为什么?
两个等边三角形呢?
300
450
复习回顾
C
E
D
B
A
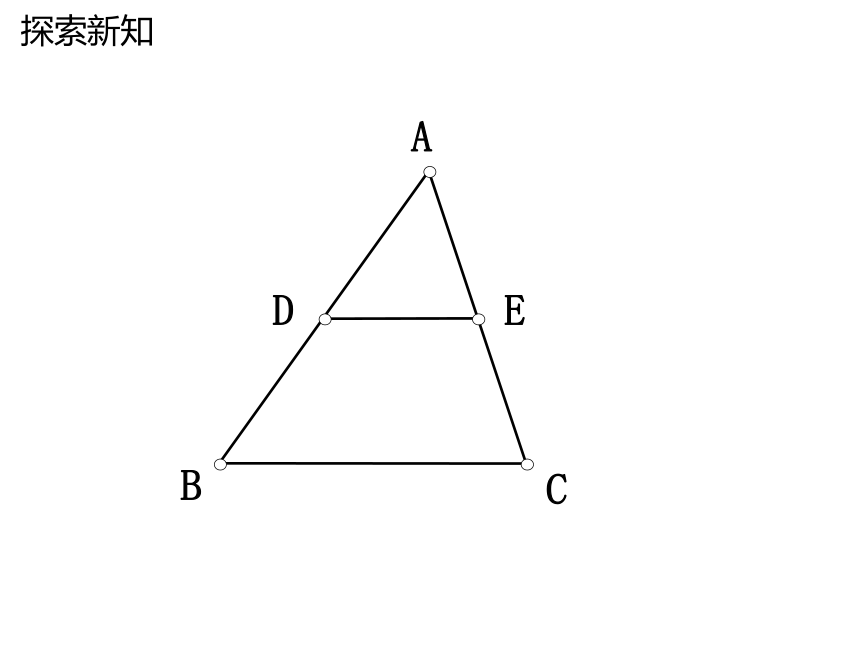
探索新知
L3
L4
L5
A
B
C
D
E
F
L1
L2
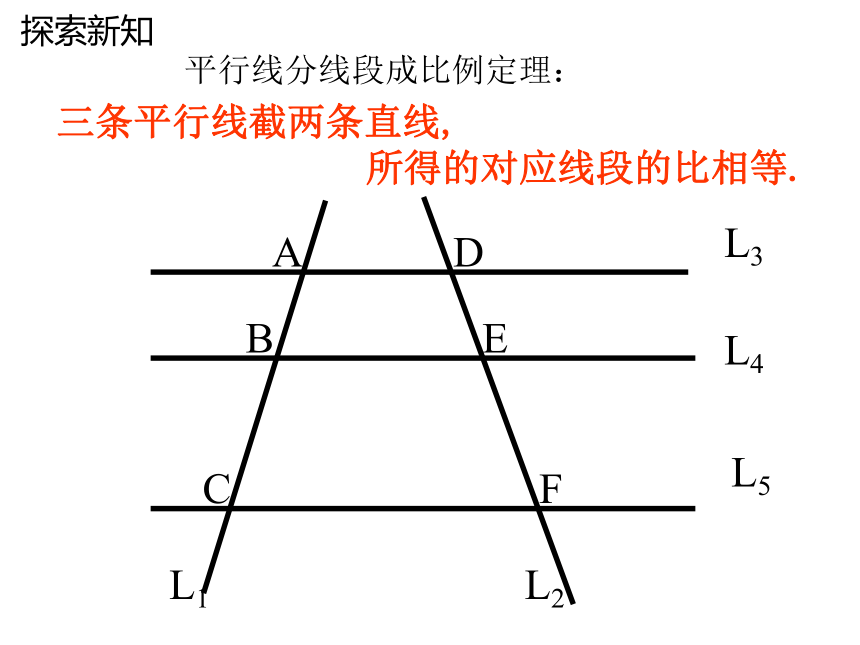
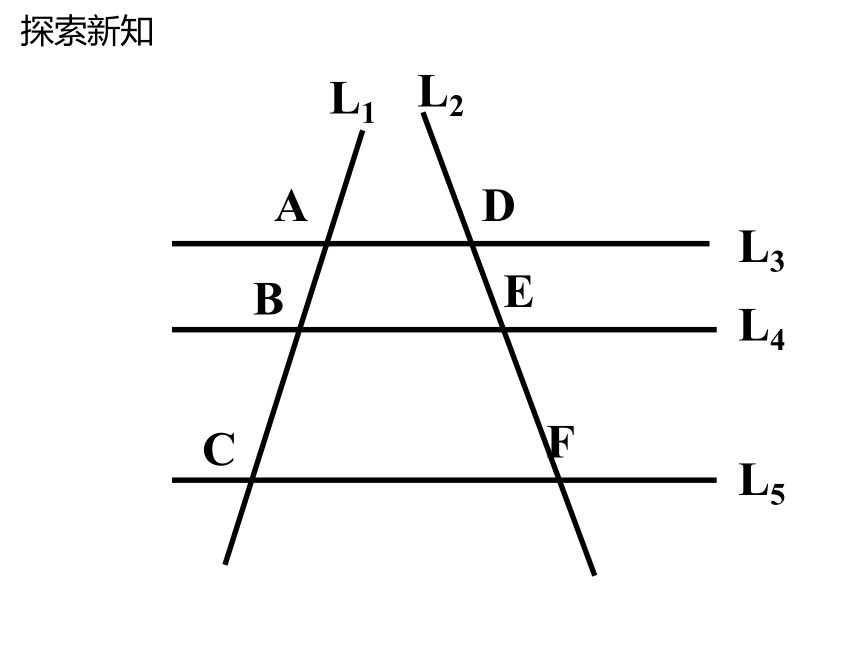
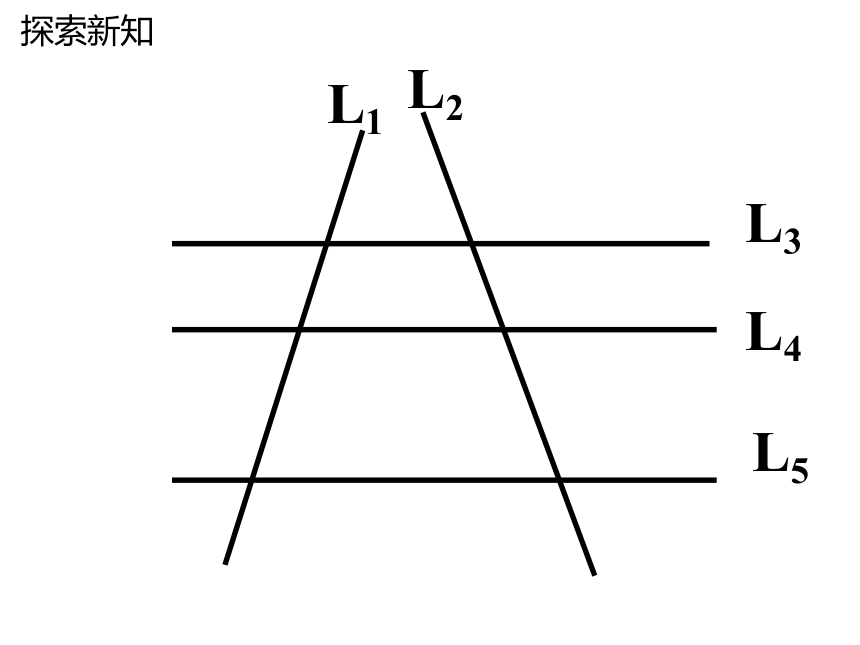
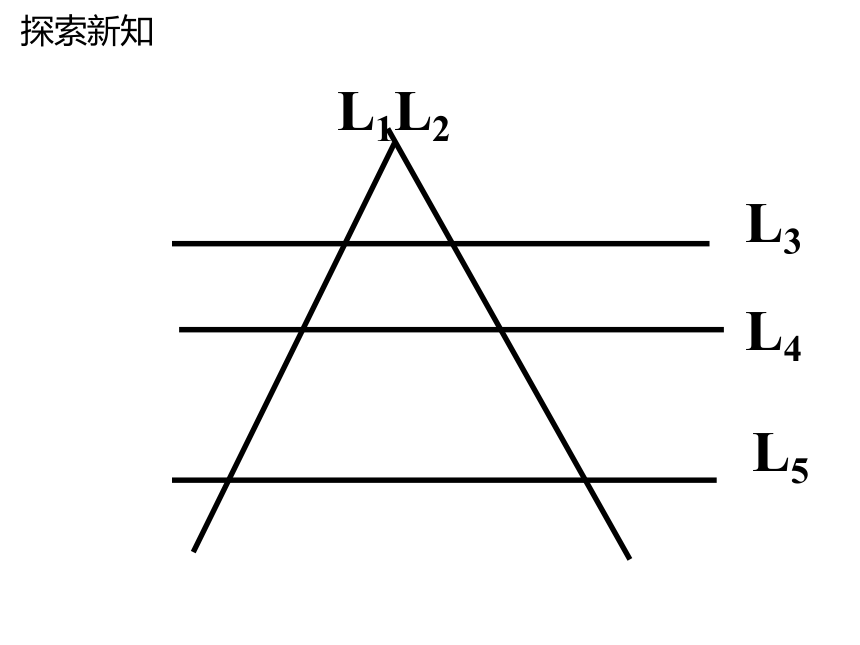
三条平行线截两条直线,
所得的对应线段的比相等.
平行线分线段成比例定理:
探索新知
L3
L4
L5
A
B
C
D
E
F
L1
L2
探索新知
L3
L4
L5
L1
L2
探索新知
L3
L4
L5
L1L2
探索新知
L3
L4
L5
L1
L2
探索新知
L3
L4
L5
L1
L2
探索新知
L3
L4
L5
L1
L2
探索新知
L3
L4
L5
L1
L2
探索新知
L1
L2
L3
L4
L5
探索新知
L1
L2
L3
L4
L5
L1
L2
L3
L4
L5
A
B
C
E
D
A
B
C
D
E
∵ DE∥BC
AD
AE
AC
AB
=
∵
∵ DE∥BC
AD
AE
AC
AB
=
∵
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等
探索新知
A
B
C
D
E
——
——
例1、判断题:
如图:DE∥BC, 下列各式是否正确
D:
——
——
=
AD
AE
AB
AC
( )
C:
——
——
=
AD
AC
AE
AB
( )
B:
——
——
=
AD
BD
AE
CE
( )
A:
AD
AB
=
AE
AC
( )
A
B
C
E
D
例2、填空题:
如图:DE∥BC,
已知:
2
=
——
AE
AC
—
5
=
——
AD
AB
求:
——
2
—
5
例题精讲
例3.已知:DE//BC, AB=4,AC=6,
BD=2 .求:AE=?
A
B
C
D
E
例题精讲
1、如图: 已知 DE∥BC,
AB = 8, AC = 10 ,
AE = 5,
求:AD的长。
EC
BC
DC
——
——
=
2、如图: 已知AB⊥BD,
ED⊥BD,垂足分别为
B、D。
求证:
AC
A
B
C
D
E
A
B
D
C
E
当堂练习
CB = 4,
BE
AB
=
A
A
B
C
D
E
C
1、如图: 已知 DE∥BC,
AB = 5, AC = 7 ,AD= 2,
求:AE的长。
B
D
E
2、已知 ∠A =∠E=60°
求:BD的长。
——
—
2
3
当堂检测
如图,在△ABC 中,DE//BC,
DE分别交AB,AC 于点D,E,
△ADE与△ABC有什么关系?
思考
DE是△ABC 的中位线,△ADE与△ABC有什么关系?
直觉告诉我们, △ADE与△ABC相似,我们通过相似的定义证明这个结论.
先证明两个三角形的对应角相等.
在△ADE与△ABC中, ∠A=∠A,
∵DE//BC,
∴∠ADE=∠B, ∠AED=∠C.
思考
再证明两个三角形的对应边的比相等.
过E作EF//AB,EF交BC于F点.
在平行四边形BFED中,DE=BF,DB=EF.
思考
F
即:△ADE与△ABC中,
∠A=∠A,∠ADE=∠B, ∠AED=∠C.
∴△ADE∽△ABC
思考
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
思考
已知:如图,AB∥EF ∥CD,
3
图中共有____对相似三角形。
△EOF∽△COD
AB∥EF
△AOB∽△FOE
AB∥CD
EF∥CD
△AOB∽△DOC
当堂练习
如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
当堂练习
如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.
解: 与△ABC相似的三角形有3个:
△ADE
△GFC
△GOE
A
B
C
D
E
F
G
O
当堂练习
如图在平行四边形ABCD中,E为AD上一点,连结CE并延长交BA的延长线于点F,
请找出相似的三角形并表示出来。
当堂练习
如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
(2)
A
D
B
E
C
解: (1)
DE ∥ BC
△ADE∽△ABC
∠AED=∠C=400.
△ADE∽△ABC
在△ADE中, ∠ADE=1800-400-450=950.
当堂练习
三条平行线截两条直线,
所得的对应线段的比相等.
1、平行线分线段成比例定理:
2、平行于三角形一边的直线截其他两边
(或两边的延长线),所得的对应线段的比相等
3、平行于三角形一边的直线和其他两边相交,
所构成的三角形与原三角形相似.
课堂小结
A
B
C
D
E
F
1.对应角_____, 对应边的 的两个
三角形, 叫做相似三角形
相等
比相等
2.相似三角形的 ,各对应边的————
对应角相等
比相等
如果△ ABC∽ △DEF, 那么
∠A=∠D, ∠B=∠E, ∠C=∠F
复习回顾
1、两个全等三角形一定相似吗?为什么?
相似比是多少?
2、两个直角三角形一定相似吗?为什么?
两个等腰直角三角形呢?
3、两个等腰三角形一定相似吗?为什么?
两个等边三角形呢?
300
450
复习回顾
C
E
D
B
A
探索新知
L3
L4
L5
A
B
C
D
E
F
L1
L2
三条平行线截两条直线,
所得的对应线段的比相等.
平行线分线段成比例定理:
探索新知
L3
L4
L5
A
B
C
D
E
F
L1
L2
探索新知
L3
L4
L5
L1
L2
探索新知
L3
L4
L5
L1L2
探索新知
L3
L4
L5
L1
L2
探索新知
L3
L4
L5
L1
L2
探索新知
L3
L4
L5
L1
L2
探索新知
L3
L4
L5
L1
L2
探索新知
L1
L2
L3
L4
L5
探索新知
L1
L2
L3
L4
L5
L1
L2
L3
L4
L5
A
B
C
E
D
A
B
C
D
E
∵ DE∥BC
AD
AE
AC
AB
=
∵
∵ DE∥BC
AD
AE
AC
AB
=
∵
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等
探索新知
A
B
C
D
E
——
——
例1、判断题:
如图:DE∥BC, 下列各式是否正确
D:
——
——
=
AD
AE
AB
AC
( )
C:
——
——
=
AD
AC
AE
AB
( )
B:
——
——
=
AD
BD
AE
CE
( )
A:
AD
AB
=
AE
AC
( )
A
B
C
E
D
例2、填空题:
如图:DE∥BC,
已知:
2
=
——
AE
AC
—
5
=
——
AD
AB
求:
——
2
—
5
例题精讲
例3.已知:DE//BC, AB=4,AC=6,
BD=2 .求:AE=?
A
B
C
D
E
例题精讲
1、如图: 已知 DE∥BC,
AB = 8, AC = 10 ,
AE = 5,
求:AD的长。
EC
BC
DC
——
——
=
2、如图: 已知AB⊥BD,
ED⊥BD,垂足分别为
B、D。
求证:
AC
A
B
C
D
E
A
B
D
C
E
当堂练习
CB = 4,
BE
AB
=
A
A
B
C
D
E
C
1、如图: 已知 DE∥BC,
AB = 5, AC = 7 ,AD= 2,
求:AE的长。
B
D
E
2、已知 ∠A =∠E=60°
求:BD的长。
——
—
2
3
当堂检测
如图,在△ABC 中,DE//BC,
DE分别交AB,AC 于点D,E,
△ADE与△ABC有什么关系?
思考
DE是△ABC 的中位线,△ADE与△ABC有什么关系?
直觉告诉我们, △ADE与△ABC相似,我们通过相似的定义证明这个结论.
先证明两个三角形的对应角相等.
在△ADE与△ABC中, ∠A=∠A,
∵DE//BC,
∴∠ADE=∠B, ∠AED=∠C.
思考
再证明两个三角形的对应边的比相等.
过E作EF//AB,EF交BC于F点.
在平行四边形BFED中,DE=BF,DB=EF.
思考
F
即:△ADE与△ABC中,
∠A=∠A,∠ADE=∠B, ∠AED=∠C.
∴△ADE∽△ABC
思考
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
思考
已知:如图,AB∥EF ∥CD,
3
图中共有____对相似三角形。
△EOF∽△COD
AB∥EF
△AOB∽△FOE
AB∥CD
EF∥CD
△AOB∽△DOC
当堂练习
如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
当堂练习
如图,△ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.
解: 与△ABC相似的三角形有3个:
△ADE
△GFC
△GOE
A
B
C
D
E
F
G
O
当堂练习
如图在平行四边形ABCD中,E为AD上一点,连结CE并延长交BA的延长线于点F,
请找出相似的三角形并表示出来。
当堂练习
如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;(2)求DE的长.
(2)
A
D
B
E
C
解: (1)
DE ∥ BC
△ADE∽△ABC
∠AED=∠C=400.
△ADE∽△ABC
在△ADE中, ∠ADE=1800-400-450=950.
当堂练习
三条平行线截两条直线,
所得的对应线段的比相等.
1、平行线分线段成比例定理:
2、平行于三角形一边的直线截其他两边
(或两边的延长线),所得的对应线段的比相等
3、平行于三角形一边的直线和其他两边相交,
所构成的三角形与原三角形相似.
课堂小结
