人教版七年级数学上册3.4.2实际问题问题与一元一次方问题探究4(电话计费问题)课件(34张)
文档属性
| 名称 | 人教版七年级数学上册3.4.2实际问题问题与一元一次方问题探究4(电话计费问题)课件(34张) |  | |
| 格式 | ppt | ||
| 文件大小 | 765.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 07:12:29 | ||
图片预览











文档简介
分段计费问题
———课本问题探究3
1、小明坐车早上上学,晚上回家需要做6次公共汽车,4次一元的,2次2元的。公交卡(IC卡)收费如下
IC卡: 1元 0.4元
2元 0.8元
请你帮小王算一算,小明用IC卡坐公共汽车可以省多少元?
2、王老师带30个学生去公园玩怎样买票省钱?300元够吗?
成人:15元/张
学生:10元/张
团体:10人以上7.5元/人
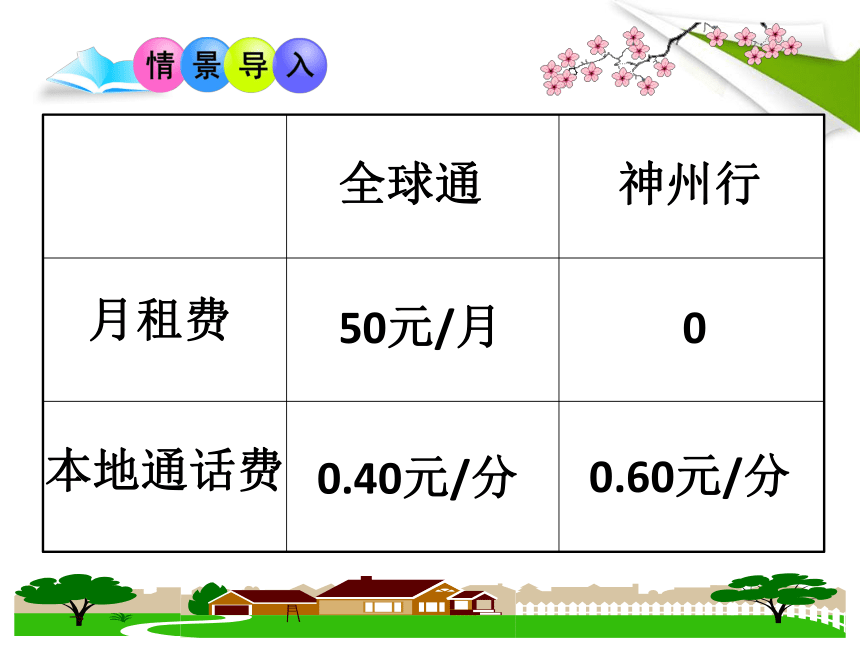
问题1:某移动通讯公司开设两种业务,“全球通”:先缴50元月租费,然后通话每分钟0.4元;“神州行”:不缴月租费,然后通话每分钟0.6元(本题的通话费均指本地通话),设某人一个月内通话时间为x分钟。
月租费
本地通话费
全球通
神州行
50元/月
0
0.40元/分
0.60元/分
(1)你能把两种方式的通话费用分别用含x的式子表示出来吗?
(1)你能把两种方式的通话费用分别用含x的式子表示出来吗?
解:设某人每月通话时间为x分钟,则每月的通话费用为:
“全球通”:50+0.4x(元)
“神州行”:0.6x(元)
(2)一个月内通话多少分钟时,两种费用一样?
(2)一个月内通话多少分钟时,两种费用一样?
解:设每月通话x分钟时,两种费用一样,列方程得50+0.4x=0.6x
解得x=250
答:一个月内通话250分钟时,两种费用一样。
(3)某人估计一个月内通话300分钟,应选择哪种方式更合算?
(3)某人估计一个月内通话300分钟,应选择哪种方式更合算?
解:(3)当x=300时,
“全球通”费用为:50+0.4×300=170(元)
“神州行”费用为:0.6×300=180(元)
答:当月通话时间为300分钟时,应该选择“全球通”更合算。
问题2:电话计费问题
下表中有两种移动电话计费方式。
被叫
免费
免费
方式一
方式二
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
58
88
150
350
0.25
0.19
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数)。根据上表,列表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费。
特别提示:
月使用费固定收;
主叫不超限定时间不再收费,主叫超时部分加收超时费;
被叫免费。
分析:(1)由上表可知,计费与主叫时间相关,计费时首先要看主叫是否超过限定时间。因此,考虑t的取值时,两个主叫限定时间150min和350min是不同时间范围的划分点。
t在不同时间范围内取值时,列表如下:
主叫时间t/min
方式一计费/元
方式二计费/元
t小于150
58
88
t=150
58
88
t大于150且小于350
58+0.25(t-150)
88
t=350
58+0.25(350-150)=108
88
t大于350
58+0.25(t-150)
88+0.19(t-350)
(2)观察(1)中的表,可以发现:主叫时间超出限定时间越长,计费越多,并且随着主叫时间的变化,按哪种方式的计费少也会变化。下面比较不同时间范围内方式一和方式二的计费情况。
主叫时间t/min
方式一
计费/元
方式二
计费/元
t小于150
t=150
t大于150且小于350
t=350
t大于350
58
58
58+0.25(t-150)
58+0.25(350-150)=108
88
88
88
88
58+0.25(t-150)
88+0.19(t-350)
①当t小于或等于150时,按方式一的计费少。
②当t从150增加到350时,按方式一的计费由58元增加到108元,而按方式二的计费一直是88元。因此,当t大于150并且小于350时,可能在某主叫时间按方式一和方式二的计费相等。列方程58+0.25(t-150)=88,解得t=270。
因此,如果主叫时间恰是270min,按两种方式的计费相等,都是88元;
如果主叫时间大于150min且小于270,按方式一的计费少于按方式二的计费(88元);
如果主叫时间大于270min且小于350min,按方式一的计费多于按方式二的计费(88元)。
综合以上的分析,可以发现:
_______时,选择方式一省钱;
_______时,选择方式二省钱。
请你选一些具体数字,通过计算验证你的发现是否正确。
综合以上的分析,可以发现:
t<270时,选择方式一省钱;
t>270时,选择方式二省钱。
请你选一些具体数字,通过计算验证你的发现是否正确。
1.某市居民生活用水基本价格为每吨2.4元,加上污水处理费每吨0.6元。为了节约用水,该市规定,若居民每月用水量超过规定量,那么超过规定部分的水的价格将按每吨5.0元收取,污水处理费按每吨1.0元收取。若该居民7月份用水20吨,共交水费96元,求每月规定用水量。
3、元阳出租车收费标准是起步价为5元,3千米后的价格为1.5元/千米,不足1千米的以1千米计算.
(1)若行驶x千米(x>3),试用式子表示应收多少的车费?
(2)我乘坐出租车行驶5.8千米,应付多少元?
(3)如果我付12.5元,那么出租车行驶了大约多少路程?
?
分析:
(1)根据题意:起步价5元,可行3千米(包括3千米);3千米以后每千米1.5元,列出代数式求解即可;
(2)根据不足1千米的以1千米计算可知5.8千米的价钱=6千米的价钱,代入(1)的解析式进行求解.
(3)将12.5元代入(1)的解析式进行求解即可解答.
解:(1)设费用为y,
∵某市出租车的收费标准为:起步价5元,3千米后的价格为1.5元/千米,
∴行驶x千米(x>3),
费用y=5+(x﹣3)×1.5
=1.5x+0.5元.
3、元阳出租车收费标准是起步价为5元,3千米后的价格为1.5元/千米,不足1千米的以1千米计算.
(1)若行驶x千米(x>3),试用式子表示应收多少的车费?
(2)不足1千米的以1千米计算可知5.8千米的价钱=6千米的价钱,
将x=6代入1.5x+0.5可得1.5×6+0.5=9.5元.
即乘坐出租车行驶5.8千米,应付9.5元.
(3)将y=12.5代入y=1.5x+0.5可得x=8.
即出租车行驶了大约8千米路程.
3、元阳出租车收费标准是起步价为5元,3千米后的价格为1.5元/千米,不足1千米的以1千米计算.
(2)我乘坐出租车行驶5.8千米,应付多少元?
(3)如果我付12.5元,那么出租车行驶了大约多少路程?
购票张数
1~50张
51~100张
100张以上
每张票的价格
13元
11元
9元
4.公园门票价格规定如下表:
某校初一(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果初一(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?
分析:若设初一(1)班有x,初一(2)有104-x人,题目已知x<50。根据总价钱即可列方程;
第二问利用算术方法即可解答;
第三问应尽量设计的能够享受优惠.
购票张数
1~50张
51~100张
100张以上
每张票的价格
13元
11元
9元
27.公园门票价格规定如下表:
某校初一(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果初一(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?
解:(1)设初一(1)班有x人,则有
13x+11(104﹣x)=1240,
解得:x=48.
即初一(1)班48人,初一(2)班56人;
?
(2)1240﹣104×9=304,
∴可省304元钱;
?(3)要想享受优惠,由(1)可知初一(1)班48人,只需多买3张,
51×11=561,48×13=624>561
∴48人买51人的票可以更省钱.
第一档电量
第二档电量
第三档电量
月用电量210度以下,每度价格0.52元
月用电量210度至350度,每度比第一档提价0.05元
月用电量350度以上,每度比第一档提价0.30元
1.(2012?)某省公布的居民用电阶梯电价听证方案如下:
例:若某户月用电量400度,则需交电费为
210×0.52+(350﹣210)×(0.52+0.05)+(400﹣350)
×(0.52+0.30)=230(元)
(1)分别计算出用电量为210度,350度时需要交纳的电费,
小华家5月份的电费为138.84元,
请你求出小华家5月份的用电量
第一档电量
第二档电量
第三档电量
月用电量210度以下,每度价格0.52元
月用电量210度至350度,每度比第一档提价0.05元
月用电量350度以上,每度比第一档提价0.30元
解:(1)用电量为210度时,需要交纳210×0.52=109.2元,
用电量为350度时,需要交纳2
10×0.52+(350﹣210)×(0.52+0.05)=189元,
故可得小华家5月份的用电量在第二档,
设小华家5月份的用电量为x,则
210×0.52+(x﹣210)×(0.52+0.05)=138.84
,
解得:x=262,即小华家5月份的用电量为262度.
———课本问题探究3
1、小明坐车早上上学,晚上回家需要做6次公共汽车,4次一元的,2次2元的。公交卡(IC卡)收费如下
IC卡: 1元 0.4元
2元 0.8元
请你帮小王算一算,小明用IC卡坐公共汽车可以省多少元?
2、王老师带30个学生去公园玩怎样买票省钱?300元够吗?
成人:15元/张
学生:10元/张
团体:10人以上7.5元/人
问题1:某移动通讯公司开设两种业务,“全球通”:先缴50元月租费,然后通话每分钟0.4元;“神州行”:不缴月租费,然后通话每分钟0.6元(本题的通话费均指本地通话),设某人一个月内通话时间为x分钟。
月租费
本地通话费
全球通
神州行
50元/月
0
0.40元/分
0.60元/分
(1)你能把两种方式的通话费用分别用含x的式子表示出来吗?
(1)你能把两种方式的通话费用分别用含x的式子表示出来吗?
解:设某人每月通话时间为x分钟,则每月的通话费用为:
“全球通”:50+0.4x(元)
“神州行”:0.6x(元)
(2)一个月内通话多少分钟时,两种费用一样?
(2)一个月内通话多少分钟时,两种费用一样?
解:设每月通话x分钟时,两种费用一样,列方程得50+0.4x=0.6x
解得x=250
答:一个月内通话250分钟时,两种费用一样。
(3)某人估计一个月内通话300分钟,应选择哪种方式更合算?
(3)某人估计一个月内通话300分钟,应选择哪种方式更合算?
解:(3)当x=300时,
“全球通”费用为:50+0.4×300=170(元)
“神州行”费用为:0.6×300=180(元)
答:当月通话时间为300分钟时,应该选择“全球通”更合算。
问题2:电话计费问题
下表中有两种移动电话计费方式。
被叫
免费
免费
方式一
方式二
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
58
88
150
350
0.25
0.19
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数)。根据上表,列表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费。
特别提示:
月使用费固定收;
主叫不超限定时间不再收费,主叫超时部分加收超时费;
被叫免费。
分析:(1)由上表可知,计费与主叫时间相关,计费时首先要看主叫是否超过限定时间。因此,考虑t的取值时,两个主叫限定时间150min和350min是不同时间范围的划分点。
t在不同时间范围内取值时,列表如下:
主叫时间t/min
方式一计费/元
方式二计费/元
t小于150
58
88
t=150
58
88
t大于150且小于350
58+0.25(t-150)
88
t=350
58+0.25(350-150)=108
88
t大于350
58+0.25(t-150)
88+0.19(t-350)
(2)观察(1)中的表,可以发现:主叫时间超出限定时间越长,计费越多,并且随着主叫时间的变化,按哪种方式的计费少也会变化。下面比较不同时间范围内方式一和方式二的计费情况。
主叫时间t/min
方式一
计费/元
方式二
计费/元
t小于150
t=150
t大于150且小于350
t=350
t大于350
58
58
58+0.25(t-150)
58+0.25(350-150)=108
88
88
88
88
58+0.25(t-150)
88+0.19(t-350)
①当t小于或等于150时,按方式一的计费少。
②当t从150增加到350时,按方式一的计费由58元增加到108元,而按方式二的计费一直是88元。因此,当t大于150并且小于350时,可能在某主叫时间按方式一和方式二的计费相等。列方程58+0.25(t-150)=88,解得t=270。
因此,如果主叫时间恰是270min,按两种方式的计费相等,都是88元;
如果主叫时间大于150min且小于270,按方式一的计费少于按方式二的计费(88元);
如果主叫时间大于270min且小于350min,按方式一的计费多于按方式二的计费(88元)。
综合以上的分析,可以发现:
_______时,选择方式一省钱;
_______时,选择方式二省钱。
请你选一些具体数字,通过计算验证你的发现是否正确。
综合以上的分析,可以发现:
t<270时,选择方式一省钱;
t>270时,选择方式二省钱。
请你选一些具体数字,通过计算验证你的发现是否正确。
1.某市居民生活用水基本价格为每吨2.4元,加上污水处理费每吨0.6元。为了节约用水,该市规定,若居民每月用水量超过规定量,那么超过规定部分的水的价格将按每吨5.0元收取,污水处理费按每吨1.0元收取。若该居民7月份用水20吨,共交水费96元,求每月规定用水量。
3、元阳出租车收费标准是起步价为5元,3千米后的价格为1.5元/千米,不足1千米的以1千米计算.
(1)若行驶x千米(x>3),试用式子表示应收多少的车费?
(2)我乘坐出租车行驶5.8千米,应付多少元?
(3)如果我付12.5元,那么出租车行驶了大约多少路程?
?
分析:
(1)根据题意:起步价5元,可行3千米(包括3千米);3千米以后每千米1.5元,列出代数式求解即可;
(2)根据不足1千米的以1千米计算可知5.8千米的价钱=6千米的价钱,代入(1)的解析式进行求解.
(3)将12.5元代入(1)的解析式进行求解即可解答.
解:(1)设费用为y,
∵某市出租车的收费标准为:起步价5元,3千米后的价格为1.5元/千米,
∴行驶x千米(x>3),
费用y=5+(x﹣3)×1.5
=1.5x+0.5元.
3、元阳出租车收费标准是起步价为5元,3千米后的价格为1.5元/千米,不足1千米的以1千米计算.
(1)若行驶x千米(x>3),试用式子表示应收多少的车费?
(2)不足1千米的以1千米计算可知5.8千米的价钱=6千米的价钱,
将x=6代入1.5x+0.5可得1.5×6+0.5=9.5元.
即乘坐出租车行驶5.8千米,应付9.5元.
(3)将y=12.5代入y=1.5x+0.5可得x=8.
即出租车行驶了大约8千米路程.
3、元阳出租车收费标准是起步价为5元,3千米后的价格为1.5元/千米,不足1千米的以1千米计算.
(2)我乘坐出租车行驶5.8千米,应付多少元?
(3)如果我付12.5元,那么出租车行驶了大约多少路程?
购票张数
1~50张
51~100张
100张以上
每张票的价格
13元
11元
9元
4.公园门票价格规定如下表:
某校初一(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果初一(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?
分析:若设初一(1)班有x,初一(2)有104-x人,题目已知x<50。根据总价钱即可列方程;
第二问利用算术方法即可解答;
第三问应尽量设计的能够享受优惠.
购票张数
1~50张
51~100张
100张以上
每张票的价格
13元
11元
9元
27.公园门票价格规定如下表:
某校初一(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果初一(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?
解:(1)设初一(1)班有x人,则有
13x+11(104﹣x)=1240,
解得:x=48.
即初一(1)班48人,初一(2)班56人;
?
(2)1240﹣104×9=304,
∴可省304元钱;
?(3)要想享受优惠,由(1)可知初一(1)班48人,只需多买3张,
51×11=561,48×13=624>561
∴48人买51人的票可以更省钱.
第一档电量
第二档电量
第三档电量
月用电量210度以下,每度价格0.52元
月用电量210度至350度,每度比第一档提价0.05元
月用电量350度以上,每度比第一档提价0.30元
1.(2012?)某省公布的居民用电阶梯电价听证方案如下:
例:若某户月用电量400度,则需交电费为
210×0.52+(350﹣210)×(0.52+0.05)+(400﹣350)
×(0.52+0.30)=230(元)
(1)分别计算出用电量为210度,350度时需要交纳的电费,
小华家5月份的电费为138.84元,
请你求出小华家5月份的用电量
第一档电量
第二档电量
第三档电量
月用电量210度以下,每度价格0.52元
月用电量210度至350度,每度比第一档提价0.05元
月用电量350度以上,每度比第一档提价0.30元
解:(1)用电量为210度时,需要交纳210×0.52=109.2元,
用电量为350度时,需要交纳2
10×0.52+(350﹣210)×(0.52+0.05)=189元,
故可得小华家5月份的用电量在第二档,
设小华家5月份的用电量为x,则
210×0.52+(x﹣210)×(0.52+0.05)=138.84
,
解得:x=262,即小华家5月份的用电量为262度.
