人教版七年级数学上册4.2--直线、射线、线段(2)课件(17张)
文档属性
| 名称 | 人教版七年级数学上册4.2--直线、射线、线段(2)课件(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 629.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:00 | ||
图片预览



文档简介
4.2 直线、射线、线段(2)
第四章 几何图形初步
小明
小华
我比你高!
你哪有我高啊!
比一比
服了吧!
喔,原来你比我高!
小明
小华
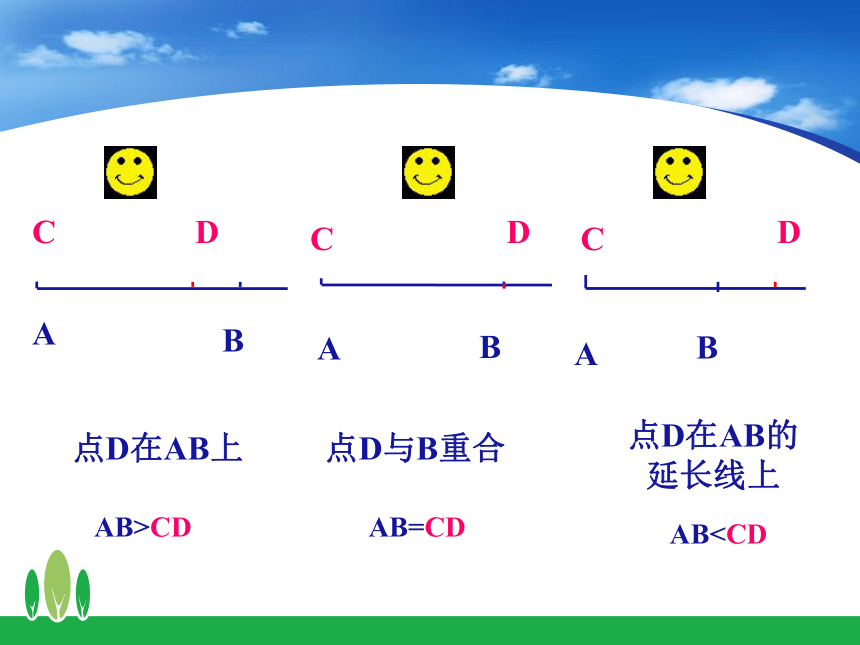
点D在AB的延长线上
点D与B重合
点D在AB上
AB>CD
AB=CD
ABB
A
C
D
B
C
A
A
C
B
D
D
(二)概念延伸,思维提升
A(C)
B
D
图1
A(C)
B
D
图2
A(C)
B(D)
图3
练习1:判断线段AB和CD的大小.
(1)如图1,线段AB和CD的大小关系是AB CD;
(2)如图2,线段AB和CD的大小关系是AB CD;
(3)如图3,线段AB和CD的大小关系是AB CD.
<
>
=
(一)开门见山,引入新知
【问题1】老师手里的纸上有一条线段,你能在你的本上作出一条同样长的线段吗?
?
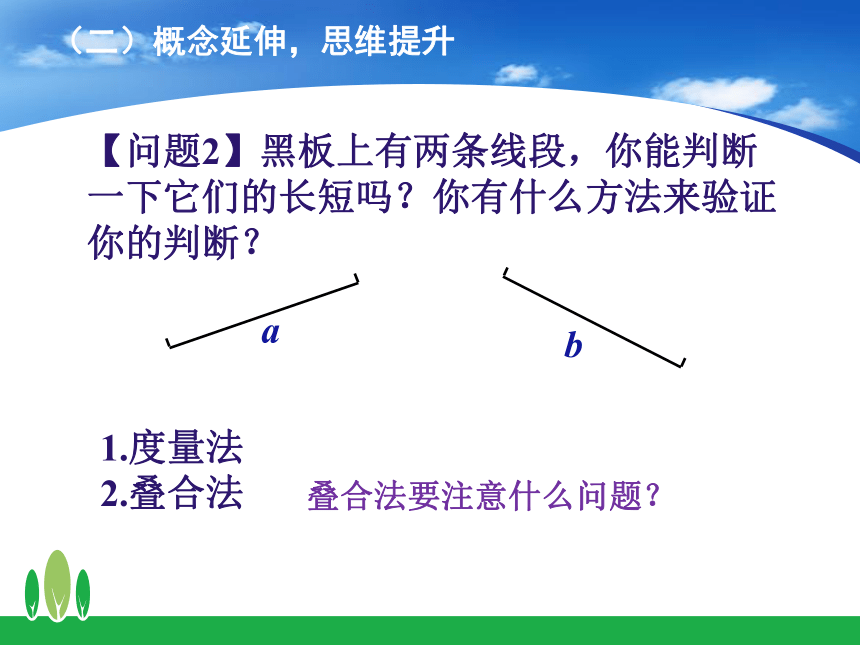
(二)概念延伸,思维提升
【问题2】黑板上有两条线段,你能判断一下它们的长短吗?你有什么方法来验证你的判断?
1.度量法
2.叠合法
a
b
叠合法要注意什么问题?
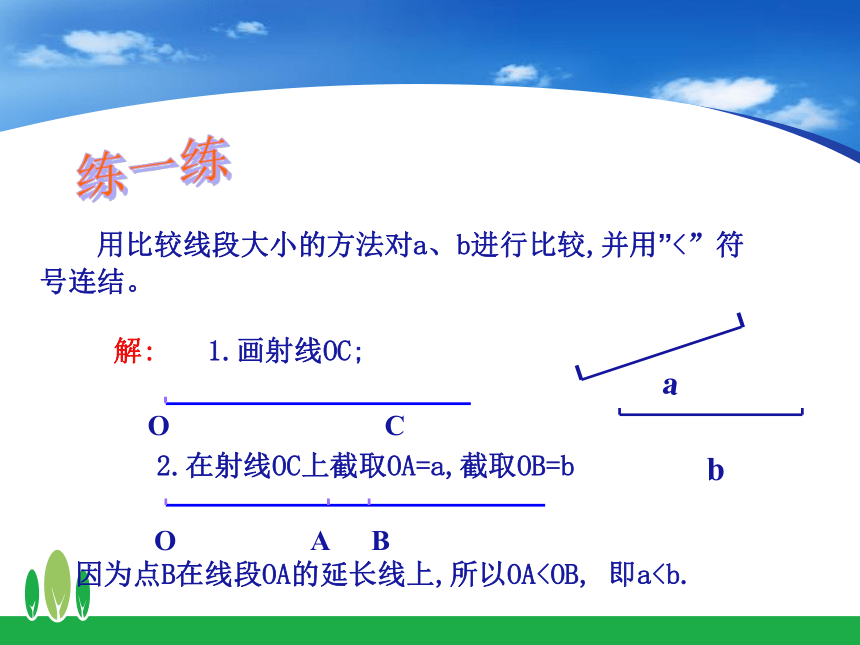
用比较线段大小的方法对a、b进行比较,并用”<”符号连结。
1.画射线OC;
2.在射线OC上截取OA=a,截取OB=b
解:
因为点B在线段OA的延长线上,所以OAb
a
练一练
O
C
O
B
A
(二)概念延伸,思维提升
【问题3】如图,线段AB和AC的大小关系是怎样的?线段AC与线段AB的差是哪条线段?你还能从图中观察出其他线段间的和、差关系吗?
A
B
C
(1) AB(2) AC-AB=BC
AC-BC=AB
BC+AB=AC
中点的概念:
点M把线段AB分成相等的两条线段AM和BM,点M叫做线段AB的中点。
A
B
M
AM
=
BM
=
-
2
1
AB
AB=2AM AB=2BM
【问题4】如图,已知线段a和线段b,怎样通过作图得到a与b的和、a与b的差呢?
(二)概念延伸,思维提升
b
a
B
C
a
b
A
P
B
C
a
b
A
P
AC=a+b
BC=a-b
【问题5】如图,已知线段a,求作线段AB=2a.
a
B
C
a
A
P
AC=2a
a
点B把线段AC分成相等的两条线段AB与BC,点B叫做线段AC的中点,可知AB=BC= AB.
1
2
(二)概念延伸,思维提升
那么什么叫做三等分点?四等分点呢?
(三)练习巩固,深化新知
练习3:如图,已知线段a、b,画一条线段使它等于2a-b.
a
b
(1)
(2)
(3)
练习2:估计下列图形中AB、AC的大小关系,再用刻度尺或圆规检验你的估计.
A
B
C
A
A
B
B
C
C
(1).两点之间的线段叫做这两点间的距离( )
(2).如果点 M是线段AB 的中点,那么AM=BM =AB ( )
(3).如果 AM =AB ,那么点M 是AB 的中点 ( )
1.判断题
(四)猜想验证,拓展新知
A
B
【问题6】如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短线路.
1. 两点的所有连线中,线段最短. 简单地说:两点之间,线段最短.
2. 连接两点间的线段的长度,叫做这两点的距离.
2.如图,把河道由弯曲改直,根据__________说明这样做能缩短航道.
(五)课堂小结,布置作业
【问题7】这节课你学到了什么?
画一条线段等于已知线段
线段比较大小
线段的和、差、分点(中点、三等分点等)
两点之间线段最短
两点的距离定义
【作业】教科书第129~130页习题4.2第5~8题.
学习的进步在于持之以恒
第四章 几何图形初步
小明
小华
我比你高!
你哪有我高啊!
比一比
服了吧!
喔,原来你比我高!
小明
小华
点D在AB的延长线上
点D与B重合
点D在AB上
AB>CD
AB=CD
AB
A
C
D
B
C
A
A
C
B
D
D
(二)概念延伸,思维提升
A(C)
B
D
图1
A(C)
B
D
图2
A(C)
B(D)
图3
练习1:判断线段AB和CD的大小.
(1)如图1,线段AB和CD的大小关系是AB CD;
(2)如图2,线段AB和CD的大小关系是AB CD;
(3)如图3,线段AB和CD的大小关系是AB CD.
<
>
=
(一)开门见山,引入新知
【问题1】老师手里的纸上有一条线段,你能在你的本上作出一条同样长的线段吗?
?
(二)概念延伸,思维提升
【问题2】黑板上有两条线段,你能判断一下它们的长短吗?你有什么方法来验证你的判断?
1.度量法
2.叠合法
a
b
叠合法要注意什么问题?
用比较线段大小的方法对a、b进行比较,并用”<”符号连结。
1.画射线OC;
2.在射线OC上截取OA=a,截取OB=b
解:
因为点B在线段OA的延长线上,所以OA
a
练一练
O
C
O
B
A
(二)概念延伸,思维提升
【问题3】如图,线段AB和AC的大小关系是怎样的?线段AC与线段AB的差是哪条线段?你还能从图中观察出其他线段间的和、差关系吗?
A
B
C
(1) AB
AC-BC=AB
BC+AB=AC
中点的概念:
点M把线段AB分成相等的两条线段AM和BM,点M叫做线段AB的中点。
A
B
M
AM
=
BM
=
-
2
1
AB
AB=2AM AB=2BM
【问题4】如图,已知线段a和线段b,怎样通过作图得到a与b的和、a与b的差呢?
(二)概念延伸,思维提升
b
a
B
C
a
b
A
P
B
C
a
b
A
P
AC=a+b
BC=a-b
【问题5】如图,已知线段a,求作线段AB=2a.
a
B
C
a
A
P
AC=2a
a
点B把线段AC分成相等的两条线段AB与BC,点B叫做线段AC的中点,可知AB=BC= AB.
1
2
(二)概念延伸,思维提升
那么什么叫做三等分点?四等分点呢?
(三)练习巩固,深化新知
练习3:如图,已知线段a、b,画一条线段使它等于2a-b.
a
b
(1)
(2)
(3)
练习2:估计下列图形中AB、AC的大小关系,再用刻度尺或圆规检验你的估计.
A
B
C
A
A
B
B
C
C
(1).两点之间的线段叫做这两点间的距离( )
(2).如果点 M是线段AB 的中点,那么AM=BM =AB ( )
(3).如果 AM =AB ,那么点M 是AB 的中点 ( )
1.判断题
(四)猜想验证,拓展新知
A
B
【问题6】如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短线路.
1. 两点的所有连线中,线段最短. 简单地说:两点之间,线段最短.
2. 连接两点间的线段的长度,叫做这两点的距离.
2.如图,把河道由弯曲改直,根据__________说明这样做能缩短航道.
(五)课堂小结,布置作业
【问题7】这节课你学到了什么?
画一条线段等于已知线段
线段比较大小
线段的和、差、分点(中点、三等分点等)
两点之间线段最短
两点的距离定义
【作业】教科书第129~130页习题4.2第5~8题.
学习的进步在于持之以恒
