人教版数学八年级下册课件18.1.2:平行四边形的判定(共19张PPT)
文档属性
| 名称 | 人教版数学八年级下册课件18.1.2:平行四边形的判定(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 08:54:31 | ||
图片预览





文档简介
第十八章 平行四边形
平行四边形的判定
BY YUSHEN
BY YUSHEN
目录
学习目标
LEARNING OBJECTIVES
01
1.平行四边形判定方法及应用。
2.综合运用平行四边形的判定和性质解决实际问题。
重点
A KEY
02
平行四边形判定方法及应用。
难点
DIFFICULTY
03
综合运用平行四边形的判定和性质解决实际问题。
BY YUSHEN
学习目标
01
BY YUSHEN
平行四边形知识点回顾
01
两组对边分别平行的四边形叫做平行四边形。
A
B
D
C
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
概念:
几何描述:
性质:
平行四边形对边相等
平行四边形对角线互相平分
平行四边形对角相等
BY YUSHEN
平行四边形判定
01
A
B
D
C
平行四边形的性质:
平行四边形对边相等
平行四边形对角线互相平分
根据逆命题内容,尝试依次画出四边形,它们是平行四边形吗?
平行四边形对角相等
平行四边形性质的逆命题:
两组对边分别相等的四边形是平行四边形。
两组对角分别相等的四边形是平行四边形。
对角线互相平分的四边形是平行四边形。
BY YUSHEN
探索与证明
01
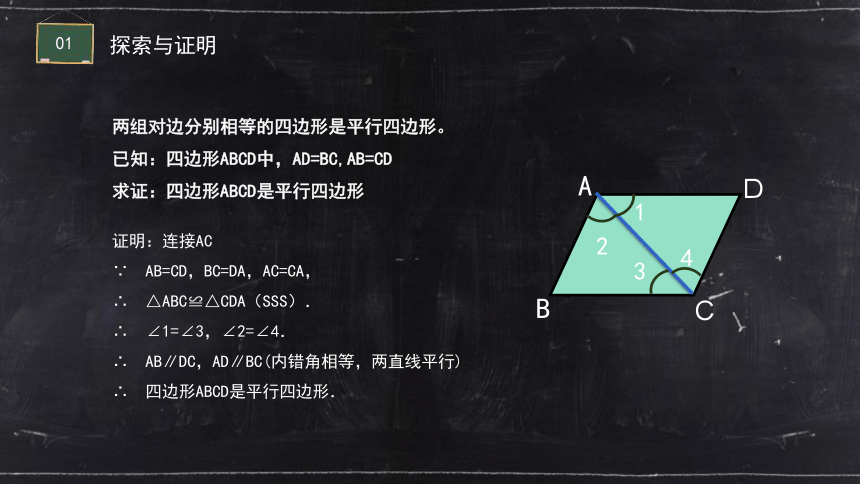
两组对边分别相等的四边形是平行四边形。
已知:四边形ABCD中,AD=BC,AB=CD
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
证明:连接AC
∵ AB=CD,BC=DA,AC=CA,
∴ △ABC≌△CDA(SSS).
∴ ∠1=∠3,∠2=∠4.
∴ AB∥DC,AD∥BC(内错角相等,两直线平行)
∴ 四边形ABCD是平行四边形.
BY YUSHEN
探索与证明
01
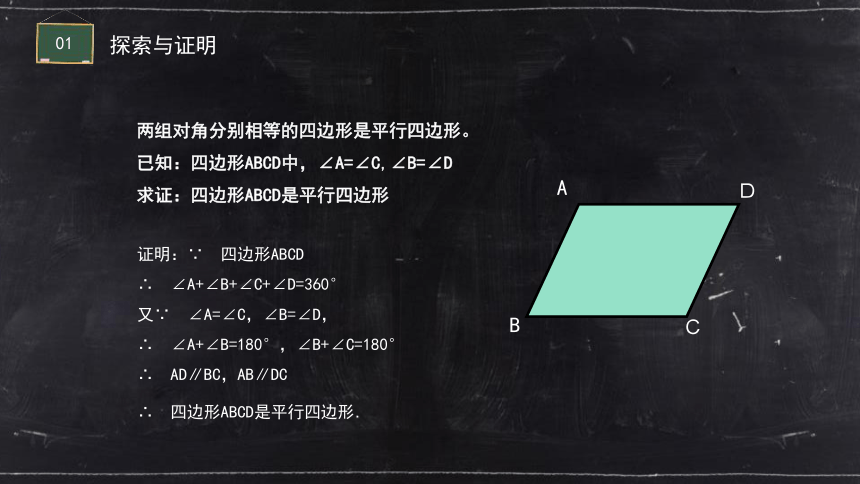
两组对角分别相等的四边形是平行四边形。
已知:四边形ABCD中,∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
A
B
D
C
证明:∵ 四边形ABCD
∴ ∠A+∠B+∠C+∠D=360°
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,∠B+∠C=180°
∴ AD∥BC,AB∥DC
∴ 四边形ABCD是平行四边形.
BY YUSHEN
探索与证明
01
对角线互相平分的四边形是平行四边形。
已知:四边形ABCD中,AO=OC,BO=DO
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
O
证明:∵ AO=OC,∠AOD = ∠COB,DO=BO ,
∴ △AOD≌△COB(SAS).
∴ ∠1=∠3 ∴ AD∥BC
同理 △AOB≌△COD(SAS).
∴ ∠2=∠4.∴ AB∥DC
∴ 四边形ABCD是平行四边形.
BY YUSHEN
小结
01
文字语言
图形语言
几何语言
定义法
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是平行四边形
判定方法1
两组对边分别相等的四边形是平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形
判定方法2
两组对角分别相等的四边形是平行四边形
∵∠A= ∠C, ∠B= ∠D,
∴四边形ABCD是平行四边形
判定方法3
对角线互相平分的四边形是平行四边形
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
BY YUSHEN
重点
02
BY YUSHEN
练一练
02
1.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
【答案】A
【详解】
解:由已知可得AO=CO,BO=DO,所以四边形ABCD是平行四边形,依据是对角线互相平分的四边形是平行四边形.
故选:A.
BY YUSHEN
?
【答案】C
【详解】
A、∵∠ADB=∠CBD,∴AD∥BC,∵AB∥CD,∴四边形ABCD是平行四边形,故此选项不合题意;
B、∵∠ADB=∠CBD,∴AD∥BC,∵∠DAB=∠BCD∴∠BAD+∠ABC=∠ADC+∠BCD=180°,∴∠ABC=∠ADC,∴四边形ABCD是平行四边形,故此选项不符合题意;
C、∠DAB=∠BCD,AB=CD不能判定四边形ABCD是平行四边形,故此选项符合题意;
D、∵∠ABD=∠CDB,∠AOB=∠COD,OA=OC,∴△AOB≌△COD(AAS),
∴OB=OC,∴四边形ABCD为平行四边形,故此选项不合题意;故选:C.
练一练
02
BY YUSHEN
练一练
02
3.已知E、F分别是平行四边形ABCD中BD上的点,且BE=DF,试说明:四边形AECF是平行四边形。
?
BY YUSHEN
练一练
02
4.如图,在平行四边形 ABCD中,点E、F在对角线BD上,且BE=DF.
(1)求证:AE=CF;
(2)求证:四边形AECF是平行四边形.
?
BY YUSHEN
练一练
02
4.如图,在平行四边形 ABCD中,点E、F在对角线BD上,且BE=DF.
(1)求证:AE=CF;
(2)求证:四边形AECF是平行四边形.
【详解】
(2)∵△ABE≌△CDF,
∴∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.
BY YUSHEN
练一练
02
?
?
BY YUSHEN
练一练
02
?
?
PART 03
BY YUSHEN
课后回顾
平行四边形的判定方法
01
平行四边形判定证明
02
利用平行四边形的性质
和判定解决实际问题
03
谢谢同学倾听
BY YUSHEN
平行四边形的判定
BY YUSHEN
BY YUSHEN
目录
学习目标
LEARNING OBJECTIVES
01
1.平行四边形判定方法及应用。
2.综合运用平行四边形的判定和性质解决实际问题。
重点
A KEY
02
平行四边形判定方法及应用。
难点
DIFFICULTY
03
综合运用平行四边形的判定和性质解决实际问题。
BY YUSHEN
学习目标
01
BY YUSHEN
平行四边形知识点回顾
01
两组对边分别平行的四边形叫做平行四边形。
A
B
D
C
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
概念:
几何描述:
性质:
平行四边形对边相等
平行四边形对角线互相平分
平行四边形对角相等
BY YUSHEN
平行四边形判定
01
A
B
D
C
平行四边形的性质:
平行四边形对边相等
平行四边形对角线互相平分
根据逆命题内容,尝试依次画出四边形,它们是平行四边形吗?
平行四边形对角相等
平行四边形性质的逆命题:
两组对边分别相等的四边形是平行四边形。
两组对角分别相等的四边形是平行四边形。
对角线互相平分的四边形是平行四边形。
BY YUSHEN
探索与证明
01
两组对边分别相等的四边形是平行四边形。
已知:四边形ABCD中,AD=BC,AB=CD
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
证明:连接AC
∵ AB=CD,BC=DA,AC=CA,
∴ △ABC≌△CDA(SSS).
∴ ∠1=∠3,∠2=∠4.
∴ AB∥DC,AD∥BC(内错角相等,两直线平行)
∴ 四边形ABCD是平行四边形.
BY YUSHEN
探索与证明
01
两组对角分别相等的四边形是平行四边形。
已知:四边形ABCD中,∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
A
B
D
C
证明:∵ 四边形ABCD
∴ ∠A+∠B+∠C+∠D=360°
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,∠B+∠C=180°
∴ AD∥BC,AB∥DC
∴ 四边形ABCD是平行四边形.
BY YUSHEN
探索与证明
01
对角线互相平分的四边形是平行四边形。
已知:四边形ABCD中,AO=OC,BO=DO
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
O
证明:∵ AO=OC,∠AOD = ∠COB,DO=BO ,
∴ △AOD≌△COB(SAS).
∴ ∠1=∠3 ∴ AD∥BC
同理 △AOB≌△COD(SAS).
∴ ∠2=∠4.∴ AB∥DC
∴ 四边形ABCD是平行四边形.
BY YUSHEN
小结
01
文字语言
图形语言
几何语言
定义法
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是平行四边形
判定方法1
两组对边分别相等的四边形是平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形
判定方法2
两组对角分别相等的四边形是平行四边形
∵∠A= ∠C, ∠B= ∠D,
∴四边形ABCD是平行四边形
判定方法3
对角线互相平分的四边形是平行四边形
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
BY YUSHEN
重点
02
BY YUSHEN
练一练
02
1.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
【答案】A
【详解】
解:由已知可得AO=CO,BO=DO,所以四边形ABCD是平行四边形,依据是对角线互相平分的四边形是平行四边形.
故选:A.
BY YUSHEN
?
【答案】C
【详解】
A、∵∠ADB=∠CBD,∴AD∥BC,∵AB∥CD,∴四边形ABCD是平行四边形,故此选项不合题意;
B、∵∠ADB=∠CBD,∴AD∥BC,∵∠DAB=∠BCD∴∠BAD+∠ABC=∠ADC+∠BCD=180°,∴∠ABC=∠ADC,∴四边形ABCD是平行四边形,故此选项不符合题意;
C、∠DAB=∠BCD,AB=CD不能判定四边形ABCD是平行四边形,故此选项符合题意;
D、∵∠ABD=∠CDB,∠AOB=∠COD,OA=OC,∴△AOB≌△COD(AAS),
∴OB=OC,∴四边形ABCD为平行四边形,故此选项不合题意;故选:C.
练一练
02
BY YUSHEN
练一练
02
3.已知E、F分别是平行四边形ABCD中BD上的点,且BE=DF,试说明:四边形AECF是平行四边形。
?
BY YUSHEN
练一练
02
4.如图,在平行四边形 ABCD中,点E、F在对角线BD上,且BE=DF.
(1)求证:AE=CF;
(2)求证:四边形AECF是平行四边形.
?
BY YUSHEN
练一练
02
4.如图,在平行四边形 ABCD中,点E、F在对角线BD上,且BE=DF.
(1)求证:AE=CF;
(2)求证:四边形AECF是平行四边形.
【详解】
(2)∵△ABE≌△CDF,
∴∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.
BY YUSHEN
练一练
02
?
?
BY YUSHEN
练一练
02
?
?
PART 03
BY YUSHEN
课后回顾
平行四边形的判定方法
01
平行四边形判定证明
02
利用平行四边形的性质
和判定解决实际问题
03
谢谢同学倾听
BY YUSHEN
