人教版数学九年级 下册28.1.2特殊角的三角函数值及用计算器求锐角三角函数值课件(26张PPT)
文档属性
| 名称 | 人教版数学九年级 下册28.1.2特殊角的三角函数值及用计算器求锐角三角函数值课件(26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 257.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 08:52:54 | ||
图片预览



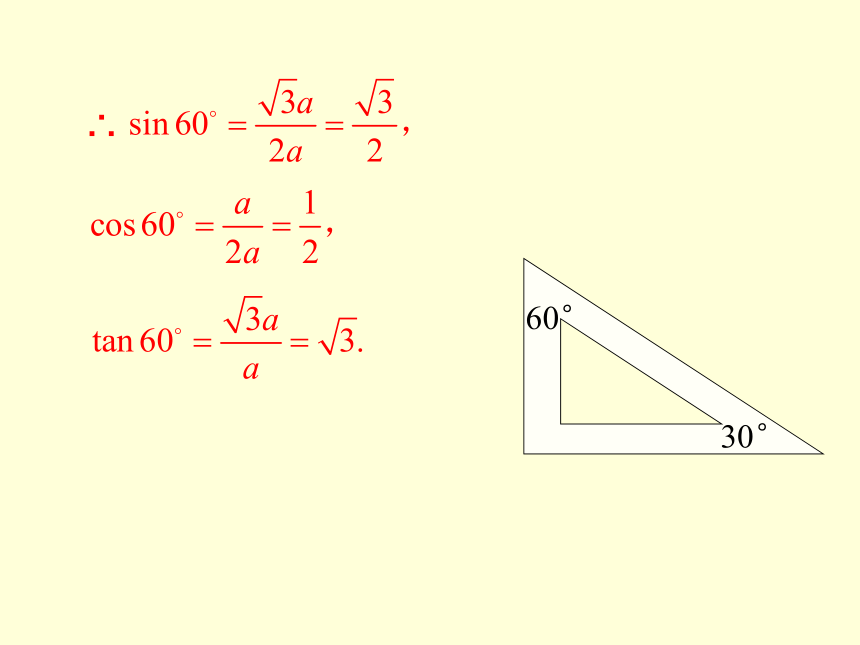
文档简介
导入新课
讲授新课
当堂练习
课堂小结
28.1 锐角三角函数
第二十八章 锐角三角函数
第3课时 特殊角的三角函数值
及用计算器求角的三角函数值
学习目标
1. 运用三角函数的知识,自主探索,推导出30°、
45°、60°角的三角函数值. (重点)
2. 会使用科学计算器求锐角的三角函数值.
3. 熟记三个特殊锐角的三角函数值,并能准确地加
以运用. (难点)
导入新课
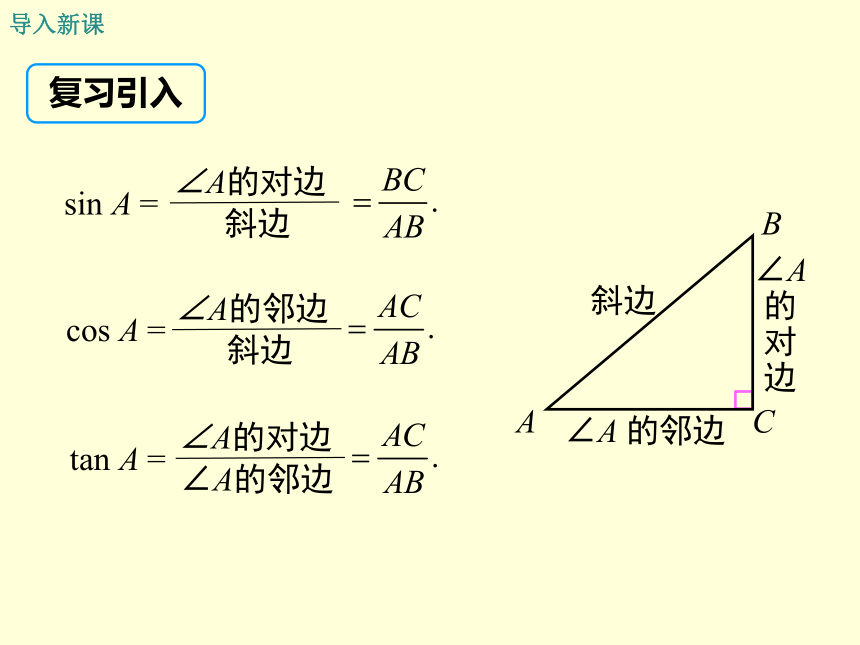
复习引入
A
B
C
∠A 的邻边
∠A
的
对
边
斜边
∠A的对边
斜边
sin A =
∠A的邻边
斜边
cos A =
∠A的对边
∠A的邻边
tan A =
1. 对于sinα与tanα,角度越大,函数值越 ;
对于cosα,角度越大,函数值越 .
2. 互余的两角之间的三角函数关系:
若∠A+∠B=90°,则sinA cosB,cosA sinB,
tanA · tanB = .
大
小
=
=
1
讲授新课
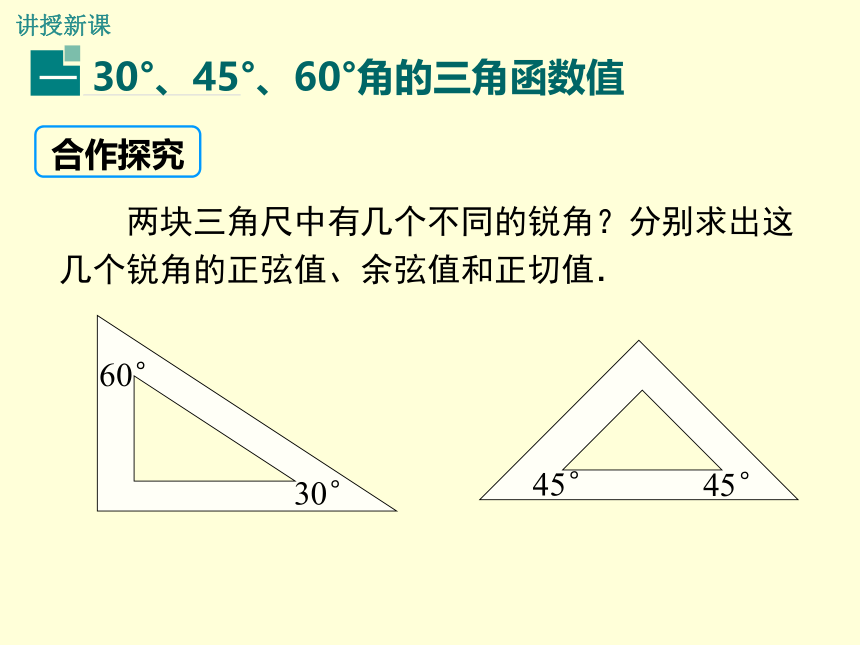
30°、45°、60°角的三角函数值
一
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
60°
45°
45°
合作探究
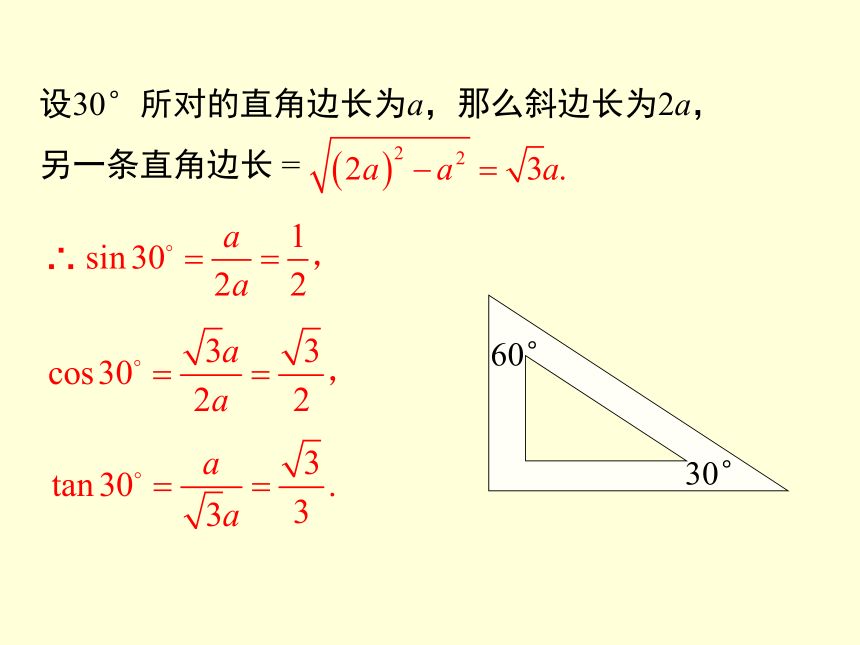
设30°所对的直角边长为a,那么斜边长为2a,
另一条直角边长 =
∴
30°
60°
∴
30°
60°
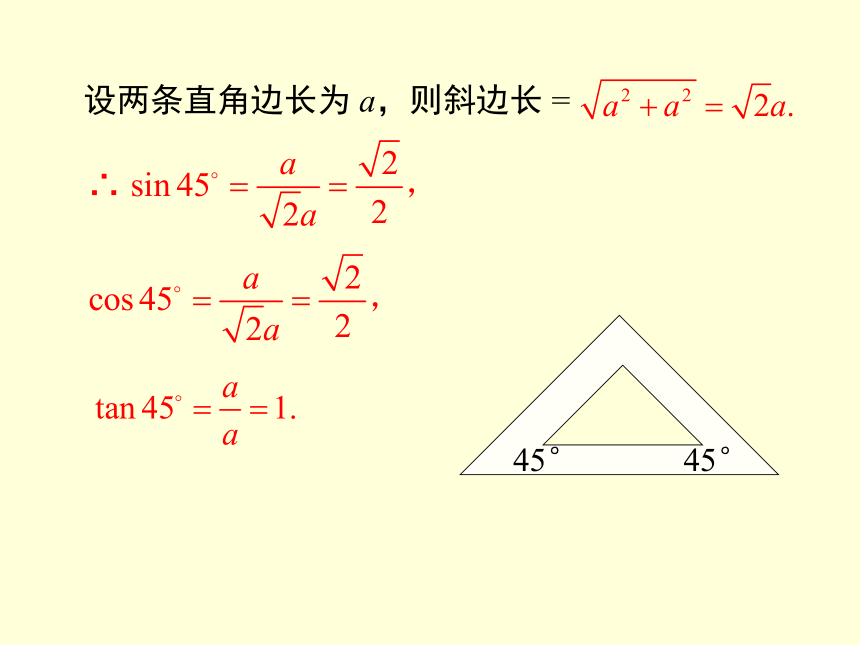
设两条直角边长为 a,则斜边长 =
∴
45°
45°
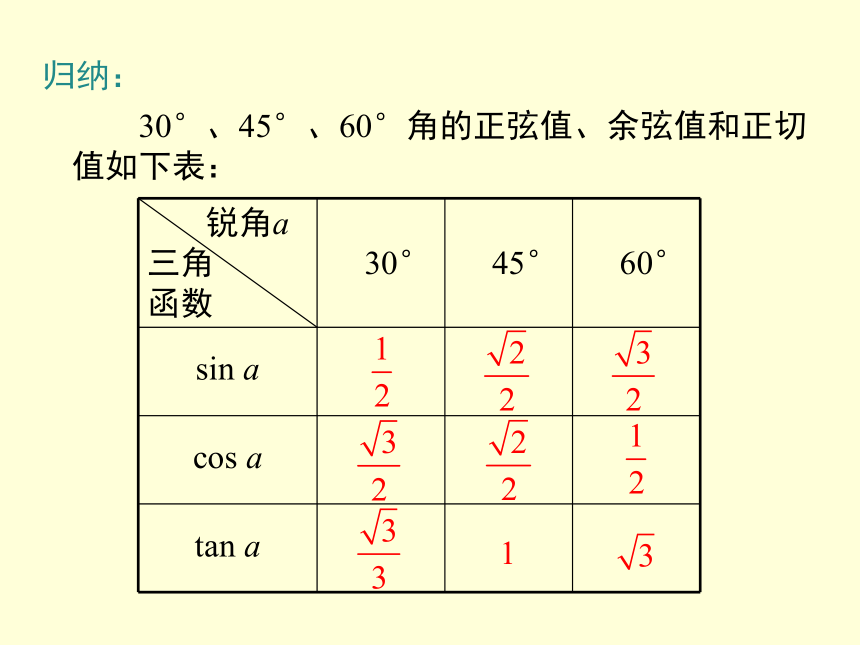
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角
函数
30°
45°
60°
sin a
cos a
tan a
归纳:
1
例1 求下列各式的值:
提示:cos260°表示(cos60°)2,即
(cos60°)×(cos60°).
解:cos260°+sin260°
典例精析
(1) cos260°+sin260°;
(2)
解:
练一练
计算:
(1) sin30°+ cos45°;
解:原式 =
(2) sin230°+ cos230°-tan45°.
解:原式 =
通过三角函数值求角度
二
解: 在图中,
A
B
C
例2 (1) 如图,在Rt△ABC中,∠C = 90°,AB = ,
BC = ,求 ∠A 的度数;
∴ ∠A = 45°.
∵
解: 在图中,
A
B
O
∴ α = 60°.
∵ tanα = ,
(2) 如图,AO 是圆锥的高,OB 是底面半径,AO =
OB,求 α 的度数.
求满足下列条件的锐角 α .
练一练
(1) 2sinα - = 0; (2) tanα-1 = 0.
解:(1) sinα = ,
∴ ∠α = 60°.
(2) tanα =1,
∴ ∠α = 45°.
例3 已知 △ABC 中的 ∠A 与 ∠B 满足 (1-tanA)2 +|sinB- |=0,试判断 △ABC 的形状.
解:∵ (1-tanA)2 + | sinB- |=0,
∴ tanA=1,sinB=
∴ ∠A=45°,∠B=60°,
∠C=180°-45°-60°=75°,
∴ △ABC 是锐角三角形.
当堂练习
1. tan (α+20°)=1,锐角 α 的度数应是 ( )
A.40° B.30° C.20° D.10°
D
A. cosA = B. cosA =
C. tanA = 1 D. tanA =
2. 已知 sinA = ,则下列正确的是 ( )
B
3. 在 △ABC 中,若 ,
则∠C = .
120°
4. 如图,以 O 为圆心,任意长为半径画弧,与射线
OA 交于点 B,再以 B 为圆心,BO 长为半径画弧,
两弧交于点 C,画射线 OC,则 sin∠AOC 的值为
_______.
O
A
B
C
5. 求下列各式的值:
(1) 1-2 sin30°cos30°;
(2) 3tan30°-tan45°+2sin60°;
(3) ;
(4)
答案:(1)
(2)
(3) 2
(4)
7. 如图,在△ABC中,∠A=30°, ,
求 AB的长度.
A
B
C
D
解:过点 C 作 CD⊥AB 于点 D.
∵∠A=30°, ,
∴
A
B
C
D
∴ AB = AD + BD = 3 + 2 = 5.
讲授新课
用计算器求锐角的三角函数值或角的度数
一
例1 (1) 用计算器求sin18°的值;
解:第一步:按计算器 键;
sin
第二步:输入角度值18;
屏幕显示结果 sin18°= 0.309 016 994.
不同计算器操作的步骤可能不同哦!
典例精析
练一练
1. 用计算器求下列各式的值(精确到0.0001):
(1) sin47°;(2) sin12°30′;
(3) cos25°18′;(4) sin18°+cos55°-tan59°.
答案:(1) 0.7314
(2) 0.2164
(3) 0.9041
(4) -0.7817
2. 已知下列锐角三角函数值,用计算器求锐角 ∠A,
∠B的度数 (结果精确到0.1°):
(1) sinA=0.7,sinB=0.01;
(2) cosA=0.15,cosB=0.8;
(3) tanA=2.4,tanB=0.5.
答案:(1) ∠A ≈ 44.4°;∠B ≈ 0.6°.
(2) ∠A ≈ 81.4°;∠B ≈ 36.9°.
(3) ∠A ≈ 67.4°;∠B ≈ 26.6°.
课堂小结
30°、45°、60°角的三角函数值
通过三角函数值求角度
特殊角的三角函数值
利用计算器探索锐三角函数的新知
作业
学思练二
讲授新课
当堂练习
课堂小结
28.1 锐角三角函数
第二十八章 锐角三角函数
第3课时 特殊角的三角函数值
及用计算器求角的三角函数值
学习目标
1. 运用三角函数的知识,自主探索,推导出30°、
45°、60°角的三角函数值. (重点)
2. 会使用科学计算器求锐角的三角函数值.
3. 熟记三个特殊锐角的三角函数值,并能准确地加
以运用. (难点)
导入新课
复习引入
A
B
C
∠A 的邻边
∠A
的
对
边
斜边
∠A的对边
斜边
sin A =
∠A的邻边
斜边
cos A =
∠A的对边
∠A的邻边
tan A =
1. 对于sinα与tanα,角度越大,函数值越 ;
对于cosα,角度越大,函数值越 .
2. 互余的两角之间的三角函数关系:
若∠A+∠B=90°,则sinA cosB,cosA sinB,
tanA · tanB = .
大
小
=
=
1
讲授新课
30°、45°、60°角的三角函数值
一
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
60°
45°
45°
合作探究
设30°所对的直角边长为a,那么斜边长为2a,
另一条直角边长 =
∴
30°
60°
∴
30°
60°
设两条直角边长为 a,则斜边长 =
∴
45°
45°
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角
函数
30°
45°
60°
sin a
cos a
tan a
归纳:
1
例1 求下列各式的值:
提示:cos260°表示(cos60°)2,即
(cos60°)×(cos60°).
解:cos260°+sin260°
典例精析
(1) cos260°+sin260°;
(2)
解:
练一练
计算:
(1) sin30°+ cos45°;
解:原式 =
(2) sin230°+ cos230°-tan45°.
解:原式 =
通过三角函数值求角度
二
解: 在图中,
A
B
C
例2 (1) 如图,在Rt△ABC中,∠C = 90°,AB = ,
BC = ,求 ∠A 的度数;
∴ ∠A = 45°.
∵
解: 在图中,
A
B
O
∴ α = 60°.
∵ tanα = ,
(2) 如图,AO 是圆锥的高,OB 是底面半径,AO =
OB,求 α 的度数.
求满足下列条件的锐角 α .
练一练
(1) 2sinα - = 0; (2) tanα-1 = 0.
解:(1) sinα = ,
∴ ∠α = 60°.
(2) tanα =1,
∴ ∠α = 45°.
例3 已知 △ABC 中的 ∠A 与 ∠B 满足 (1-tanA)2 +|sinB- |=0,试判断 △ABC 的形状.
解:∵ (1-tanA)2 + | sinB- |=0,
∴ tanA=1,sinB=
∴ ∠A=45°,∠B=60°,
∠C=180°-45°-60°=75°,
∴ △ABC 是锐角三角形.
当堂练习
1. tan (α+20°)=1,锐角 α 的度数应是 ( )
A.40° B.30° C.20° D.10°
D
A. cosA = B. cosA =
C. tanA = 1 D. tanA =
2. 已知 sinA = ,则下列正确的是 ( )
B
3. 在 △ABC 中,若 ,
则∠C = .
120°
4. 如图,以 O 为圆心,任意长为半径画弧,与射线
OA 交于点 B,再以 B 为圆心,BO 长为半径画弧,
两弧交于点 C,画射线 OC,则 sin∠AOC 的值为
_______.
O
A
B
C
5. 求下列各式的值:
(1) 1-2 sin30°cos30°;
(2) 3tan30°-tan45°+2sin60°;
(3) ;
(4)
答案:(1)
(2)
(3) 2
(4)
7. 如图,在△ABC中,∠A=30°, ,
求 AB的长度.
A
B
C
D
解:过点 C 作 CD⊥AB 于点 D.
∵∠A=30°, ,
∴
A
B
C
D
∴ AB = AD + BD = 3 + 2 = 5.
讲授新课
用计算器求锐角的三角函数值或角的度数
一
例1 (1) 用计算器求sin18°的值;
解:第一步:按计算器 键;
sin
第二步:输入角度值18;
屏幕显示结果 sin18°= 0.309 016 994.
不同计算器操作的步骤可能不同哦!
典例精析
练一练
1. 用计算器求下列各式的值(精确到0.0001):
(1) sin47°;(2) sin12°30′;
(3) cos25°18′;(4) sin18°+cos55°-tan59°.
答案:(1) 0.7314
(2) 0.2164
(3) 0.9041
(4) -0.7817
2. 已知下列锐角三角函数值,用计算器求锐角 ∠A,
∠B的度数 (结果精确到0.1°):
(1) sinA=0.7,sinB=0.01;
(2) cosA=0.15,cosB=0.8;
(3) tanA=2.4,tanB=0.5.
答案:(1) ∠A ≈ 44.4°;∠B ≈ 0.6°.
(2) ∠A ≈ 81.4°;∠B ≈ 36.9°.
(3) ∠A ≈ 67.4°;∠B ≈ 26.6°.
课堂小结
30°、45°、60°角的三角函数值
通过三角函数值求角度
特殊角的三角函数值
利用计算器探索锐三角函数的新知
作业
学思练二
