人教版数学九年级上册第二十三章《23.2.1 中心对称》课件(共31张PPT)
文档属性
| 名称 | 人教版数学九年级上册第二十三章《23.2.1 中心对称》课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 08:55:55 | ||
图片预览







文档简介
第二十三章 旋转
人教版数学九年级上册
23.2.1 中心对称
学习目标
1.理解中心对称的定义.
2.探究中心对称的性质.
3.掌握中心对称的性质及其应用.
1.旋转的三要素:
旋转中心,旋转方向和旋转角度.
2.旋转的性质:
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
回顾旧知
导入新知
同学们,我们现在研究一类特殊的旋转——中心对称及其性质.
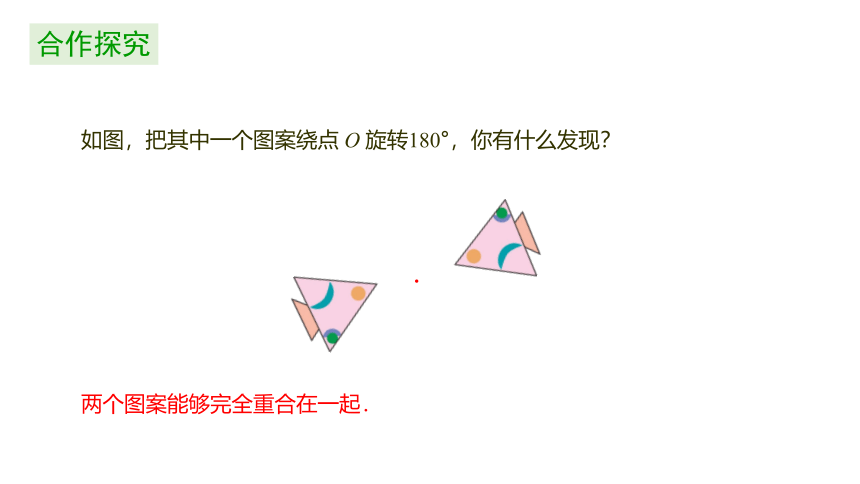
如图,把其中一个图案绕点 O 旋转180°,你有什么发现?
两个图案能够完全重合在一起.
合作探究
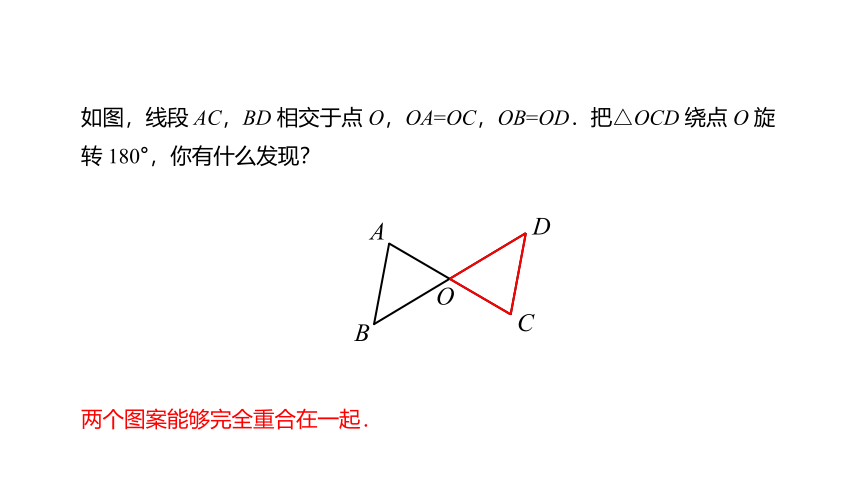
如图,线段 AC,BD 相交于点 O,OA=OC,OB=OD.把△OCD 绕点 O 旋转 180°,你有什么发现?
A
B
D
C
O
两个图案能够完全重合在一起.
你能说说上述两个旋转的共同点吗?
(1)图形中旋转中心是哪一点?
(2)旋转的角度是多少?
(3)两个图形的关系?
点 O
180°
完全重合
如果把一个图形(如△ABO)绕定点O旋转180?,它能够与另一个图形(如△CDO)重合,那么就说这两个图形关于这个点对称或中心对称,这个点就是对称中心.
(1)中心对称是指两个图形间的位置关系,必须涉及两个图形.
(2)中心对称是特殊的旋转,旋转角为180°.
(3)成中心对称的两个图形,只有一个对称中心,这个对称中心可能在两个图形的外部,也可能在图形的内部或图形上,但对称点一定在对称中心的两侧或与对称中心重合.
注意
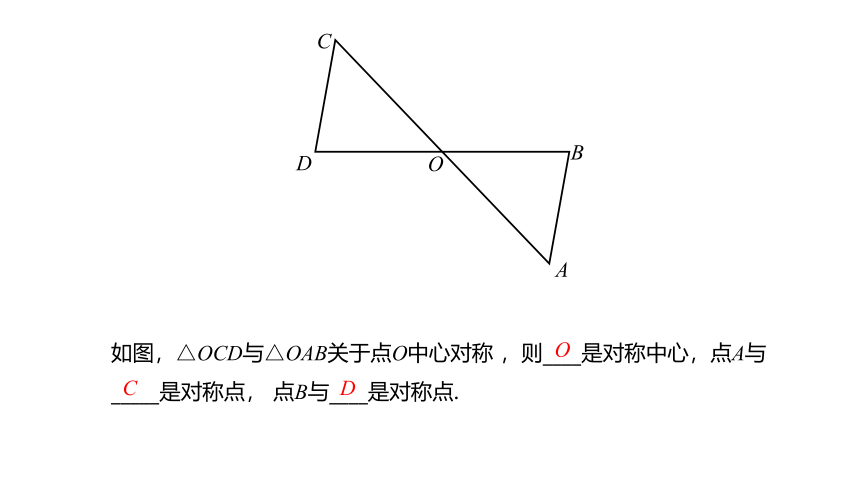
如图,△OCD与△OAB关于点O中心对称 ,则____是对称中心,点A与_____是对称点, 点B与____是对称点.
B
C
A
D
O
O
C
D
1.中心对称是一种特殊的旋转.其旋转角是180 °.
2.中心对称是两个图形之间一种特殊的位置关系.
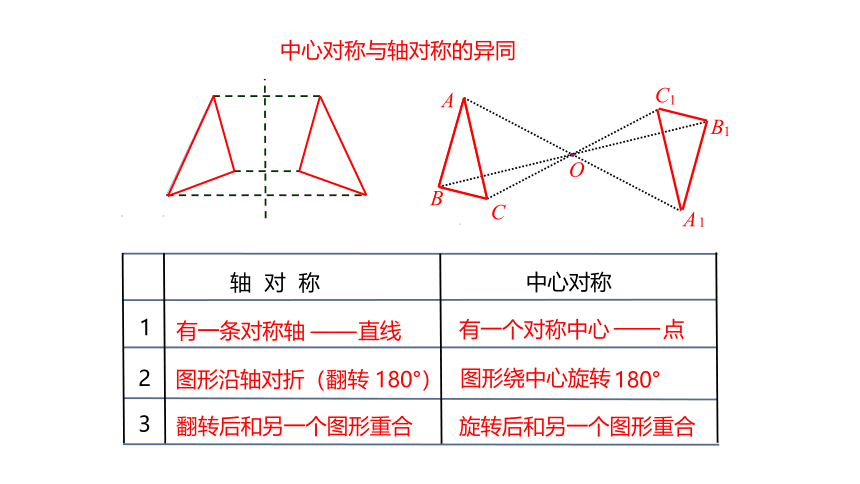
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
如图所示的4组图形中,左边图形与右边图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
C
解:根据中心对称的定义,只有第(4)组图形中的左边图形与右边图形不能形成中心对称.故选C.
(4)
(3)
(2)
(1)
典型例题
下图中△A′B′C′与△ABC关于点O成中心对称,你能从图中找到哪些等量关系?
A′
B′
C′
A
B
C
O
(1) OA=OA′、OB=OB′、 OC=OC′
(2) △ABC≌△A′B′C′
合作探究
如图,旋转三角板,画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为对称中心,把三角板旋转180°,画出△A′B′C′;
第三步,移开三角板.
C
A
B
C
A
B
A′
B′
O
C′
这样画出的△ABC 与△A′B′C′关于点O中心对称,分别连接对称点AA′,BB′,CC′.点O在线段AA′上吗?如果在,在什么位置? △ABC与△A′B′C′有什么关系?
活学巧记
中心对称,平面变换,
对应端点,连线中分,
对应线段,平行相等.
1.成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
2.中心对称的两个图形是全等图形.
中心对称的性质
(1)因为中心对称是一种特殊的旋转变换,所以具备旋转的一切性质.
(2)成中心对称的两个图形,其对应线段互相平行(或在同一条直线上)且相等.
注意
确定对称中心的方法
方法一:连接任意一对对称点,取这条线段的中点,则该点就是对称中心.
方法二:连接任意两对对称点,这两条线段的交点就是对称中心.
1.中心对称的两个图形一定全等,但全等的两个图形不一定成中心对称.
2.用中心对称的性质可以推得线段相等、角相等和图形全等,给几何证明提供了依据.
3.如果两个图形的对应点的连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点中心对称,利用这一性质可以识别中心对称.
如图,△A'B'C'与△ABC关于点O对称,你能从图中找出哪些相等的线段、相等的角、全等的三角形?请举例说明(至少各举三例).
解:本题答案不唯一,如:
相等的线段:OA=OA',OB=OB',OC=OC';
相等的角:∠BAC=∠B'A'C',∠ABC=∠A'B'C',∠ACB=∠A'C'B';
全等的三角形:△ABC≌△A'B'C',△AOC≌△A'OC' ,△BOC≌△B'OC'.
典型例题
图(1)
图(2)
(1)如图(1),选择点O为对称中心,画出点A关于点O的对称点A′;
(2)如图(2),选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
例
合作探究
(1)如图(3),连接AO,在AO的延长线上截取OA′=OA,即可以求得点A
关于点O的对称点A′.
(2)如图(4),作出A,B,C三点关于点O的对称点 A′,B′,C′,依次连
接A′B′,B′C′,C′A′,就可得到与△ABC关于点O对称的△A′B′C′.
图(3)
图(4)
解:
作中心对称的图形的一般步骤:
①确定代表性的点(线段的端点);
②作出每个代表性的点的对称点;
③按照原图形的形状顺次连接各对称点.
如图,已知四边形ABCD和点O,画出四边形ABCD关于点O对称的图形.
A
C
D
B
O
A′
B′
C′
D′
典型例题
1.如图,四边形ABCD是菱形,O是两条对角线的交点,过点O的三条直线将菱形分成六部分.当菱形的两条对角线的长分别为6和8时,阴影部分的面积为 .
12
菱形是中心对称图形,它的两条对角线的交点是对称中心.过点O的三条直线把菱形分成六部分,三块阴影部分和三块空白部分分别对应全等,据此可知阴影部分的面积是菱形面积的一半.
课堂练习
技巧
2.如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).作出△ABC关于原点O对称的△A1B1C1.
A1
B1
C1
?
3.如图,已知在△ABC中,AC=5,AB=3,边BC上的中线AD=2,求BC的长.
1.如果两个图形关于某一点成中心对称,那么下列说法正确的是( )
①对称点的连线必过对称中心;
②这两个图形一定全等;
③对应线段一定平行(或在一条直线上)且相等;
④将一个图形绕对称中心旋转180°必定与另一个图形重合.
A.①② B.①③
C.①②③ D.①②③④
D
中考实题
2.如图(1),在△ABC中,∠A=90° ,D为BC的中点,DE⊥DF, DE交AB于点E,DF交AC于点F,试探索线段BE, EF,FC之间的数量关系.
解:∵D为BC的中点, ∴ BD=CD.
作△BDE关于点D对称的△CDM,如图(2)所示,
由中心对称的性质可得△BDE≌ △CDM.
∴ CM=BE,MD=ED, ∠DCM=∠B.
∵ ∠A=90°,所以∠B+∠ACB=90° ,
∴ ∠DCM+∠ACB=90° ,即∠FCM=90°.
连接FM,在△FME中,MD=DE, FD⊥ME, ∴ FM=EF.
∵在Rt△FCM中,FC2+CM2=FM2,∴FC2+BE2=EF2.
图(1)
图(2)
3.在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系, △ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1 ,并写出点C1的坐标;
解:(1)C1(-1,2).
A1
B1
C1
在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系, △ABC的顶点都在格点上,请解答下列问题:
(2)作出△ABC关于原点O对称的△A2B2C2 ,并写出点C2的坐标.
解:(2) C2(-3,-2).
A2
B2
C2
概念
旋转角是180°
性质
对应点的连线经过对称中心,且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
归纳新知
再 见
人教版数学九年级上册
23.2.1 中心对称
学习目标
1.理解中心对称的定义.
2.探究中心对称的性质.
3.掌握中心对称的性质及其应用.
1.旋转的三要素:
旋转中心,旋转方向和旋转角度.
2.旋转的性质:
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
回顾旧知
导入新知
同学们,我们现在研究一类特殊的旋转——中心对称及其性质.
如图,把其中一个图案绕点 O 旋转180°,你有什么发现?
两个图案能够完全重合在一起.
合作探究
如图,线段 AC,BD 相交于点 O,OA=OC,OB=OD.把△OCD 绕点 O 旋转 180°,你有什么发现?
A
B
D
C
O
两个图案能够完全重合在一起.
你能说说上述两个旋转的共同点吗?
(1)图形中旋转中心是哪一点?
(2)旋转的角度是多少?
(3)两个图形的关系?
点 O
180°
完全重合
如果把一个图形(如△ABO)绕定点O旋转180?,它能够与另一个图形(如△CDO)重合,那么就说这两个图形关于这个点对称或中心对称,这个点就是对称中心.
(1)中心对称是指两个图形间的位置关系,必须涉及两个图形.
(2)中心对称是特殊的旋转,旋转角为180°.
(3)成中心对称的两个图形,只有一个对称中心,这个对称中心可能在两个图形的外部,也可能在图形的内部或图形上,但对称点一定在对称中心的两侧或与对称中心重合.
注意
如图,△OCD与△OAB关于点O中心对称 ,则____是对称中心,点A与_____是对称点, 点B与____是对称点.
B
C
A
D
O
O
C
D
1.中心对称是一种特殊的旋转.其旋转角是180 °.
2.中心对称是两个图形之间一种特殊的位置关系.
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
如图所示的4组图形中,左边图形与右边图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
C
解:根据中心对称的定义,只有第(4)组图形中的左边图形与右边图形不能形成中心对称.故选C.
(4)
(3)
(2)
(1)
典型例题
下图中△A′B′C′与△ABC关于点O成中心对称,你能从图中找到哪些等量关系?
A′
B′
C′
A
B
C
O
(1) OA=OA′、OB=OB′、 OC=OC′
(2) △ABC≌△A′B′C′
合作探究
如图,旋转三角板,画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为对称中心,把三角板旋转180°,画出△A′B′C′;
第三步,移开三角板.
C
A
B
C
A
B
A′
B′
O
C′
这样画出的△ABC 与△A′B′C′关于点O中心对称,分别连接对称点AA′,BB′,CC′.点O在线段AA′上吗?如果在,在什么位置? △ABC与△A′B′C′有什么关系?
活学巧记
中心对称,平面变换,
对应端点,连线中分,
对应线段,平行相等.
1.成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
2.中心对称的两个图形是全等图形.
中心对称的性质
(1)因为中心对称是一种特殊的旋转变换,所以具备旋转的一切性质.
(2)成中心对称的两个图形,其对应线段互相平行(或在同一条直线上)且相等.
注意
确定对称中心的方法
方法一:连接任意一对对称点,取这条线段的中点,则该点就是对称中心.
方法二:连接任意两对对称点,这两条线段的交点就是对称中心.
1.中心对称的两个图形一定全等,但全等的两个图形不一定成中心对称.
2.用中心对称的性质可以推得线段相等、角相等和图形全等,给几何证明提供了依据.
3.如果两个图形的对应点的连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点中心对称,利用这一性质可以识别中心对称.
如图,△A'B'C'与△ABC关于点O对称,你能从图中找出哪些相等的线段、相等的角、全等的三角形?请举例说明(至少各举三例).
解:本题答案不唯一,如:
相等的线段:OA=OA',OB=OB',OC=OC';
相等的角:∠BAC=∠B'A'C',∠ABC=∠A'B'C',∠ACB=∠A'C'B';
全等的三角形:△ABC≌△A'B'C',△AOC≌△A'OC' ,△BOC≌△B'OC'.
典型例题
图(1)
图(2)
(1)如图(1),选择点O为对称中心,画出点A关于点O的对称点A′;
(2)如图(2),选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
例
合作探究
(1)如图(3),连接AO,在AO的延长线上截取OA′=OA,即可以求得点A
关于点O的对称点A′.
(2)如图(4),作出A,B,C三点关于点O的对称点 A′,B′,C′,依次连
接A′B′,B′C′,C′A′,就可得到与△ABC关于点O对称的△A′B′C′.
图(3)
图(4)
解:
作中心对称的图形的一般步骤:
①确定代表性的点(线段的端点);
②作出每个代表性的点的对称点;
③按照原图形的形状顺次连接各对称点.
如图,已知四边形ABCD和点O,画出四边形ABCD关于点O对称的图形.
A
C
D
B
O
A′
B′
C′
D′
典型例题
1.如图,四边形ABCD是菱形,O是两条对角线的交点,过点O的三条直线将菱形分成六部分.当菱形的两条对角线的长分别为6和8时,阴影部分的面积为 .
12
菱形是中心对称图形,它的两条对角线的交点是对称中心.过点O的三条直线把菱形分成六部分,三块阴影部分和三块空白部分分别对应全等,据此可知阴影部分的面积是菱形面积的一半.
课堂练习
技巧
2.如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).作出△ABC关于原点O对称的△A1B1C1.
A1
B1
C1
?
3.如图,已知在△ABC中,AC=5,AB=3,边BC上的中线AD=2,求BC的长.
1.如果两个图形关于某一点成中心对称,那么下列说法正确的是( )
①对称点的连线必过对称中心;
②这两个图形一定全等;
③对应线段一定平行(或在一条直线上)且相等;
④将一个图形绕对称中心旋转180°必定与另一个图形重合.
A.①② B.①③
C.①②③ D.①②③④
D
中考实题
2.如图(1),在△ABC中,∠A=90° ,D为BC的中点,DE⊥DF, DE交AB于点E,DF交AC于点F,试探索线段BE, EF,FC之间的数量关系.
解:∵D为BC的中点, ∴ BD=CD.
作△BDE关于点D对称的△CDM,如图(2)所示,
由中心对称的性质可得△BDE≌ △CDM.
∴ CM=BE,MD=ED, ∠DCM=∠B.
∵ ∠A=90°,所以∠B+∠ACB=90° ,
∴ ∠DCM+∠ACB=90° ,即∠FCM=90°.
连接FM,在△FME中,MD=DE, FD⊥ME, ∴ FM=EF.
∵在Rt△FCM中,FC2+CM2=FM2,∴FC2+BE2=EF2.
图(1)
图(2)
3.在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系, △ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1 ,并写出点C1的坐标;
解:(1)C1(-1,2).
A1
B1
C1
在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系, △ABC的顶点都在格点上,请解答下列问题:
(2)作出△ABC关于原点O对称的△A2B2C2 ,并写出点C2的坐标.
解:(2) C2(-3,-2).
A2
B2
C2
概念
旋转角是180°
性质
对应点的连线经过对称中心,且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
归纳新知
再 见
同课章节目录
