人教版数学九年级上册第二十一章《21.2.1配方法》课件(共18张PPT)
文档属性
| 名称 | 人教版数学九年级上册第二十一章《21.2.1配方法》课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 08:58:02 | ||
图片预览






文档简介
人教版数学九年级上册
第二十一章 二元一次方程
21.2.1 配方法
学习目标
1.初步掌握用直接开平方法解一元二次方程,会用直接开平方法解形如“x2=p或(mx+n)2=p(p≥0)”的方程。
2.会对简单的一元二次方程进行配方。
3.通过对直接开平方法解一元二次方程的学习,进一步了解数学与实际生活的紧密联系。
21.2.1 配方法
解一元二次方程
市区内有一块边长为15米的正方形绿地,经城市规划,需扩大绿化面积,预计规划后的正方形绿地面积将达到300平方米,请问这块绿地的边长增加了多少米?(结果保留一位小数)你能通过一元二次方程解决这个问题吗?
导入新知
解:设这块绿地的边长增加了x米。根据题意得:
(15+x)2=300
?
分类的思想
合作探究
解下列方程:
(2)36x2-1=0.
(1)4x2=81;
?
解:
?
解:
典型例题
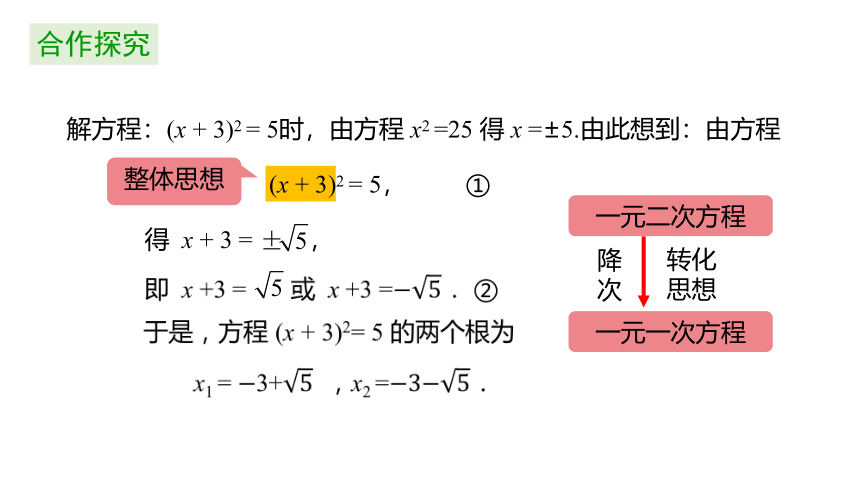
(x + 3)2 = 5, ①
解方程:(x + 3)2 = 5时,由方程 x2 =25 得 x =±5.由此想到:由方程
得 x + 3 = ,
?
?
一元二次方程
降次
转化思想
一元一次方程
整体思想
合作探究
n≥0
?
如何解形式为 (x+m)2=n (其中m,n 是常数)的一元二次方程呢?
n有没有条件限制呢?
?
?
直接开平方法适用于 x2=a (a≥0) 形式的一元二次方程的求解.这里的 x 既可以是字母,单项式,也可以是含有未知数的多项式.
只要经过变形可以转化为 x2=a (a≥0) 形式的一元二次方程都可以用直接开平方法求解.
解下列方程:
(1)(x+5)2=25;
(2)4(x-3)2-32=0.
?
解:
?
解:
典型例题
(1)2x2-8=0;
(2)9x2-5=3;
(3)(x+6)2-9=0;
(4)3(x-1)2-6=0;
(5)x2-4x+4=5;
(6)9x2+5=1.
x=±2
x1=-3,x2=-9
无实数根
?
?
?
1.解下列方程:
课堂练习
2.解下列方程:
(1)3x2-15=0;
(2)(x-1)2-9=0;
(3)(3y+2)2-16=0.
x1=4,x2=-2
?
?
3.用直接开平方法解下列一元二次方程,其中无实数根的方程为( )
A. x2+9=0 B.-2x2=0
C.x2-3=0 D.(x-2)2=0
选项A中,由 x2+9=0 得 x2=-9 ,故方程无实数根,故选A.
解:
A
4.若关于 x 的方程 (x-2)2=a-5 有解,则 a 的取值范围为 .
由题意可得 a-5≥0 ,
所以 a≥5 .
解:
a≥5
5.方程 x2-2=3 的解是 .
?
解:
?
由题意可知 ax2=b 有两个根,
由直接开方法可知:m-1 与 2m+4互为相反数,
所以 m-1 + 2m+4=0,
所以 m= -1,
所以 m-1=-2,2m+4=2,
所以 .
解:
4
再 见
第二十一章 二元一次方程
21.2.1 配方法
学习目标
1.初步掌握用直接开平方法解一元二次方程,会用直接开平方法解形如“x2=p或(mx+n)2=p(p≥0)”的方程。
2.会对简单的一元二次方程进行配方。
3.通过对直接开平方法解一元二次方程的学习,进一步了解数学与实际生活的紧密联系。
21.2.1 配方法
解一元二次方程
市区内有一块边长为15米的正方形绿地,经城市规划,需扩大绿化面积,预计规划后的正方形绿地面积将达到300平方米,请问这块绿地的边长增加了多少米?(结果保留一位小数)你能通过一元二次方程解决这个问题吗?
导入新知
解:设这块绿地的边长增加了x米。根据题意得:
(15+x)2=300
?
分类的思想
合作探究
解下列方程:
(2)36x2-1=0.
(1)4x2=81;
?
解:
?
解:
典型例题
(x + 3)2 = 5, ①
解方程:(x + 3)2 = 5时,由方程 x2 =25 得 x =±5.由此想到:由方程
得 x + 3 = ,
?
?
一元二次方程
降次
转化思想
一元一次方程
整体思想
合作探究
n≥0
?
如何解形式为 (x+m)2=n (其中m,n 是常数)的一元二次方程呢?
n有没有条件限制呢?
?
?
直接开平方法适用于 x2=a (a≥0) 形式的一元二次方程的求解.这里的 x 既可以是字母,单项式,也可以是含有未知数的多项式.
只要经过变形可以转化为 x2=a (a≥0) 形式的一元二次方程都可以用直接开平方法求解.
解下列方程:
(1)(x+5)2=25;
(2)4(x-3)2-32=0.
?
解:
?
解:
典型例题
(1)2x2-8=0;
(2)9x2-5=3;
(3)(x+6)2-9=0;
(4)3(x-1)2-6=0;
(5)x2-4x+4=5;
(6)9x2+5=1.
x=±2
x1=-3,x2=-9
无实数根
?
?
?
1.解下列方程:
课堂练习
2.解下列方程:
(1)3x2-15=0;
(2)(x-1)2-9=0;
(3)(3y+2)2-16=0.
x1=4,x2=-2
?
?
3.用直接开平方法解下列一元二次方程,其中无实数根的方程为( )
A. x2+9=0 B.-2x2=0
C.x2-3=0 D.(x-2)2=0
选项A中,由 x2+9=0 得 x2=-9 ,故方程无实数根,故选A.
解:
A
4.若关于 x 的方程 (x-2)2=a-5 有解,则 a 的取值范围为 .
由题意可得 a-5≥0 ,
所以 a≥5 .
解:
a≥5
5.方程 x2-2=3 的解是 .
?
解:
?
由题意可知 ax2=b 有两个根,
由直接开方法可知:m-1 与 2m+4互为相反数,
所以 m-1 + 2m+4=0,
所以 m= -1,
所以 m-1=-2,2m+4=2,
所以 .
解:
4
再 见
同课章节目录
