人教版数学九年级下册27.3 位似——两个位似图形坐标之间的关系课件(共18张ppt)
文档属性
| 名称 | 人教版数学九年级下册27.3 位似——两个位似图形坐标之间的关系课件(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 09:24:39 | ||
图片预览



文档简介
27.3 位 似
第2课时
1.什么叫位似图形?
2.利用位似可以把一个图形放大或缩小.
如果两个图形的对应顶点的连线都经过同一点O,且这点与对应顶点所连线段成比例,那么这两个图形叫做位似图形.点O是位似中心.
D
E
F
A
O
B
C
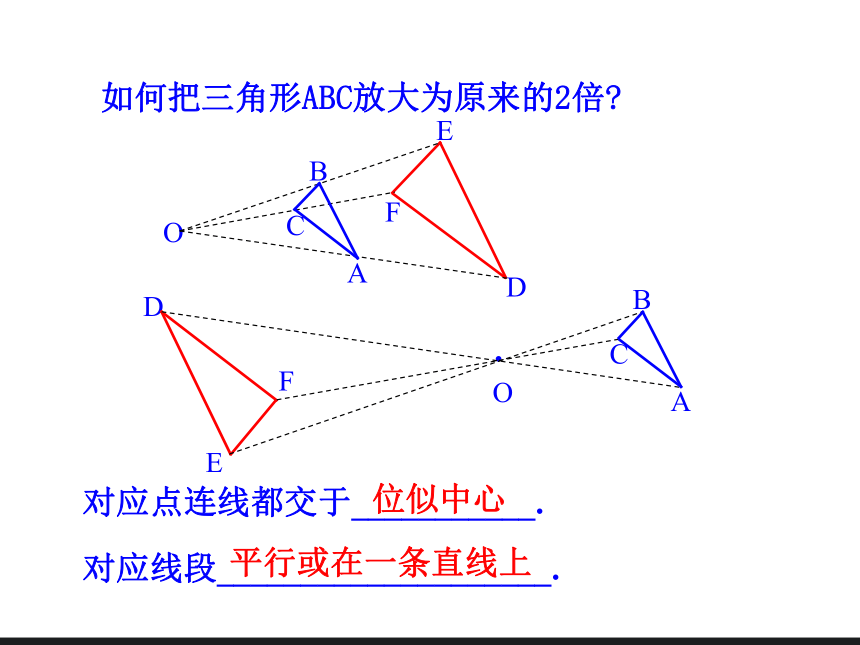
如何把三角形ABC放大为原来的2倍?
D
E
F
A
.O
B
C
对应点连线都交于___________.
对应线段____________________.
位似中心
平行或在一条直线上
1.会用图形的坐标的变化来表示图形的位似变换,掌握把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律.
2.了解四种变换(平移、轴对称、旋转和位似)的异同,并能在复杂图形中找出这些变换.
B'
A'
x
y
B
A
o
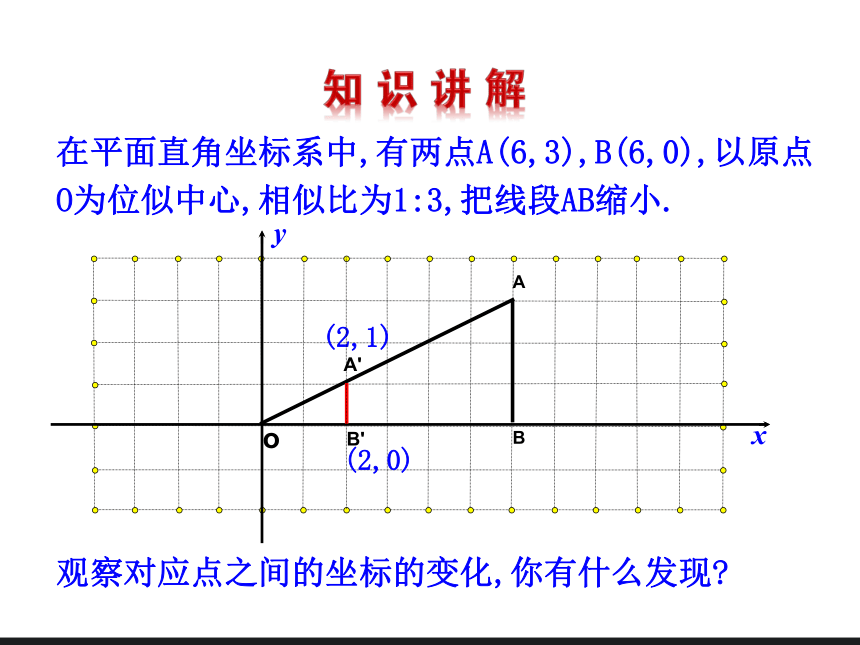
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
(2,1)
观察对应点之间的坐标的变化,你有什么发现?
(2,0)
B'
A'
x
y
B
A
o
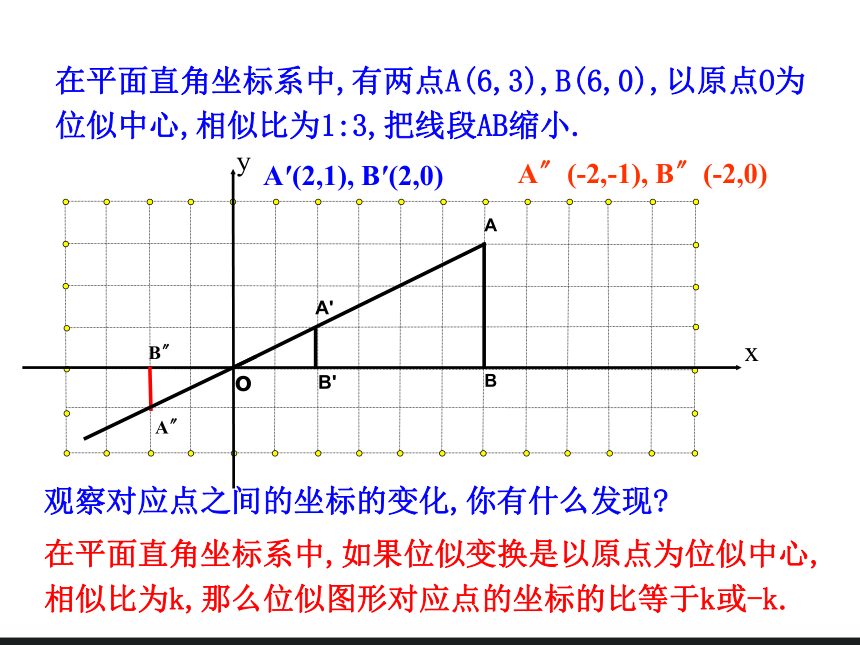
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1), B′(2,0)
A〞
B〞
A〞(-2,-1), B〞(-2,0)
在平面直角坐标系中,如果位似变换是以原点为位似中心,
相似比为k,那么位似图形对应点的坐标的比等于k或-k.
观察对应点之间的坐标的变化,你有什么发现?
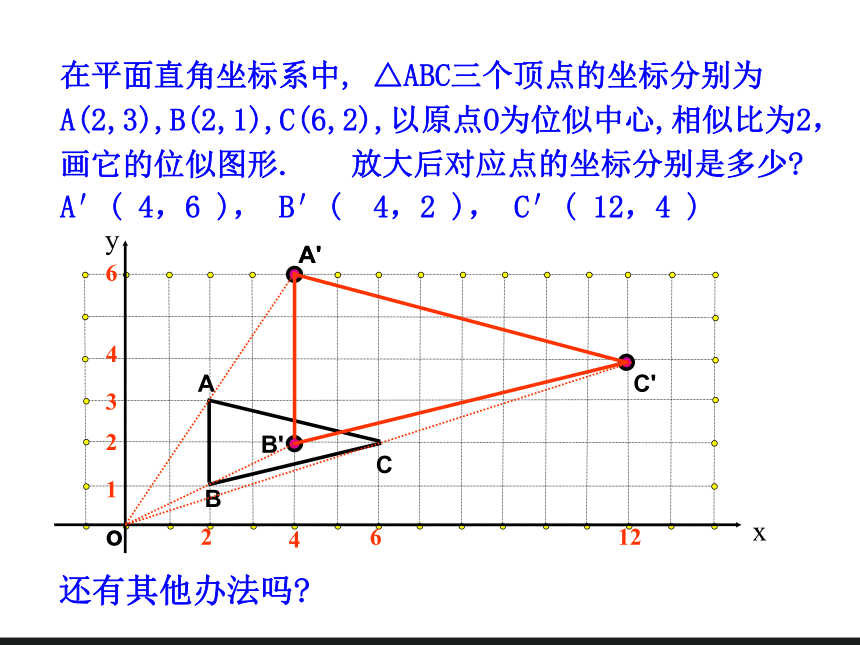
在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2,画它的位似图形.
A′( 4,6 ), B′( 4,2 ), C′( 12,4 )
放大后对应点的坐标分别是多少?
A'
x
y
o
B
A
C
B'
A'
C'
还有其他办法吗?
2
4
6
12
1
3
6
2
4
在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1), C(6,2),以原点O为位似中心,相似比为2,将△ABC放大.
A〞( -4 ,-6 ), B〞( -4 ,-2 ), C〞( -12 ,-4 )
放大后对应点的坐标分别是多少?
x
y
o
B
A
C
B〞
A〞
C〞
【例】在平面直角坐标系中, 四边形ABCD的四个顶点
的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画
出它的一个以原点O为位似中心,相似比为 的位似图
形.
例题讲解
x
y
o
A′(-3,3), B′(-4,1), C′(-2,0), D′(-1,2)
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗?试试看.
x
y
o
B
如图,表示△AOB和把它缩小后得到的△COD,则它们
的相似比为 .
A
C
D
5:2
当堂训练
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在如图所示的图案中,你能找到这些变换吗?
注:图形的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.
轴对称
对称轴
平移
平移的方向,平移的距离.
旋转
旋转中心,旋转方向,旋转角度.
位似
位似中心、位似比.
在平面直角坐标系中,如果位似变换是以原点
为位似中心,相似比(新图与原图的相似比)为k,
那么位似图形对应点的坐标的比等于k或-k,则图像
上的对应点的坐标为(kx,ky)或(-kx,-ky)。
1.如图,将△ABC的三边分别扩大一倍得到△A1B1C1(顶点均在格点上),它们是以P点为位似中心的位似图形,则P点的坐标是( )
A.(―4,―3) B.(―3,―3)
C.(―4,―4) D.(―3,―4)
答案: 选A.
当堂检测
2.关于对位似图形的表述,下列命题正确
的是 .(只填序号)
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的
直线都经过同一个点,那么,这两个图形是位似图形;
④位似图形上任意两点与位似中心的距离之比等于相似
比.
答案:②③
3.两个位似图形中的对应角______,对应线段的比_____,
对应顶点的连线必经过__________.
4.位似图形上某一对对应点到位似中心的距离分别为5和
10,则它们的相似比为______.
5.四边形ABCD和四边形A′B′C′D′位似,O为位似中
心,若OA:OA′=1:4,那么S四边形ABCD :S四边形A′B′C′D′
=_____.
相等
位似中心
相等
1:2
1:16
作业布置:
课本P51第3,5题
第2课时
1.什么叫位似图形?
2.利用位似可以把一个图形放大或缩小.
如果两个图形的对应顶点的连线都经过同一点O,且这点与对应顶点所连线段成比例,那么这两个图形叫做位似图形.点O是位似中心.
D
E
F
A
O
B
C
如何把三角形ABC放大为原来的2倍?
D
E
F
A
.O
B
C
对应点连线都交于___________.
对应线段____________________.
位似中心
平行或在一条直线上
1.会用图形的坐标的变化来表示图形的位似变换,掌握把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律.
2.了解四种变换(平移、轴对称、旋转和位似)的异同,并能在复杂图形中找出这些变换.
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
(2,1)
观察对应点之间的坐标的变化,你有什么发现?
(2,0)
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1), B′(2,0)
A〞
B〞
A〞(-2,-1), B〞(-2,0)
在平面直角坐标系中,如果位似变换是以原点为位似中心,
相似比为k,那么位似图形对应点的坐标的比等于k或-k.
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2,画它的位似图形.
A′( 4,6 ), B′( 4,2 ), C′( 12,4 )
放大后对应点的坐标分别是多少?
A'
x
y
o
B
A
C
B'
A'
C'
还有其他办法吗?
2
4
6
12
1
3
6
2
4
在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1), C(6,2),以原点O为位似中心,相似比为2,将△ABC放大.
A〞( -4 ,-6 ), B〞( -4 ,-2 ), C〞( -12 ,-4 )
放大后对应点的坐标分别是多少?
x
y
o
B
A
C
B〞
A〞
C〞
【例】在平面直角坐标系中, 四边形ABCD的四个顶点
的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画
出它的一个以原点O为位似中心,相似比为 的位似图
形.
例题讲解
x
y
o
A′(-3,3), B′(-4,1), C′(-2,0), D′(-1,2)
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗?试试看.
x
y
o
B
如图,表示△AOB和把它缩小后得到的△COD,则它们
的相似比为 .
A
C
D
5:2
当堂训练
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在如图所示的图案中,你能找到这些变换吗?
注:图形的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.
轴对称
对称轴
平移
平移的方向,平移的距离.
旋转
旋转中心,旋转方向,旋转角度.
位似
位似中心、位似比.
在平面直角坐标系中,如果位似变换是以原点
为位似中心,相似比(新图与原图的相似比)为k,
那么位似图形对应点的坐标的比等于k或-k,则图像
上的对应点的坐标为(kx,ky)或(-kx,-ky)。
1.如图,将△ABC的三边分别扩大一倍得到△A1B1C1(顶点均在格点上),它们是以P点为位似中心的位似图形,则P点的坐标是( )
A.(―4,―3) B.(―3,―3)
C.(―4,―4) D.(―3,―4)
答案: 选A.
当堂检测
2.关于对位似图形的表述,下列命题正确
的是 .(只填序号)
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的
直线都经过同一个点,那么,这两个图形是位似图形;
④位似图形上任意两点与位似中心的距离之比等于相似
比.
答案:②③
3.两个位似图形中的对应角______,对应线段的比_____,
对应顶点的连线必经过__________.
4.位似图形上某一对对应点到位似中心的距离分别为5和
10,则它们的相似比为______.
5.四边形ABCD和四边形A′B′C′D′位似,O为位似中
心,若OA:OA′=1:4,那么S四边形ABCD :S四边形A′B′C′D′
=_____.
相等
位似中心
相等
1:2
1:16
作业布置:
课本P51第3,5题
